Interpretation of Slope and Y-Intercept
With the exception of the vertical line which has the equation x = k, where k is a number, the equation of a line always has the form y = mx + b.
Example 1. 
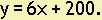
Two important facts are contained in this equation.
a) The slope of the line is 6, which means that y increases by 6 units whenever x increases by 1 unit.
b) The y-intercept for the line is (0, 200), which means that the line crosses the y-axis at this point and that y = 200 when x = 0.
Here are some possible interpretations of the equation in the previous example.
Suppose that in the above example, y represents the cost of manufacturing x units of some product. This equation tells us that every unit manufactured raises the total cost by $6; and that, even when no units are manufactured, the cost of doing business is $200. The $200 is called the fixed cost.
Suppose that in the above example, y represents the height of a shrub measured in cm, and x represents the number of years since the shrub was planted. The equation tells us that the shrub is growing at the rate of 6 cm per year, and that the height of the shrub when it was planted was 200 cm.
Suppose that in the above example, y is the number of gallons of water in a pool, and x is the number of hours since a water supply flowing into the pool was turned on. We know that the pool is filling at the rate of 6 gallons per hour, and that the pool contained 200 gallons when the faucet was turned on. If the pool will hold 500 gallons, we can calculate how many hours it will take to fill it by solving the equation 500 = 6x + 200.
Example 2. 
The available information is:
a) The slope is -3, which means that y decreases by 3 units each time x increases by one unit.
b) The y-intercept is the point (0, 60), which means that the line crosses the y-axis at this point.
In Example 2, if y represents the number of quarts of water in a tub, and x represents the number of minutes since a drain was opened, the equation tells us that the water is draining out at the rate of 3 quarts per minute, and that the tub contained 60 quarts of water when the drain was opened. To find how long it takes to drain the tub, we solve the equation 0 = -3x + 60 to find that the answer is 20 minutes.
Example 3. Suppose that the monthly salary in dollars earned by a salesperson is given by the equation 
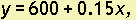where x represents the total sales by that person for the month measured in dollars.
The information available here is that the salesperson earns 15% of all sales for the month, and that the salary would be $600 even with no sales for the month.
Monthly sales of $6,000 would yield a salary of 600 + 0.15(6,000) or $1,500 for the salesperson. The slope of the line is the commission rate for the salesperson.