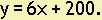
With the exception of the vertical line which has the equation x = k, where k is a number, the equation of a line always has the form y = mx + b.
Example 1.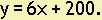
Two important facts are contained in this equation.
a) The slope of the line is 6, which means that y increases by 6 units whenever x increases by 1 unit.
b) The y-intercept for the line is (0, 200), which means that the line crosses the y-axis at this point and that y = 200 when x = 0.
Here are some possible interpretations of the equation in the previous example.
Suppose that in the above example, y represents the cost of manufacturing x units of some product. This equation tells us that every unit manufactured raises the total cost by $6; and that, even when no units are manufactured, the cost of doing business is $200. The $200 is called the fixed cost.
Suppose that in the above example, y represents the height of a shrub measured in cm, and x represents the number of years since the shrub was planted. The equation tells us that the shrub is growing at the rate of 6 cm per year, and that the height of the shrub when it was planted was 200 cm.
Suppose that in the above example, y is the number of gallons of water in a pool, and x is the number of hours since a water supply flowing into the pool was turned on. We know that the pool is filling at the rate of 6 gallons per hour, and that the pool contained 200 gallons when the faucet was turned on. If the pool will hold 500 gallons, we can calculate how many hours it will take to fill it by solving the equation 500 = 6x + 200.
Example 2. 
The available information is:
a) The slope is -3, which means that y decreases by 3 units each time x increases by one unit.
b) The y-intercept is the point (0, 60), which means that the line crosses the y-axis at this point.
In Example 2, if y represents the number of quarts of water in a tub, and x represents the number of minutes since a drain was opened, the equation tells us that the water is draining out at the rate of 3 quarts per minute, and that the tub contained 60 quarts of water when the drain was opened. To find how long it takes to drain the tub, we solve the equation 0 = -3x + 60 to find that the answer is 20 minutes.
Example 3. Suppose that the monthly salary in dollars earned by a salesperson is given by the equation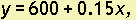 
where x represents the total sales by that person for the month measured in dollars.
The information available here is that the salesperson earns 15% of all sales for the month, and that the salary would be $600 even with no sales for the month.
Monthly sales of $6,000 would yield a salary of 600 + 0.15(6,000) or $1,500 for the salesperson. The slope of the line is the commission rate for the salesperson.
Information may also be gained from the graph of an equation as shown in the following examples:
Example 4. Use the graph shown below to answer the questions.
a) Find the value of y when x = 4.
b) Find the value of x when y = 4.
c) Find the slope of the line.
d) Find the y-intercept for the line.
e) Find the x-intercept for the line.
Answers:
a) y = 6
b) x = 3
c) 2
d) (0,-2)
e) (1,0)
Example 5. Using the graph given in the previous example, assume that x represents the number of years that a company has been in business, and that y represents the total profit of the company for that year measured in hundreds of thousands of dollars.
Answer the following questions.
a) What portion of the graph would need to be deleted to make it realistically describe the situation described above?
b) What would be the amount of profit for the company the third year it was in business?
c) By what amount is profit increasing each year?
Answers:
a) Anything in second or third quadrant
b) 4 hundred thousand dollars
c) 2 hundred thousand dollars
Example 6. Use the graph below to answer the questions which follow.
a) Find y when x = 5.
b) Find the amount y changes when x increases by 3.
c) Find the x-intercept for the line.
d) Find the y-intercept for the line.
Answers:
a) y = 2
b) none
c) none
d) (0,2)
Please view the following video:
The lines having the simplest equations are the vertical and the horizontal lines.
Vertical Lines
The equation of any vertical line (whose slope is undefined) is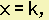 
where k is the x-coordinate of every point on the line.
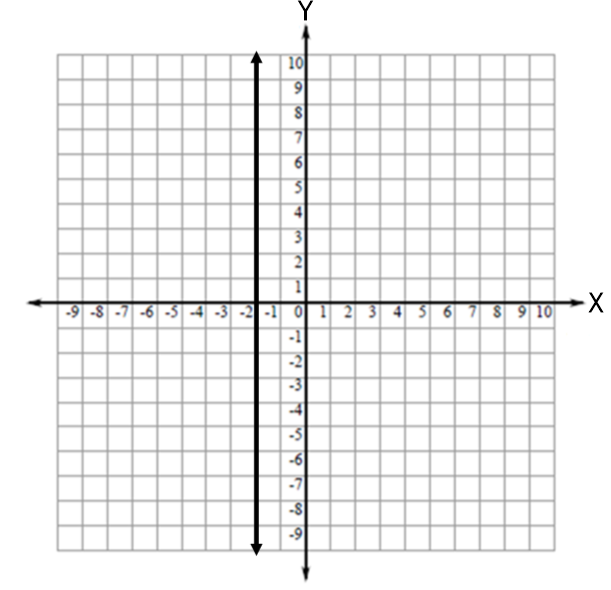
Example 7. Find the equation of the line graphed above:
Answer:
Since the line is vertical and every point has x-coordinate -2, the equation is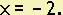 
Example 8. Find the equation of the line through the points (2,-3) and (2,4).
Answer:
Since one of these points lies directly above the other, the line is vertical and thus has the equation 
Note that the slope cannot be computed for this line.
Example 9. Find the equation of the line whose slope is undefined and which passes through the point (6, 0).
Answer:
The line is vertical since its slope is undefined. Its equation is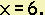 
From the section on slope, we have seen that the slope of a horizontal line is zero. Look at the graph of the horizontal line below:
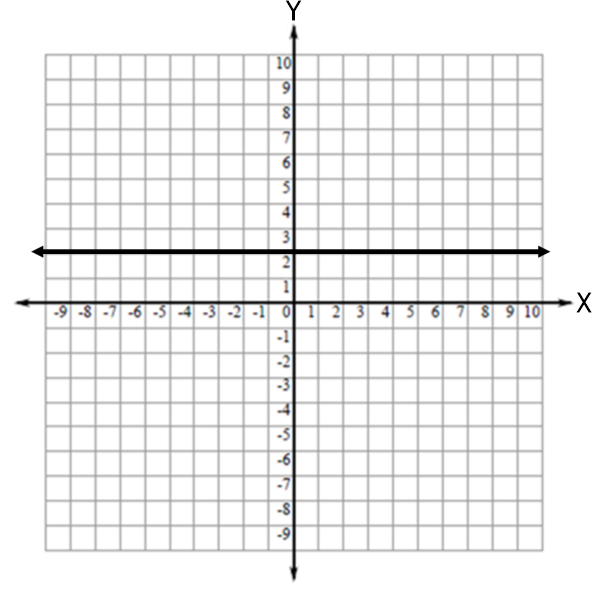
If we list a few of the points that are on the horizontal line shown above such as (-4, 2), (-2, 2), (0, 2), (2, 2), (4, 2), etc., we see that every point has a y-coordinate of 2.
The equation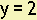 
completely describes the line, because y is 2 for any value of x. Because this line is horizontal, the value of x can be any number, but the value of y is always 2.
The equation of any horizontal line (whose slope is zero) is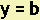 
, where b is the y-coordinate of every point on the line.
Example 10. Write the equation of the line shown above:
Answer:
The equation is 
because every point on the line has a y-coordinate of -3.
Example 11. Write the equation of the line which has slope of zero and passes through the point (3, 16).
Answer:
A slope of zero means that the line is horizontal. The line has the equation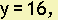 
because it must pass through the point (3, 16).
Please view the following videos:
Most applications of lines involve lines which are neither vertical nor horizontal. Every line which is not vertical can be written in the form
where m is the slope of the line, and the number b is the y-intercept of the line. This form of the equation of a line is called the slope-intercept equation of a line. The y-intercept is the point where the line crosses the y-axis. The x-coordinate of the y-intercept of a graph is always zero.
Example 12. Find the equation of the line having slope 5 and passing through the point (0,2).
Answer:
y = 5x + b
2 = 5(0) + b replacing y with 2 and x with 0 to find b.
2 = b
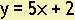
Example 13. Find the equation of the line having slope 7 and passing through the point (2,9).
Answer:
y = 7x + b
9 = 7(2) + b replacing x with 2 and y with 9.
9 = 14 + b
-5 = b
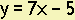
Example 14. Find the equation of the line with slope -4 and passing through the point (-1,2).
Answer:
y = -4x + b
2 = -4(-1) + b
2 = 4 + b
-2 = b
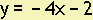
Please view the following videos:
Your calculator will calculate the slope and the y-intercept given any two points on the line. However, your calculator uses the letter a for the letter m. Hence, the equation of the line is y = ax + b. On the TI-30XS MultiView calculator, you calculate a and b as follows:
To enter the two points (2, 7) and (5, 13) into the calculator:
1. Press 
(twice).
2. Arrow down to highlight 4: Clear All.
3. Press 
to clear out any data that is left over from a previous problem.
4. Enter the x values of each point in L1 and the y values of each point in L2 using the arrow keys to move between the two columns.
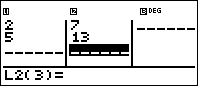
5. Press 
. (The word stat is above the 
key)
6. Arrow down to highlight: 2: 2-Var Stats
7. Press
8. For xDATA highlight L1
9. Press
10. For yDATA highlight L2
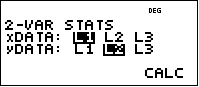
11. Press
12. Arrow down to highlight CALC
13. Press
14. Arrow down several times to highlight D: a=2
15. Arrow down once more to highlight E: b=3
16. Once you determine the values of a and b, write the equation in the form y = ax + b. In this example, the equation of the line is y = 2x + 3.
Example 15. Use your calculator to find the equation of the line through the points (2, 7) and (5, 13).
Answer: 
Example 16. Use your calculator to find the equation of the line that passes through (-2, -3) and (-4, -5).
Answer: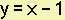 
Example 17. Find the equation of the line with slope 2.5 and having a y-intercept of (0, 4).
Answer: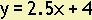 
Please view the following video:
Example 18. A shrub is 20 cm tall when it is planted, and it grows 4 cm each week for the next 15 weeks. Assuming that the equation is a straight line, write the equation relating y,the height of the shrub in cm, to x, the number of weeks since it was planted.
Answer:
The slope of the line is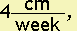 
since this is the amount the height increases for each additional week of time. Since the shrub is 20 cm tall when it is planted, this means that y = 20 when x = 0. In other words, the y-intercept is (0, 20).
Using the formula y = mx + b, the equation is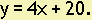 
Example 19. If the value of a piece of machinery when it is purchased is $30,000, and it is worth $10,000 five years later, find the equation relating its value, y, to its age, x, assuming that the equation is a line.
Answer:
When the age, x, of the machinery is 0, its value, y, is $30,000; and when the age is 5 years, the value is $10,000. These data correspond to the points (0, 30,000) and (5, 10,000). Using the calculator, we obtain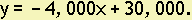 
Notice that the slope in example 18 is positive, since the height of the shrub increases as its age increases; whereas in example 19, the slope is negative, since the value of the machinery decreases as its age increases.
Example 20. To take the previous problem further, find the value of the machinery 7 years after it is purchased.
Answer:
Substitute 7 into the formula for x giving
y = -4,000(7) + 30,000
y = -28,000 + 30,000
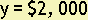
This equation tells you that the machinery is worth $2,000 seven years after it is purchased. This situation where an object loses the same amount of value each year is called straight-line depreciation.
Example 21:
Referring to the following table for XYZ Company, what would be the equation of the line?
|
XYZ Company |
Units Sold |
Shipping Expense |
|
High activity level |
15,000 |
$75,000 |
|
Low activity level |
5000 |
$35,000 |
Answer:
Let y represent the shipping expense.
Let x represent the number of units sold.
Let a represent the variable cost rate of the shipping expense.
Let b represent the fixed cost of the shipping expense.
The equation of the line would be in the form y = ax + b. Thus, Total Shipping Expense = Variable Cost Rate times the number of units sold + Fixed Cost.
The variable cost rate is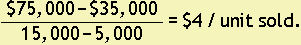 
Using the fact that when 15,000 units is sold the shipping expense is $75,000, we have
$75,000 = $4.00 x 15,000 + b
$75,000 = $60,000 + b
$15,000 = b
Equation of the line: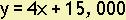 
Please view the following video:
Click on the following links to access:
Practice Homework Problems
Graph Paper for Working Practice Homework Problems