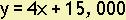Example 18. A shrub is 20 cm tall when it is planted, and it grows 4 cm each week for the next 15 weeks. Assuming that the equation is a straight line, write the equation relating y,the height of the shrub in cm, to x, the number of weeks since it was planted.
Answer:
The slope of the line is 
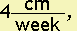since this is the amount the height increases for each additional week of time. Since the shrub is 20 cm tall when it is planted, this means that y = 20 when x = 0. In other words, the y-intercept is (0, 20).
Using the formula y = mx + b, the equation is 
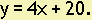
Example 19. If the value of a piece of machinery when it is purchased is $30,000, and it is worth $10,000 five years later, find the equation relating its value, y, to its age, x, assuming that the equation is a line.
Answer:
When the age, x, of the machinery is 0, its value, y, is $30,000; and when the age is 5 years, the value is $10,000. These data correspond to the points (0, 30,000) and (5, 10,000). Using the calculator, we obtain 
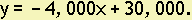
Notice that the slope in example 18 is positive, since the height of the shrub increases as its age increases; whereas in example 19, the slope is negative, since the value of the machinery decreases as its age increases.
Example 20. To take the previous problem further, find the value of the machinery 7 years after it is purchased.
Answer:
Substitute 7 into the formula for x giving
y = -4,000(7) + 30,000
y = -28,000 + 30,000
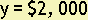
This equation tells you that the machinery is worth $2,000 seven years after it is purchased. This situation where an object loses the same amount of value each year is called straight-line depreciation.
Example 21:
Referring to the following table for XYZ Company, what would be the equation of the line?
|
XYZ Company |
Units Sold |
Shipping Expense |
|
High activity level |
15,000 |
$75,000 |
|
Low activity level |
5000 |
$35,000 |
Answer:
Let y represent the shipping expense.
Let x represent the number of units sold.
Let a represent the variable cost rate of the shipping expense.
Let b represent the fixed cost of the shipping expense.
The equation of the line would be in the form y = ax + b. Thus, Total Shipping Expense = Variable Cost Rate times the number of units sold + Fixed Cost.
The variable cost rate is 
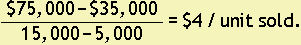Using the fact that when 15,000 units is sold the shipping expense is $75,000, we have
$75,000 = $4.00 x 15,000 + b
$75,000 = $60,000 + b
$15,000 = b
Equation of the line: 