At the time when I began to write this article (August 2014), the media were very keen to tell us that we had just experienced what they called a "Supermoon": a Full Moon that was much bigger and brighter than usual. These, they said, occurred every 13 months and were as a result of the Moon being much nearer to the Earth. In consequence, the Moon would be 14% larger and 30% brighter. However, I had serious doubts about the "every 13 months" assertion at the very least, so I decided to check all the above "facts". As usual, this turned out to be more complicated than expected!
The part of the media reports that is basically correct is the bit about a Supermoon being nearer to the Earth. The path of the Moon round the Earth is decidedly elliptical rather than circular and so the Moon is sometimes nearer to the Earth than average and at other times it is farther away. The nearest point on a given orbit is called "perigee" [from the Greek for "near to Earth"] and the most distant point is called "apogee" ["far from Earth"]. As with any object, heavenly or not, when the Moon is nearer to us it appears to be larger. Its path is strongly perturbed by the Sun though and so each orbit is somewhat different from those before and after. In particular, the degree to which it is non-circular (its "eccentricity") varies quite a lot, which affects the perigee and apogee distances. So, although the mean perigee distance is 363296km, calculation using lunar orbital theory shows it varying from 356445km to 370354km in the 80 years between 1960 and 2040. Over the extended period 1500BC to 8000AD its absolute minimum value is 356353km. Not all Supermoons are created equal, therefore! However, even in the "best case scenario" of a Full Moon coinciding with a minimum-distance perigee its apparent diameter will be just 7.87% larger than average (the ratio of the distances) and therefore, in principle, it will be 16.4% brighter (as brightness is inversely proportional to the square of the distance): what I mean by "in principle" will become apparent much further on in this article! These numbers are considerably smaller than the figures quoted by the media, but it is easy to show that the "media" values actually refer to the increased size and brightness of a best-case Supermoon relative not to the average but to the absolute smallest size a Full Moon can be, which is attained when it is at its greatest possible apogee distance of 406720km. The commonly-quoted figures are, therefore, something of a cheat.
However, all these numbers take no account of the fact that we are observing the Moon from the surface of the Earth rather than its centre (from where orbital distances are measured) nor of the variation in the Sun-to-Earth/Moon distance due to the eccentricity of the Earth's orbit, which will affect the amount of sunlight falling on the Moon in the first place. The former only makes a small difference, making the numbers 8.01% larger and 16.7% brighter rather than 7.87% and 16.4%, but the latter makes a considerable difference so that when both factors are combined a best-case Supermoon at perihelion (the point at which the Earth is closest to the Sun) will, again in principle, be 20.7% brighter than an average Full Moon.
As well as reporting the increase in size and brightness, there is also the implication in the media that a Supermoon is dramatically different from other Full Moons i.e. that its size and brightness set it notably apart from the norm. In fact, both the size and the brightness of Full Moons span a continuous range. There is no "gap" separating Supermoons from "normal" Full Moons, it's simply that the name "Supermoon" is given to those at the extreme end of the spectrum. Thus if we define a Supermoon as one which is 20% brighter than average, there will be Full Moons almost identical to it but which are "only" 19.9% brighter and so are "non-Super". The definition of a Supermoon in terms of its distance, its size or its brightness is therefore purely arbitrary: the number of "media Supermoons" thus depends entirely on where one draws the line, not on any inherent feature of the Moon's orbital mechanics.
However, despite the fact that actuality is rather less than the populist hype, there really is a significant increase in both size and brightness relative to an average Full Moon, and so one would surely still expect a Supermoon to look quite spectacular? Well no, not really. While the change in size would be easily apparent if one compared, side-by-side, pictures taken of a Supermoon and a "normal" Full Moon, no casual observer has a really accurate idea of how big the Moon looks in the sky as there is usually nothing to compare it against. Add to this the well-known "Moon illusion", where the Moon looks larger when close to the horizon than when high in the sky, and a variation in apparent diameter of 8% will easily go un-noticed. The increase in brightness will be even more difficult to detect, as the sensitivity of the eye varies enormously depending on the intensity of the light: this is to improve our ability to see in low light while protecting it from extremes. An actual increase in intensity of 100-fold will thus in fact only appear around twice as bright. An increase of even 21% will therefore be very difficult to detect in isolation. As with all aspects of the Supermoon phenomenon, the "detectability" of changes in size and brightness is quite a complex issue and so I shall be considering it later in this article.
A further, psychological, factor is that, because the Moon is always so very much brighter when it is full than when at partial phase, it is easy for an observer who only rarely looks at the sky, but has been attracted to do so because of the hype, to imagine that the tremendous brilliance of a particular Full Moon is due to it being a Supermoon, rather than just being "normal". The much-increased brightness at full phase is a real phenomenon however, not an illusion. It is caused by the strange properties of the Moon's surface, which cause it to reflect much less light than one might imagine if it is illuminated at an angle. Unfortunately, this phenomenon (often called the "opposition effect") further confuses the Supermoon issue because, as the Moon's orbit is inclined with respect to the orbit of the Earth, the Moon is almost always seen at a slight angle even at Full Moon. The calculations are surprisingly involved though so, once more, a full discussion will have to wait until later. However, it is clear that Supermoons may not actually be as "Super" as they have been made out to be.
Having, to some extent, debunked the idea that Supermoons are particularly dramatic, I need to briefly consider the other part of the media reports - that they happen every 13 months. This is, unfortunately, quite a difficult topic to discuss as it depends on a more detailed appreciation of the characteristics of the Moon's orbit than described above. I shall therefore, for the moment, just have to state without justification that the time between Full Moons is 1.98 days greater than the time it takes for the Moon to go from one perigee to the next. Therefore, if a particular Full Moon is a Supermoon (because it happens very close to the time when the Moon is at perigee), the next Full Moon will not be "Super" because Full Moon and perigee will no longer align. There will not be another Supermoon until they align again: this will happen when the mis-match has accumulated sufficiently to become equal to an entire perigee-to-perigee period (27.55 days). This will take about 14 Full Moon periods, or just over 413 days. Now 413 days is 13 months 18 days, which accounts for the "once every 13 months" statement. However, the re-alignment will not be quite exact (as 14 times 1.98 is actually 27.72 days rather than exactly 27.55) and so, although this line-up will probably be close enough for another Supermoon to occur, the one after that will generally not be close enough and so will not be a Supermoon. So, although the minimum time between Supermoons is indeed just over 13 months, it is not true to say that a Supermoon will happen every 13 months. The media reports thus have some truth in them, but not the whole truth.
Where do we go from here then? Into greater complexity, I'm afraid! I mentioned several times above that I would explore matters more fully "later in this article". That time is now, but I do recognize that not everyone will want to delve more deeply. Those that are satisfied (or bemused!) by the discussion so far should thus click here. This will take them close to the end of the article, where there is a section illustrating the difficulty of perceiving the size and brightness differences of a Supermoon before a Summary wraps things up.
For those of you brave (or foolish!) enough to plough on, I would say that now I have touched upon some of the difficulties involved in "Supermoon theory" and told you what a Supermoon is not, it must be time to find out what it is.
The first question to consider is the rather complex issue of how one actually defines a Supermoon. The original definition, coined as recently as 1979 by the astrologer Richard Nolle, was "a Full Moon occurring with the Moon within 90% of its closest approach to the Earth on that orbit". This definition thus uses a criterion based on distance, which has the great advantage that the apparent size of the Moon, which is one of the key characteristics of a Supermoon, depends solely on its distance. Although it is, as we have seen, not all that easy for a casual observer to notice the change in size, it will show up clearly if one takes a picture of the Moon and so defining a Supermoon in terms of distance is still a useful way of looking at things.
Unfortunately, this definition simply doesn't make sense as originally stated! The "closest approach" is the smallest Earth-Moon distance on a given orbit and so, by definition, at no other instant will the distance be less than this value, let alone as little as 90% of it! What is really meant, I assume, is "within no more than an additional 10% of its closest approach distance" i.e. a factor of 110% rather than 90%. This semantic clanger notwithstanding, the overwhelming problem with this definition is that, because the absolute largest Earth-Moon distance is only 14% greater than the absolute smallest distance, it's quite difficult to find a Full Moon which is not a Supermoon under this rule! For example, running forward from the Supermoon of August 2014 we find that, despite the fact that it is only 4 days from the next apogee and so is no less than 397241km from the Earth, the Full Moon on 5th January 2015 is still within the [semantically correct!] limit of 110% of the nearest perigee (108.9%, in fact) and so would qualify as a Supermoon!! Possibly for this reason, the definition has subtly shifted to use the absolute smallest perigee rather than the perigee on a given orbit. On this basis 5th January is not a Supermoon (the ratio is now 111.5%). However, those in September, October, November and December 2014 still would be and so this revised definition doesn't really solve the problem. A new limit of, it is claimed, 99% of the absolute minimum has therefore been proposed [it should actually be 101% of course!] but experiments I carried out with the Solex astronomical calculation program show that this should surely be 99.9% [i.e. actually 100.1%] else still far too many Full Moons are deemed "Super". However this criterion, which works out to be "closer than 356709km", eliminates the much-hyped 10th August 2014 event! (at 356891km).
Apart from the problem of deciding exactly where to draw the line, the great disadvantage of a distance-based criterion is its inability to predict close approaches with any certainty. As mentioned at the beginning of this article, the Moon's orbit is quite variable and the variations themselves have variation. The Earth-Moon distance is therefore subject to fluctuations at many different periodicities and so it is unclear whether patterns that repeat at regular intervals will exist or not. So, while one can easily say when the closest approach on a given orbit will occur, it is difficult to predict what the actual Earth-Moon distance will be at that point and thus whether a Full Moon occurring around then will be "Super" or not. This means it is not possible to determine when the next distance-based Supermoon will be without recourse to an astronomical calculation program such as Solex.
All is not entirely lost though, as it turns out that certain patterns do exist but are only noticeable "retrospectively" i.e. once one has found the nearest Full Moons by calculation it is then clear that their dates fall into recognisable sequences. The periodicities involved in these sequences are more relevant to other definitions of a Supermoon though, so I shall deal with these first before coming back to the distance-based definition.
An alternative way of defining a Supermoon which avoids the major problem with the purely distance-based definition is the "astronomical" one: a Full Moon is "Super" only if it occurs near in time to its closest approach to Earth on that orbit, rather than near in distance. This is called a "perigean" Full Moon. The great advantage of this method is that if we define "near" tightly enough (a criterion of plus or minus 1 hour works well) it turns out there will automatically be only (at most) one Supermoon per year - very useful. Even better, because of the way the Sun affects the Moon's orbit, the Full Moon nearest in time to perigee in any year will also be that with the least Earth-Moon distance that year. The time-based definition thus reduces the number of Supermoons while preserving the concept of much decreased distance. As we shall see, the definition also gives us a way of accurately predicting the interval between successive Supermoons, which the distance criterion does not - also very useful.
One could of course argue that the +/-1hr condition is as arbitrary as any distance-based definition, but I would disagree. Choosing an appropriate time-limit helps us enormously, as it actually simplifies the problem, whereas choosing a distance-limit merely reduces the number of Full Moons regarded as "Super" without giving us any additional predictive powers.
Before embarking on any calculations, I had better firstly explain why every Full Moon is not a Supermoon under this definition i.e. why Full Moon and perigee do not always coincide. This is because the time it takes to go from Full Moon to Full Moon is significantly longer than the time taken to go from perigee to perigee. In fact, while the Full Moon interval is the well-known 29.53 days of a lunar month, the perigee interval is only 27.55 days. Why? Because whereas the perigee interval is purely a characteristic of the Moon's orbit, the Full Moon interval involves an observer on the Earth, which is itself in orbit - round the Sun. Therefore in the time it takes the Moon to complete a full circuit of its orbit the Earth has also moved round its orbit somewhat, meaning that to re-establish the position where Sun, Earth and Moon are in a line (i.e. Full Moon), the Moon has to keep going for a while longer. By the time the Moon is full, therefore, it will be well past perigee.
The situation is illustrated by the diagrams below. The yellow disc represents the Sun, the cyan disc the Earth (on its slightly eccentric orbit) and the green one the Moon (on its considerably eccentric orbit): the viewpoint is assumed to be from above the Earth's northern hemisphere and so the orbital direction of both Earth and Moon is anti-clockwise. I hope it goes without saying that nothing is to scale!! The first diagram shows Full Moon at perigee, and the second shows the next Full Moon afterwards. It is clear that to re-establish the Full Moon position the Moon has had to travel past perigee and so the two instants no longer coincide.
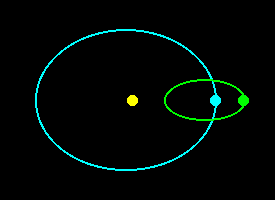
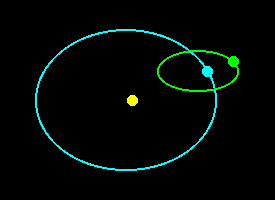
There will not be a further Supermoon until the Full Moon position has moved round the orbit sufficiently for it to arrive back at perigee. The key to determining how long this will take is to realise that in the time between successive perigean Supermoons the Moon must have completed a whole number of both Full Moon (synodic) and perigee (anomalistic) cycles. Calculations show that the first interval which is closely equal to a whole number of both the synodic and anomalistic periods is 413.37 days (14 x synodic = 413.43, 15 x anomalistic = 413.32). In other words, the shortest possible interval between perigean Full Moons is 413.37 days: this is the reason why there will be at most one Supermoon in a year. However, this does not mean there will necessarily be a Supermoon every 413.37 days, because the multiples are not exactly equal. The difference of 2hrs 38mins is much greater than our criterion of less than 1hr and so it would seem not to be possible to have even two successive Supermoons at this interval. However, variability in the orbital periods due to perturbations by the Sun can sometimes cause the difference to reduce, permitting a short series of Supermoons. A much closer match is found with 251 synodic periods and 269 anomalistic periods - the difference of just 5mins 36sec will permit there to be many successive Supermoons at this interval, the duration of which is 7412.18 days, or 20 years 3 months 16 days.
But are these calculations supported by the facts? To find out, I firstly calculated the interval between the four Supermoons which happened in the years just prior to me writing this article - in fact each year from 2011 to 2014. In whole days, the intervals were 414, 413 & 413, confirming my statement above that this is a Supermoon period and that a short sequence of them might be possible. I then used the Lunar Perigee and Apogee Calculator at www.fourmilab.ch to search for each Supermoon (by the "time" criterion) from the present day forwards and again calculated the time interval between them. I found that the next one after 10th August 2014 will be 25th November 2034: an interval of 7412 days! So far, so good. Things got a little more "interesting" after this though, which led me down some rather convoluted routes which many might consider a diversion. I have thus put these wanderings down the by-roads of the problem on another page, which those who like to take the long way round can investigate by clicking here. However, these extra investigations did not alter the fact that the fundamental periodicities of "time-based" (perigean) Supermoons are 413.37 and 7412.18 days.
So, by adopting a time-based definition we have been able to limit the number of Supermoons and have also been able to say a very great deal about their periodicity - problem solved, therefore? Unfortunately, no. Given that the characteristic of a Supermoon which is most often mentioned is its brightness, is it not best to emphasise this by only counting Full Moons which are exceptionally bright, irrespective of the exact details of the orbital configuration? This does complicate matters considerably though because a brightness criterion takes in not only the the Sun-Moon and Moon-Earth distances but also the "bright Full Moons" effect alluded to much earlier. Time to discuss this in more detail, therefore.
The "bright Full Moons" effect is in fact a general phenomenon, observed in the case of asteroids as well as the Moon, which even has a name: either the prosaic "opposition effect" or the eponymous "Seeliger effect" after Hugo von Seeliger, the astronomer who did pioneering work on the subject. He found that the amount of sunlight a body will reflect depends very strongly on the scattering properties of its surface material. Airless solar system bodies tend to have surfaces with a very fine-grained "micro-structure" due to their bombardment over aeons by solar particles and general solar system debris. The consequence is that, although much of the incident sunlight is scattered omni-directionally and so can always be seen by an observer, the micro-structure results in a large proportion being reflected back directly towards the Sun i.e. usually away from the observer, reducing the overall apparent brightness of the body from what it would be if it were uniformly reflective. It's only when, from the point of view of the observer, the body is opposite the Sun in the sky that the directly-reflected sunlight heads towards the observer and so can be seen by them, adding considerably to the body's brightness. This "double whammy", of a reduction in brightness at part-phase due to light being reflected away from the observer coupled with an enhancement in brightness at full phase because the formerly "reflected away" light is now directed towards the observer, is what makes a Full Moon so much brighter than one at part phase. Indeed, a Full Moon is fully 121/2 times as bright as a First, or Last, Quarter Moon (which has half the Moon's visible surface illuminated), rather than the factor of 2 one would expect for a uniformly-reflective body: a dramatic difference.
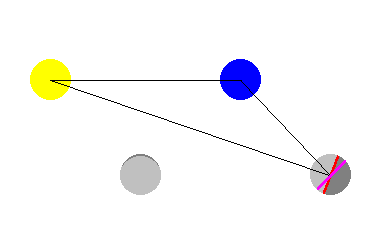
To understand why the Seeliger effect influences the brightness of each individual Full Moon it is necessary to realise that the Moon has a phase in the "vertical" as well as the "horizontal" direction. Its "horizontal" phase (the change from New to First Quarter to Full to Last Quarter to New again) is caused by its motion around its orbit. Its "vertical" phase is due to the fact that the plane of its orbit is tilted with respect to that of the Earth and so even at Full Moon there is rarely an exact straight line from the Sun through the centre of the Earth to the Moon. This is possible about every six months though, as the plane of the Moon's orbit rotates only slowly with respect to the motion of the Earth round the Sun and so will cut the Sun-Earth line about twice a year. However, when this does happen the result is a lunar eclipse, and they are not known for being excessively bright! All non-eclipsed Full Moons will thus be slightly above or below the Sun-Earth line and so an observer on the Earth will see their south or north poles (respectively) marginally in shadow i.e. they will have a "vertical phase". Because of the highly non-linear way the opposition effect depends on the phase angle, when the Moon is at its greatest offset (of only 5deg 18min, resulting in a illuminated fraction of 99.79%), the observed brightness is decreased by a massive 15%. Even a best-case perihelion Supermoon can thus be dimmed back to only a little above average brightness if it occurs when the orbit has an unfavourable orientation.
 | The "vertical phase" effect can be appreciated by reference to this diagram (also used in another of my articles). The yellow disc represents the Sun, the blue the Earth and the grey the Moon, with the whole ensemble viewed "from the side" i.e. in the plane of the Earth's orbit round the Sun. I hope I don't need to say that the diagram is not to scale!! Because the Moon is [almost] always either above or below the plane of the Earth's orbit, the part which is visible from the Earth will not be quite the same as the part which is illuminated by the Sun. In this diagram the visible part is delineated by the purple line and the illuminated part by the red line. There is clearly a small sliver which is visible but not illuminated, as shown on the inset view of the Moon as seen from the Earth: this is the "vertical phase". |
It therefore does not necessarily follow that the brightest Full Moons will be those nearest to perigee. In fact, there is good reason to think exactly the opposite as lunar orbital theory tells us that the very smallest perigees happen when the Moon is close to its maximum ecliptic latitude - this is the formal astronomical name for "distance above or below the Earth-Sun line". This configuration will cause a severe reduction in brightness due to the opposition effect, often more than compensating for the increased brightness due to the reduced distance. To determine the brightest Full Moons we thus need to carry out more detailed studies than just looking for Full Moons close to perigee (in either distance or time).
Calculations which attempted to list the very brightest Full Moons have been carried out by Jean Meeus, as detailed in Chapter 7 of his book "More Mathematical Astronomy Morsels" (Willmann-Bell Inc, 2002), with the result that the fifteen brightest Full Moons he found in the period 1800 to 2200 were distributed rather randomly in time: the interval between consecutive events varied from 8 to 113 years! Rather strangely though, he did not entirely eliminate from consideration those Full Moons which were also small-magnitude lunar eclipses. The result was that, unsurprisingly, most of the (alleged) brightest were actually very slightly in penumbral eclipse! I say "unsurprisingly" because of course when the Moon is in eclipse it is (by definition) also near to the Earth-Sun line and so the opposition effect will be very much reduced, resulting in a larger brightness value. However, being in eclipse (however slightly) will clearly affect the Moon's overall brightness and so to claim that a partially-eclipsed Moon is "among the brightest" does seem odd - it will indeed be brighter "per unit area" but almost certainly not in total, which is really what we are considering. It was therefore necessary for me to repeat these calculations with all eclipsed Moons excluded to get a better idea of the true state of affairs.
I did so by using Solex to generate a list of all the Full Moons in the 21st Century, together with their ecliptic latitude. The list was rather a long one (containing 1237 Full Moons, in fact!) and so I felt I had to cut down the field somewhat. Based on the earlier analysis of the factors that influence brightness, I eliminated all those with latitudes greater than 3 degrees (as these would have a large opposition effect) or less than 1 degree (as these would definitely be in eclipse), and also those with dates in April to September inclusive (as this is when the Earth is more distant from the Sun). It would have been much better to have eliminated all those with large Moon-Earth distances (as this has a greater effect on brightness than Sun-Moon distance) but the output produced by Solex does not give this parameter to enough significant figures. I then checked each remaining Full Moon against the NASA database of lunar eclipses so I could eliminate all those in eclipse, however slightly. Finally, I used Solex again to tell me the Sun-Moon and Moon-Earth distances of each of the 150 Full Moons remaining - a rather lengthy business despite the somewhat more tractable number. Now all I needed to do was work out the opposition effect for each of them and I would have a final brightness figure. This was easier said than done, however!
Although Meeus fully explored the opposition effect in his Chapter on "Brightest Full Moons" he did not give a formula for calculating the magnitude of the effect from the latitude. I thus needed to determine two things - the relationship between latitude and illuminated fraction and that between illuminated fraction and opposition effect magnitude. The first was relatively easy to do, as there is a standard formula relating phase angle to illuminated fraction and one may assume that the Moon's ["vertical"] phase angle is equal to its latitude, given the very small angle between the Earth-Sun and Sun-Moon lines due to the great distance of the Sun from the Earth/Moon system. The second was much harder though, as I could only work from the scant information given by Meeus rather than a numerical expression. I had just three statements and two facts to go on. Firstly, the brightness at maximum latitude (5deg 18mins) was said to decrease to 85%; at phase angles of +10deg and -10deg it was said to average 77.4%, and Full Moon was said to be 121/2 times as bright as half-phase. Then, Meeus had calculated the brightness both with and without the phase effect for just one Full Moon, so the ratio of these two values gave me one "fixed point", where the reduction for a given lunar latitude was known with certainty. Finally, it is self-evident that, were it not for the fact that this situation represents a central total lunar eclipse (!), at a phase angle of zero there would be no reduction i.e. the factor would be 100%. Using the standard formula to convert from latitude/phase angle to illuminated fraction, I plotted these values on a graph and used the Excel curve-fitting facility to derive an equation for the relation between them. I found that the various numbers were not quite mutually consistent, so a slight adjustment was needed to get a good overall result, but eventually I was in a position to begin calculating!
I firstly worked out a "before phase effect" brightness value for all the remaining Full Moons. Many results clustered round the value 1.00 - the brightness at average Sun-Moon and Moon-Earth distances - which is what you would expect for an essentially random collection of Full Moons. However there were thirty-eight which had values greater than 1.15, averaging 1.18 in fact (note that this is not because brightness values a little lower than this cannot occur - as previously mentioned - but because I had pre-selected the data: the values near to unity were for the Full Moons with large Moon-Earth distances which I had been unable to eliminate). I applied the full brightness calculation to the subset with high initial values and then normalised the results to show how much brighter the Supermoon would be relative to a "normal" Full Moon i.e. one at average distance from the Sun, average distance from the Earth and average latitude: I took this to be 3deg 25min (the mean value between the eclipse limit and the absolute maximum). Finally, I selected only those which ended up at least 22% brighter than average - there were seventeen of these.
Of these Full Moons, which might reasonably be called Supermoons, the absolute brightest was on 30th January 2010 and the brightest from now until the end of the century will be on 22nd January 2027. The others were/are on 11th January 2009, 2nd January 2018, 17th October 2024, 10th February 2028, 13th January 2036, 28th October 2042, 1st February 2045, 20th February 2046, 23rd January 2054, 13th February 2063, 3rd March 2064, 23rd February 2081, 14th March 2082, 11th November 2095 and 6th March 2099. The most surprising finding was that these Supermoons are up to 26% brighter than average! But how can this be, given that the basic "distance-based" calculations indicated that an optimum Supermoon could be just 21% brighter? The reason is of course the opposition effect, coupled with the finding mentioned earlier that the smallest Moon-Earth distances are associated with the largest latitudes: the brightness reduction due to the latter more than makes up for the increase due to the former. This is not to say that the distances associated with the brightest Full Moons are exactly large (the average is 357129km, compared to the absolute minimum of 356353km) but the latitude is the killer factor: the decrease in latitude from the 3deg 25min of an "average" Full Moon to a value of around 1deg 54min typical of Supermoons simply trumps the distance factor, resulting in a brighter Full Moon overall.
As with the increase in size, the increase in brightness of a Supermoon means little unless an observer can actually detect it. The first problem is one of definition - what do we mean by, for example, "twice as bright"? Unlike weight, there is no commonly-used measure of brightness and so we have no natural "feel" for how bright things are in an absolute sense. One can of course measure brightness very accurately using scientific equipment but here we run into the second problem - the non-linear response of the eye. Because it has to deal with an enormous natural range of brightness, from starlight in the desert to full sun to lightning flashes, the eye becomes "super-sensitized" at low light levels and desensitized at high levels. This means that although measuring equipment may tell us that one object is emitting twice as much "light power" as another, it is found experimentally that the degree to which the one looks brighter than the other will depend on how bright they are in an absolute sense. To put it another way, the minimum change in brightness which is "just discernible" increases with the actual brightness level i.e. the brighter an object is the greater the change in its brightness needs to be before the difference will be noticed by an observer.
The characteristic response of the eye is taken into account by the Stellar Magnitude system of measuring the apparent brightness of heavenly bodies. In this scheme 5 magnitudes corresponds to a brightness difference of 100-fold and so 1 magnitude represents a difference of 2.512 times (the 5th root of 100, in fact). In general, if R is the brightness ratio the magnitude difference is equal to log(R)/log(2.512) which, because log(2.512) equals 0.4, can be simplified to M = 2.5 x log(R). Taking our Supermoon brightness ratio of 1.26, the magnitude difference comes out as just 0.25. But how can this help us with our "minimum discernible difference" problem? Well, a trained observer of variable stars can, under ideal viewing conditions, detect that a star is 0.1 magnitudes brighter than one close by when both of them are around magnitude 6. Because the minimum discernible difference in brightness increases with the actual brightness level, the Moon, being very much brighter than a star, will need to change its brightness very much more than a star before this change will be perceptible. The Moon is about 18.6 magnitudes brighter than a 6th magnitude star and so, taking 0.1 magnitudes at mag. 6 as our starting point, its brightness would need to change by 0.1 x 18.6 / 6 = 0.31 magnitudes (or a factor of 1.33 times) to be just noticeable. This, you will note, is a significantly greater amount than the brightness increase of a Supermoon relative to an average Full Moon (1.26), meaning that a Supermoon could not be distinguished from an average Full Moon. However, the brightness difference between a Supermoon and a "worst case" Full Moon - apogee plus aphelion plus unfavourable inclination - which is a factor of about 1.42, or 0.38 magnitudes, is greater than the amount required for the change to be "just noticeable". In principle, therefore, the extra brightness of a Supermoon relative to a "Mini Moon" could be distinguished, but it wouldn't be particularly obvious. One must always remember though that the "trained variable star observer" situation requires both objects to be visible at the same time, so a direct comparison can be made. This is, clearly, never the case with Full Moons and so an accurate estimate of brightness will be even more difficult for a non-expert to make. And that's before we consider the time interval between successive Full Moons (as in the case of their size) and such things as the height of the Moon above the horizon - the lower the Moon is, the more its light will be absorbed by the atmosphere - and interfering effects such as air pollution, haze, thin cloud etc., which may not be obvious to the observer. All-in-all, therefore, for all practical purposes it is not possible to discern the difference in brightness of any Full Moon, let alone notice that Supermoons are "brighter than average".
A highly significant finding was that there are many sequences of Supermoon dates separated by just over 18 calendar years - for example (2009-2027-2045-2063-2081-2099); (2010-2028-2046-2064-2082), and (2018-2036-2054). This interval - more precisely 6585.3 days or 18 years 11 days 8 hours - is the Saros Period, which is very important when considering solar and lunar eclipses as it gives the interval between eclipses of a very similar "character": in particular the Moon's distance from the Earth and the track of the eclipse over the Earth's surface. This is because the Moon's orbital parameters repeat very closely at this interval. Importantly, this is true for any pair of orbits separated by a Saros Period, not just those involving eclipses.
The reason why Supermoons re-occur at Saros Period intervals should now be clear. We know that for a Full Moon to be "Super" it must be close to both the Earth and the Sun and, critically, at a relatively small latitude. Once these conditions have been set up they will repeat fairly exactly at intervals of a Saros Period - I say "fairly" because, as the Saros Period is 11 days longer than a whole number of years, the calendar date of the Full Moon, and hence the Earth's distance from the Sun, will vary slightly and the accuracy of the repetition of the other orbital parameters is not quite exact anyway. This will mean that a sequence of Supermoons at the Saros Period interval will only run until the Full Moon date slips out of the period when the Earth is near the Sun (October to March); or the Moon-Earth distance becomes excessive, or the latitude either becomes great enough for the opposition effect to reduce the brightness or small enough for the Full Moon to become a lunar eclipse. Supermoon sequences will thus continuously be "born", run their course, and then "die". For example, the candidate Supermoon in 2006 (18yrs before 2024) just fails to make the grade, at 21.4%, as its date (7th October) is close to the limit, and the perigean Full Moon in 2060 (18yrs after 2042) is ruled out because it is actually in eclipse - if only just! - and so does not count. Sequences can be quite long though, if their starting date is advantageous and the orbital repetitions unique to a particular sequence are accurate enough. For example, the sequence starting in 2010 listed above continues forward from 2082 to 2100 but stops there because its date in 2118 (6th April) is late enough to cause its brightness to fall just below the threshold (21.1%): the Full Moons after that are also just in eclipse. The sequence can be tracked as far back as 23rd October 1847, when a combination of greater distance from both Sun and Earth again reduce its brightness fractionally below the threshold (21.9%). This timespan - 270 years 165 days - equals 15 Saros Periods and is just about the maximum possible.
Having found these Saros Period sequences, one can then see that the "offset" between them tends to be strongly related to the 413-day period. For example, the members of the sequence starting with the "near miss" in 2006 are all 2 x 413 days before those in the sequence starting in 2009, which are themselves all 384 days before those in the sequence starting in 2010. If one takes into account other near-miss sequences one can also find intervals of 3 x 384 and 2 x 399 days. One might have imagined that all the sequences would be some multiple of 413 days apart but, because "bright" Supermoons need a favourable combination of Sun-Moon distance, Moon-Earth distance and ecliptic latitude, a better trade-off between these factors can sometimes be achieved by slipping the interval by one lunation. Observe that (in whole numbers) 384 equals 413 minus 29, the length of a lunation, and 2 x 399 equals (2 x 413) minus 29 i.e. the 384-day offset represents a slip by one whole lunation and the 2 x 399-day offset represents a slip by one lunation over two 413-day cycles.
Now we have considered the various numbers which determine the periodicity of Supermoons, we can re-visit the situation as it relates to those determined on distance. As is the case for "bright" Supermoons, and for the same reason, there are many sequences of dates 18yrs apart. For example, there are very close Full Moons in 2016, 2034, 2052, 2070 & 2088 and also in 2018, 2036, 2054, 2072 & 2090. Corresponding members of these series are each 413 days apart, again as for bright Supermoons: note that there will not be any "non-413"-day intervals in this case as no trade-off between factors is involved.
There are, however, several Supermoons which are not in a sequence. This is due to the afore-mentioned unpredictability of the Earth-Moon distance, which results in the Full Moons which would have been part of the sequence being too distant to qualify as "Super". However, the interval between these "singleton" Supermoons and the immediately-preceding "sequence" Supermoon is still always a multiple of 413 days - moving forward from the present I found multiples of 5, 15, 14, 8 and then 5 again. This demonstrates the dependence of distance-based Supermoons on the perigee/Full Moon alignment interval and also the difficulty of predicting what the perigee distance might be for any given Full Moon.
Having considered in some detail the distance, brightness and periodicity of the various types of Supermoon, it is finally time to address the key question mentioned early in this article - can you tell the difference between a Supermoon and any other Full Moon anyway?
Taking the difference in size first, caused by the difference in distance, it is clear that this would certainly be very noticeable if one could see a Supermoon and an average Full Moon simultaneously. However, the task is much more difficult when the two are seen in isolation due to the lack of a reference against which to judge. This is even more so because rather than quickly jumping from "small" to "large" (which would make the difference quite obvious) the size of successive Full Moons varies smoothly from "small" (when Full Moon is near lunar apogee) through "average" to "large" (when Full Moon is near lunar perigee) and back again over a considerable number of lunations: 14, in fact. Thus even if a particular Full Moon is deemed "Super" it will not be significantly bigger than the one in the previous or next month, making it hard to recognise as being anything special. Furthermore, the size against which it is being judged as "Super" will have happened 7 or 14 months ago (in the cases of relative to "average" and to "smallest"), making it almost impossible to remember what the Full Moon looked like at that time.
It might be difficult to believe that a size difference of 14% would go almost un-noticed, so I have created some animations to make the point more strongly. These employ a white disc to represent the Full Moon, within a black square which is considerably larger than the disc to reduce the ease of comparing the size of the disc to the spacing between it and the edge of the square (in the same way that there is no size reference when observing the real Full Moon). Click or tap on each animation to start it, then again to stop it.
 | The first animation (to the left) consists of 14 "Full Moons", the number required for Full Moon to go from being aligned with perigee to alignment with apogee and back to perigee again, each of which is separated by a grey background to remove the possibility of directly comparing sizes. The disc starts as an average Full Moon and increases in size by 2% per frame until it reaches +8% (i.e. a Supermoon). It then decreases in size, also by 2% at each step, passing "average" and continuing on to -6%, to simulate an apogee Full Moon. Finally, it increases in size again up to "average". This cycle then repeats indefinitely. |
 |  |
| The second animation is exactly the same as the first one, except for the fact that there are no separator frames. | Finally, the third animation uses just the smallest and largest Full Moons, again with no separator. |
I hope you were surprised by what you saw! If I am right, you will have found it was noticeable that the size of the disc in the first animation was changing but that it was quite hard to follow the full cycle and thus to say which was the Supermoon. Also, you could probably not be certain how much larger the biggest disc was relative to the smallest. The continuous change in size should have been quite obvious in the second animation, but again it was probably difficult to be sure how much larger the biggest disc was. Finally, the last animation gave you the answer - I would guess it's a greater difference than you would have thought. Now consider that, if you found it tricky to remember the size of the disc over a few seconds, how much more difficult this would be if the Full Moons in question were separated by their actual interval of 29.53 days!
When we move on to the brightness of a Supermoon the situation is, if anything, even worse than for size. As already mentioned, the sensitivity of the eye varies depending on the ambient light level and so for a comparatively bright object such as the Moon the increase in brightness required for the difference to be "just noticeable" is actually quite large.
 | To illustrate the difficulty, I have constructed another animation - on the left here. This alternates between two frames, which represent a Full Moon at maximum brightness and one at minimum as seen by the human eye. I've made the two images the same size, to avoid confusing the issue, though of course the less-bright Full Moon would actually be smaller as the Moon would be at apogee at this time. The animation is running continuously, but you may not realise it's an animation at all as the two frames are only very slightly different. I have found it is a little easier to see the difference on an old-style (VDU) display than on a laptop, and definitely more obvious on a laptop if you view it "on the slant" i.e. from the side or from above or below. Try it! Assuming you can convince yourself that there really are two different frames, think how difficult it would be to distinguish between them if each was seen in isolation, several months apart! Not just "difficult", I would suggest, but totally impossible. |
So, what have we learnt about Supermoons? Mainly that most of what is said about them in the popular media is completely wrong! About the only statement that is correct (if but partly so) is the one about Supermoons being much closer to the Earth: while they are indeed closer, at best it is by just 8% relative to an average Full Moon, which doesn't really class as "much closer" in my book. The oft-quoted figure of 14% (usually in relation to the increase in apparent size) is not relative to an average Full Moon, as is frequently implied, but to the smallest possible size the Moon can be i.e. when it is at maximum apogee.
When we get on to the enhanced brightness of a Supermoon, things get even more confused. Again the usually quoted figure (30% brighter) can be ignored as, like the distance, it is relative to the Moon at maximum apogee. More importantly, it overlooks the varying distance of the Earth/Moon system from the Sun, which affects the amount of sunlight incident upon the Moon, and it takes no account of the tricky factor related to the percentage of the Moon which is illuminated, which is never 100% due to the tilt of the Moon's orbit relative to that of the Earth. Calculations taking all these factors into account show that the brightest Full Moons can be up to 26% brighter than average.
However, whether a Supermoon is 14% larger & 30% brighter as the hype would have you believe or 8% larger & 26% brighter than average as indicated by the calculations, the fact is that, to the casual observer, it won't actually look any different from "normal" Full Moons, entirely contrary to the media reports. This is partly for "observational" reasons - mainly the difficulty of remembering how large or bright previous Full Moons were, in order to compare them to the Supermoon - and partly for physiological reasons connected with the response of the eye to changes in brightness.
Finally, one must never forget that Supermoons (however they are defined) are not something completely out of the ordinary but just examples of one extreme end of the spectrum of close and/or bright Full Moons. There will thus be many Full Moons which are "nearly Super", making the recognition of true Supermoons even more problematic.
Moving on to how often Supermoons occur, and thus to when the next one will be, my analyses have shown why the media have been quoting "once every 13 months". This is certainly the minimum possible interval between "perigean" Supermoons (the 413-day value I calculated from the Full Moon and perigee periods) but it would seem that most commentators have been fooled by the sequence of such Supermoons in 2011,12,13 & 14 into thinking that they occur every 413 days, which we now know is very far from the truth. Those who persevered with my full analysis will know that a more accurate, if rather less succinct, answer would be "once every 20yrs 3mths 16days in general, but with runs of up to three or four at intervals of 1yr 1mth 18days every 283yrs or so". In particular, there will only be one perigean Supermoon in the period up to 2050, on 25th November 2034 (20yrs 3mths after the one in August 2014). One could say it's sheer bad luck that interest in Supermoons peaked just when there was a sequence running, but it's disappointing that even such as the BBC took "once every 13 months" at face value and failed to do a little bit of research to validate it.
My full analysis also showed that it is not possible to give a simple repetition interval for Supermoons defined on distance or brightness criteria, due to the complex nature of the variations in the Moon's orbit, so I shall give lists instead. The tables below thus show the nearest and brightest Full Moons in the period up to 2050. Note that only two of the five nearest Full Moons are also among the brightest. This is because of a large opposition effect due to the unfavourable orientation of the lunar orbit at the time of the other three (a Sun-Earth-Moon angle averaging 4.87deg): this confirms the statement I made in the full analysis that the very smallest perigees tend to be associated with the least favourable orientations. Conversely, despite its considerably greater distance (357645km) the bright Full Moon in January 2027 is not just the brighest up to 2050, it is in fact the brightest Full Moon from now until the end of the 21st Century. This is because its highly favourable orientation (an offset of just 1.66deg) reduces the opposition effect so much.
|
|
Note that in order to reduce the number of Supermoons in each category to what I felt was a reasonable number I have had to apply a cut-off in each case. This was "no more than 0.1% greater than the absolute minimum perigee distance" for "near" Supermoons (which comes out as "no more distant than 356709km") and "at least 22% brighter than average" for bright Supermoons. As mentioned right at the start of the article, this is inevitable given the continuous range of both distance and brightness and so the relatively small number of entries in both lists is purely arbitrary, rather than being an indication that close or bright Supermoons are something completely out of the ordinary.
Don't believe everything you hear or read about so-called Supermoons! While it may be interesting to know that a certain Full Moon is nearer (and thus larger) or brighter than any other this decade or century, unless you are a particularly skilled and diligent observer or have a camera or photometer to hand you're most unlikely to notice anything out of the ordinary.
Pity to spoil a good story, but the facts don't lie!
I briefly mentioned right at the start of this article that the distances I was quoting were measured "centre-to-centre", rather than relative to an observer on the surface of the Earth, and of course when referring to an observation of a Supermoon I have implicitly assumed that the observer will be able to make their observation exactly at the instant of Full Moon. These two assumptions make the calculations easier, but I really must now examine them more closely. However, while the additional conclusions reached are interesting they are slightly peripheral to the main argument and so I have included them as an "extra page". To read it and, I trust, be even more convinced that Supermoons are hopelessly over-hyped, click here.
I would like to thank in particular Roger Firth, but also the members of the Auld Phartz hiking, drinking and social club, for the many helpful comments and suggestions received during the initial construction of this article, and Jill Allum for the discussions which led to the writing of the Postscript.