Supermoons - Postscript

The main reason I used centre-to-centre distance rather than observer-to-Moon is because the latter distance will depend on where the observer is located and when they carry out their observation, rather than just on the details of a particular Supermoon. This makes drawing any general conclusions rather difficult due to the large number of variables involved.

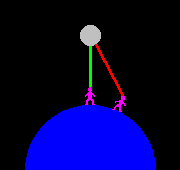The observer's location is so important because the Moon is at the least distance from an observer only when it is exactly at the zenith i.e directly overhead. The diagram (which is clearly not to scale!) illustrates this - the green line, from the observer to the Moon at the zenith, is not only shorter than the red line, from the observer to the Moon not at the zenith, but is in fact the shortest possible observer-to-Moon distance.

While the diagram is only in two dimensions, it should be obvious that an offset towards any point on the observer's horizon will increase the observer-to-Moon distance. This offset can occur for two reasons:- 1) the observer's latitude, coupled with the position of the Moon on its orbit (which is tilted with respect to the Earth's equator), may mean that it is simply not possible for the observer to see the Moon at the zenith, and 2) the Moon may be still on its way up to its highest point (i.e. it is still rising) or descending from it (i.e. it has begun to set). This latter point is equivalent to saying that the time is not local midnight, as the Full Moon is always at its highest point at this instant. To see this remember that, when Full, the Moon is directly opposite the Sun in the sky (i.e. the Sun, the Earth and the Moon are in a straight line at this moment) and that the Sun is at its highest point at local noon. If the Sun is at its highest at noon on one side of the Earth, it follows that the Full Moon must be at its highest at midnight on the other side. Importantly, it will then be due South (in the northern hemisphere), and this result is in fact more general than "at midnight", as it is true for the Moon at any phase - it will always be nearest to the observer when due South.

So, unless a Supermoon is observed at midnight from a location where Full Moon occurs exactly at that time and, at that instant, it can be seen exactly at the zenith, it will always be further away from the observer than a simple calculation would indicate, and will therefore be seen to be slightly smaller and thus slightly less bright.

The other assumption - that the Supermoon is observed exactly at Full Moon - overlaps somewhat with the previous one, but the issue I was mainly thinking of is when the timing of Full Moon simply makes it impossible to view it from a given location; for example, if Full Moon occurs during daylight at that location. When then is the best time to view in order to see the biggest possible "Full Moon" (which I put in italics because it will be either before or after the instant of true Full Moon). We know from the above analysis that this must be when it is due South, but should it be during the night before or the night after? The answer to this question depends on the time of perigee (both in absolute terms and whether Full Moon is before or after it); where you are on the Earth's surface; what time of year it is (because the Moon is generally higher in the sky in winter, due to the tilt of the Earth's axis), and where the Moon is on its orbit. This last factor comes into the reckoning because of the tilt of the Moon's orbit relative to the Earth's equator. When the Moon is traversing the "upwards tilted" part of its orbit it appears higher in the sky than when traversing the "downwards tilted" part. There are many possible combinations, so I will just give one situation as an example - the Supermoon of 14th November 2016 (which was when I added this Postscript).

In this case, perigee was at 11:22GMT on the 14th and Full Moon was at 13:52GMT. The night before was therefore closer to perigee than the night after, so the Earth-Moon distance should have been smaller then. And indeed it was. When due South, the Moon's distance was 356772km at 23:09GMT the night before as compared to 356797km at 00:09GMT the night after. This is the centre-to-centre distance however. When considering the observer-to-Moon distance the "closer when higher" factor discussed above comes into play. The night before, the Moon's altitude was 48.5deg but the night after it was 52.2deg: greater because it was nearer to the "high point" of its orbit. At my location, it turned out that the second factor more than compensated for the first, so the observer-to-Moon distance was less the night after Full Moon than the one before: 351733km as compared to 351964km. The best time to observe was therefore just after the midnight of 14th/15th November.

But how much closer could I have seen it if viewing from a position when the Moon was at the zenith on the better night? Well, if I had travelled directly south from my location to 15deg 13min North the Moon would have been directly overhead at the same 00:09GMT, when the distance would have been 350422km - a significant 1311km nearer. This distance is very much greater than the 263km that even the closest Supermoon in the table is below the limit I have taken for a Full Moon to be "super" (356709km centre-to-centre), and so the best way to get an impression of what a Supermoon would look like at your location is therefore simply to travel south at the time of a "somewhat closer than usual" Full Moon rather than wait at home for a "proper" one! This does emphasise the fact that your experience depends very much on where you are and when you view. The range over which the above parameters can vary has a considerable effect on the observer-to-Moon distance, and so your "super" could easily be someone else's "ordinary"! (and vice-versa, of course). To check this out, I looked for any case where a "non-super" Full Moon could be seen from my location at a distance closer than the Supermoon of 2016.

I didn't have to look far! The Full Moon at 13:20GMT on 5th November 2025 has an associated perigee at 22:30GMT on the same day. The perigee distance is 356832km, so the Full Moon is not "super" by my definition. However, with the Moon due South from my location (at 23:58GMT), its distance from me will be just 351336km - a considerable 397km less than the best distance achievable in 2016. We therefore have a "non-super" Full Moon which will actually look bigger than the second-closest Supermoon! This result comes about because, in this case, at the moment when the Moon is due South it is very close to perigee and it is also high in the sky (59.3deg): not only because of the "winter" date but also because it happens to be on the "high" part of its orbit. This further reinforces my argument that a casual observer will not be able to tell the difference between super and non-super Full Moons.

Having tackled the optimum cases, it's finally time to consider the worst. It should be obvious that things will get worse if you travel north so I'm not going to consider that option. I will instead show what happens if you do not observe when the Moon is due South but instead do so at moon-rise or moon-set i.e. with the Moon just on your horizon. The difference in distance in these cases is very great. This is not easy to see from the diagram, due to its lack of proper scale, but if you imagine the "Moon" to be much further distant you will realise that the observer will be able to see it almost up to the point where they are standing on the furthest left or right edge of the "Earth". The observer-to-Moon line will then be nearly a whole Earth-radius longer than the (extended) green line. In fact, for the 2016 Supermoon being considered, at the optimum viewing point the distance is 6241km, or 1.8%, greater than the due South distance when averaged between the moon-rise and moon-set distances. Even from my location there is an average increase of 4953km, or 1.4%, the distance at moon-rise being 356343km and at moon-set 357029km. These distances are so much greater than even the most generous "media" definition of a Supermoon that viewing at rise or set turns the Supermoon into very much an also-ran. It will be bigger than a "non-super" Full Moon seen on the horizon, to be sure, but cannot compare with even many ordinary Full Moons seen when due South.

There are a number of conclusions to be drawn from these analyses, the most important (and possibly most surprising) of which is that it is vital to observe Supermoons when they are due South (i.e. around midnight). Picking the correct location and the right night has some effect, but position in the sky is critical - it is 5 times as important as other factors. Supermoons seen near the horizon might be good from a scenic perspective, giving some foreground to any photographs, but they are then not "super" at all. It is thus rather ironic that the public are often advised that their best view of a Supermoon will be as it rises, whereas in fact it is about as bad as it can get. Another triumph for media-induced misconception!