As mentioned on the main page, the actual periodicities I found seemed to be nicely in agreement with my calculations. However, after the 7412 day interval from 10th August 2014 to 25th November 2034, the next ones were 6999 days, then 6999 again, then 7826. Do we have a problem? Well no - just a bit of "natural variation". In the same way that the variability in orbital periods can allow several Supermoons at intervals of 413 days, it can also cause the longer 7412 day period to either skip or add this interval - observe that 6999 = 7412 - 413 and 7826 = 7412 + 413 (well, not quite, but I have not shown the decimal part of the numbers). Continuing the search produced three more 6999s, two more 7412s, one 7825 and even an 8239 (which is equal to 7412 plus two lots of 413), before a single 413 and three more 6999s. I then found three 413s in a row before the 6999s and larger values started again.
The re-occurence of three 413s was interesting, duplicating the recent sequence with which I had started. The interval between these sequences was 284 years, so I looked ahead another 284 years to see whether a further sequence of 413-day Supermoons would appear - and yes, it did! However, the interval this time was actually 283 years, not 284. I therefore looked forward again, and this time found just a pair of 413-day intervals, 283 and 284 years after the middle one of the previous sequence of three. Yet another look forward gave me two series of three, at intervals of 284 and 283 years, and then a pair at 282 and 283 years. It seemed clear that although there was a pattern to all of this it was not entirely regular.
But what was producing this additional periodicity? The answer turned out to be a consequence of something I have not yet mentioned: the perigee-to-perigee period is not quite the same as the orbital period (as measured relative to the distant stars). This means that the perigee point drifts round the Moon's orbit - very quickly by astronomical standards. The result is that after one orbit of the Earth/Moon system round the Sun, the axis of the Moon's orbit (the line joining the perigee and apogee points) will be pointing in a considerably different direction from where it was at the start.
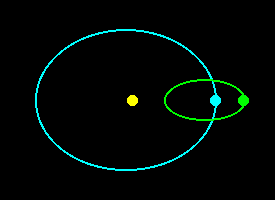
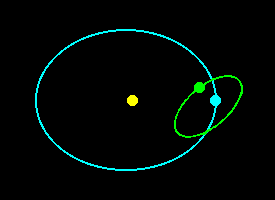
The situation is illustrated by the orbit diagrams below. As on the main page, yellow represents the Sun, cyan the Earth and green the Moon. The first diagram is the same as on the main page, showing Full Moon at perigee. The second shows the position one year later, when the apogee-perigee line has rotated considerably: note that the Moon is neither full nor at perigee, as there is not a complete number of Full Moon or perigee cycles in a year. We will not get another perigean Full Moon until the position shown in the third diagram has become established a little later. This, as stated on the main page, will be when the Moon has completed an integer number of both synodic and anomalistic orbits - 413.37 days.

And why is the perigee-to-perigee period longer than the orbital period? The reason is similar to the argument concerning the Full Moon interval. I have already mentioned that the Moon's perigee point drifts round its orbit: in fact, it takes 8.851 years to complete one circuit. The rotation is in the same sense as the Moon moves along its orbit (anti-clockwise when viewed from above the Earth's north pole), and so for the Moon to get back to its perigee point after having completed one orbit it must continue on for a little while longer - about 0.233 of a day, in fact. The anomalistic period is thus 27.55455 days while the orbital period (relative to the "distant stars") is 27.32168 days. However, this explanation leaves another issue pending - why does the axis of Moon's orbit rotate in the first place? This is due to the gravitational influence of the Sun, as are most disturbances to the orbits of the planets and their moons. Because the Moon's orbit has an appreciable eccentricity, the Sun's pull on the Moon as it traverses its orbital path is not equal at all points. In particular, at those times when the axis of the Moon's orbit is pointing towards the Sun, the pull on the Moon when it is the apogee of its orbit which is directed Sun-wards (placing the Moon at its nearest to the Sun) will be greater than when lunar perigee is so directed (as the Moon will then be further from the Sun). As I show in my article on Orbital Mechanics, a nett radial force applied at apogee will rotate the apogee-perigee line in the direction of orbital motion, which is what we find.
Now we know that the major axis of the Moon's orbit rotates in 8.851 years (3232.862 days), we can look at the third diagram above in another way. After 413.37 days the Earth-Sun line will have rotated by 360 x 413.37 / 365.2425 degrees, which is one full rotation plus 47.44deg. In the same time, the major axis will have rotated by 360 x 413.37 / 3232.862 degrees, which is 46.03deg. The result is that with the Full Moon at perigee once more the major axis will again [very nearly] align with the Earth-Sun line, as shown in the diagram. The re-alignment is not exact because the major axis in fact aligns with the Earth-Sun line every 411.76 days rather than the 413.37 day coincidence interval between Full Moons and perigee, but it is sufficiently close to give the chance of another Supermoon. Note that if we repeat the calculation for the more accurate 7412.18 day Full Moon/perigee period we get (ignoring full rotations) 105.79deg and 105.39deg respectively, confirming how much more accurate this period is.
The importance of the rotation of the major axis in this way is that the sequences of 413-day Supermoons are caused by variations in the synodic and anomalistic periods due to the influence of the Sun, which is at its greatest when a Full Moon occurs at the moment the axis of the Moon's orbit lies along the Earth-Sun line. However, as we have seen above, because of the rotation of the axis a perigean Full Moon will only rarely fall when it is aligned exactly with the Earth-Sun line - but how often, exactly? Well - we know that the major axis aligns with the Earth-Sun line every 411.76 days and that Full Moon and perigee coincide every 413.37 days. All three will thus occur together when integer multiples of the periods of 411.76 and 413.37 days come to the same number - exactly as per the initial calculation of the 413.37 day period itself.
Given the irregular periodicity I had already found I attacked the problem in reverse, by considering the 283-year interval. I found that it is very close to not only 250 times the Full Moon/perigee re-alignment period but also to 251 times the Earth-Sun line alignment period: the two are just 9 days different, which confirms my earlier statement: the interval of 283 years between groups of 413-day Supermoons is due to a resonance between the two alignment periods.
Just for interest, I carried on looking at 283-year intervals, expecting to find further sequences of 413-day Supermoons. What I actually found was rather more surprising. It turned out that although there were individual Supermoons every 283 years, there were no sequences for another 2258 years! There was then a pair of 413-day intervals but then none for a further 1127 years. Things then improved for a while, with only a few 283-year cycles not yielding 413-day Supermoons (but generally just the one) until a gap of 1400 years sudddenly appeared as we passed 10000AD. Going in the other direction, a similar thing happened. There were Supermoons in 1728, 1729, 1730 & 1731 (as there were in the years 2011 to 2014 inclusive) and then in 1444 & 1445, but the next pair was not until 260 & 259 BC - a gap of 1703 years. Further gaps of 1424 and 1142 years then appeared as I headed back in time, but I stopped at 3400BC as it seemed that the general behaviour had been confirmed.
While the gaps were rather unexpected, I was even more surprised to find that the nominally 283-year interval became steadily shorter as I moved to later dates, and lengthened as I went back in time. One might have expected a variation about the mean (as Full Moon/perigee cycles were added and dropped in order to keep the cycles in step), but not a consistent decrease. The change was quite significant - at the earliest dates I checked it was over 286 years and at the furthest into the future it was less than 279 years. The individual values were still multiples of the Full Moon/perigee interval of course, and so constituted a set of discrete values rather than a continuum, as can be seen by the chart below. Note, by the way, that all the "gaps" are multiples of the value of the nominally 283-year interval relevant at that epoch, reinforcing the finding that the period changes over time.
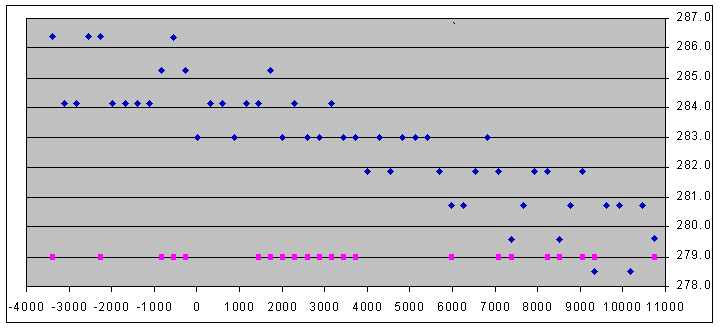
The blue markers show the successive values of the nominally 283-day interval, which clearly reduces as time goes on although the reduction is not regular. Click on the diagram to add a trendline (and again to remove it). The "fit factor" (the R2 value) does not improve if we move to a square-law or cubic fit, showing that although there is considerable scatter in the data the overall change in the interval is accurately linear. The actual values of the interval always correspond to multiples of the Full Moon/perigee and Earth-Sun line alignment periods which differ by 1 each time: the longest interval (286.4 years) is 253 times the Full Moon/perigee period and 254 times the Earth-Sun line alignment period, and the multipliers reduce by 1 each time until we get to the shortest interval (278.4 years) when they are 246 and 247 times respectively. The pink markers indicate the occurrence of multiple 413-day Supermoons: the "gaps" mentioned above are very obvious.
The reason for the gaps and the decrease in the period is not entirely clear. I can only assume that the gaps are due to the slight differences in the various periods accumulating sufficiently to cause the Full Moon and perigee interval to never quite fall into the +/-1hr criterion I am using: there are thus still "near miss" perigean Full Moons throughout the gaps, but not very accurately coincident ones. The most likely reason for the irregularity in the period is a mechanism similar to that which produced variations of 413 days on the basic 7412-day "more accurate" alignment interval mentioned at the top of this page: the dropping or adding of periods to keep the whole process in synchronisation. Support for this idea is given by the fact that the greatest deviations tend to occur when multiple 413-day Supermoons re-appear after gaps. There is also a "data analysis" issue, in that to determine an interval one has to choose the beginning and end points. I have assumed that, for example, the correct interval between two sets of three 413-day Supermoons is that between the middle event of each. This is not necessarily true though, as it will depend on the precise geometry of each occasion. Also, which do you choose from a run of two or four? However, changing the end point of one interval also changes the start point for the next and so if one interval goes up the next one must go down (and vice-versa). Therefore, while one can smooth out some of the irregularity by judicious choice of start and end points, the scope for doing this is limited and in any case the average overall picture (and the conclusions to be drawn from it) will be largely unchanged.
Unfortunately, I can find no good reason for the value of the nominally 283-year period to decrease in the consistent way it does. Certainly, there is no factor involved in the calculation of the Full Moon/perigee period or the rotation period of the Moon's major axis which changes fast enough over time, or by a sufficient amount, to suggest that the variation is due to a secular cause. The only parameter that does change by a large amount is the eccentricity of the Earth's orbit (which goes from 0.0186 in 3400BC to 0.0123 in 10,000AD) but while this may affect the likelihood of there being a sequence of Supermoons (as these are caused by extreme lunation and perigee-to-perigee intervals, which themselves are caused by the increased perturbational effect of the Sun, whose distance is affected by changes in the eccentricity), I can't see how it would affect the periodicities which combine to give the 283-year interval. To show definitively that the change in eccentricity might be the reason would require a very extended and detailed study though, which I feel would be outside the scope of even this extra page. I shall, therefore, end my consideration at this point - those with time on their hands are cordially invited to extend my analysis!
Finally, and while I really cannot believe it is significant, I must mention a strange numerical coincidence (for I assume that is all it is): 283 years is exactly equal to half the Tetradia period !! (more precisely, its value in 1932: 566 years). The Tetradia, as readers of my other articles will be aware, crops up in all sorts of situations involving eclipses and seems to determine such things as the frequency of four successive lunar eclipses. However, its magnitude varies much more rapidly with time than the change in the 283-year interval I discovered and so is unlikely to be the direct cause of that variation - hence my assumption that the numerical coincidence is just that. But you never know!