Latest update (March 2020) is right at the end of the article! Latest update (March 2020) is right at the end of the article!
Somewhat out of the blue, I received an email from an old school friend with whom I had kept in sporadic touch over the years, setting me an interesting problem. This is what he said:-
I'll pose the question as I have to countless others. Will you be the first to make a sensible response?
I am trying to answer an astronomical question that I first heard some 20 years ago and no one I asked could come up with a plausible answer. It has irked me ever since. When one looks at the Sun and the Moon in the sky together, why is it that the illuminated crescent of the Moon does NOT "point" at the Sun? More correctly the perpendicular bisector of the straight line joining the end points of the Moon's terminator does not point at the Sun. Intuitively one feels it should - as that is where the light is coming from. It is always around 20 - 30 degrees "off target".
While you ponder your response, I would add that I have posed the question widely, to university departments, astronomical institutions, colleagues of friends of ex-colleagues, and internet astronomy websites. Only about 50% have responded and no two responses (of about half a dozen I've had) even pursue vaguely similar thoughts. I find this rather odd, one would have expected a "standard response". Equally, no more than one can be correct!
Of the very few that seem worth considering (generally something to do with spherical & linear geometry), none seem to address the following conundrum: The observer, the Moon & the Sun, being 3 points, define a plane. Within any plane the laws of optics must apply (irrespective of any distances). Hence I cannot see why line-up does not occur.
Some responses, from apparently erudite institutions, seem eminently silly and whenever I attempt to challenge or query an argument the proponent ceases to correspond. I am beginning to develop a bit of a "conspiracy theory" complex about this!
With cautious optimism,
Roger.
Fortunately, I felt I knew the answer to this one so was able to give a pretty comprehensive reply. This sparked further debate, exploring many facets of the problem, which I felt might be of interest to other enquirers. I've thus written up the discussion in the form of a conversation, which forms the body of this article.
Before you read on, however, just in case you have no idea what Roger is talking about here's a panorama he sent me which he took on a trip to Carsington Reservoir, near Matlock in Derbyshire. The extreme field of view (150deg!) was achieved by combining four individual frames (taken using a "normal" lens, not wide-angle or fish-eye) using the Hugin "autostitch" program. The Moon can be seen just to the left of the clump of trees on the left, and of course the Sun is in the same position on the right (though its exact position is unclear due to the unavoidable over-exposure). Little can be seen in the full-size image, but if you click or tap on it to overlay an enlarged image of the Moon you can clearly see that the illuminated part is not pointing directly at the Sun. If it were, the line between the light and dark parts of the Moon (the terminator) would be approximately vertical: in fact, it is leaning over to the left to a noticeable extent i.e. the illuminated part is actually pointing above the position of the Sun. This is the conundrum Roger is describing.
Hi Roger,
Ah - that old chestnut! I would agree that some of the explanations given are decidedly dubious, and mostly show a failure to understand the situation. There is no simple geometric construction I can give you, unfortunately, so stand by for quite a long discussion, ranging over a number of issues.
The answer lies in the difficulty of comprehending a three-dimensional reality projected onto a two-dimensional curved surface - for that is what the image you see of the sky and its stars and planets actually is, because everything is effectively at infinity. The brain thus perceives everything in the night sky as being at the same distance from us, as if painted onto the inside of a dome covering our heads - the "sphere of the heavens" as the ancient writers put it. In a similar way, although intellect tells us we are standing on the surface of a globe our perception tells us we are at the centre of a flat disc, extending away for the same distance in every direction (cf Terry Pratchett!). The feeling that the sky is a dome and the Earth is a disc comes from the need to rotate our head and/or body to look in other directions: this rotation naturally generates an impression of curvature. The dome effect can be broken, however, most notably by clouds. As these are much closer to us it is easier to tell that some are further away than others. They thus appear to be hanging above us in their own individual positions, rather like multiple light-fittings attached to an invisible ceiling. Determining their exact height and distance is very difficult for an untrained observer however, due to the lack of a frame of reference. This gets worse at night, as contrast clues tend to vanish. Light cloud at night thus tends to be placed at infinity (particularly if it is not moving) and so appears to be part of the stellar background rather than hanging below it. The same effect can be noticed for aircraft. During the day they are seen as flying just above us but at night they are seen at infinity, as additional stars.
If the geometry of the sky we see above us were "flat" then the crescent would indeed always point directly at the Sun. However, it is not: it is, as previously stated, a domed-shaped two-dimensional surface. On such a surface, all actually-straight lines will appear to be curved. For example, other than at the (current) sub-solar point or at 90deg to it the Sun and Moon are seen to move across the sky not in a straight line but on a curve. This curve is the projection of the apparent path of Sun and Moon in three dimensions onto the dome-shaped visual field. The same must be true for the straight line between them: it will actually be seen as curved. The crescent Moon therefore does indeed point "directly" towards the Sun: it's just that you have to follow a curved line across the sky to move from one to the other rather than take the "straight line from A to B" approach.
If you sort of accept all the above, we need to consider why actually-straight lines are seen as curves. While a geometric derivation would clearly be possible (and this is something I might return to later), a "thought experiment" involving the sky-paths of Sun and Moon might be more convincing (especially to a non-mathematician). It is surely self-evident that they are curves, as anyone who has watched the Sun cross the sky from sunrise to sunset will easily confirm: the question is why that should be.
Consider firstly the case of a planet whose axis is bolt upright, with one Moon orbiting exactly in the equatorial plane. From the viewpoint of an observer at either pole, both the Sun and Moon are seen just on the horizon and their daily apparent motion due to the rotation of the planet is always parallel to the horizon i.e. a straight line in the x-direction. In this case, both the actual and apparent lines from Sun to Moon are straight, and so the crescent will at all times point directly towards the Sun (along the x-axis). Now, without changing anything else, move the observer to the equator. In this case the trajectory of both Sun and Moon is again a straight line, but this time the line goes from horizon to horizon via the zenith point (directly overhead) i.e. a straight line in the y-direction. Again, the crescent always points directly towards the Sun (along the y-axis) but this time the fact is only apparent if the observer lays on their back! It's the intermediate cases which cause the illusion, because there must be a smooth transition from a line parallel to the horizon to one running through the zenith as one moves from the pole to the equator. This requires the line of the trajectory to slowly tilt upwards which, because the ends of the line must remain fixed (as the sunrise and sunset points are always the same if there is no axial tilt), causes it to appear curved. The curvature increases until we get to the 45deg point, when it decreases to become zero again when the line crosses the zenith. The geometrical reason for the apparent curvature is that although the observed polar and equatorial trajectories are straight in the x- and y-directions respectively they are still curved in the z-direction (as they are actually circles). This z-direction curvature is not apparent in the limit cases but makes itself felt for intermediate cases.
I've constructed some diagrams to illustrate the above, showing both the geometry of the situation and also what the observer would actually see. In the upper part of the diagrams (the "geometrical" view) the light blue globe represents the Earth, the Moon is shown as light grey & maroon and the Sun is shown in yellow (the same apparent size as the Moon, as in real life). The dark grey disc is the plane of the Earth's equator, and so its outer edge represents the Celestial Equator. The all-encompassing purple circle represents "the sphere of the heavens" and the green circle represents the observer's visual horizon. I have shown the East and West points, as these are fixed. The precise direction of the North and South poles will depend on the orientation of the Earth, but in general terms the observer is shown looking towards the South.
In the lower part of the diagrams I have tried to show what the observer would see by turning to look due E, due S and due W (on the bottom row) and, while facing South, directly up at the zenith (at the top).The white line is the apparent path of the Sun and Moon across the sky. Note that, because the field of view of the human eye is relatively limited (about 50deg horizontally and rather less vertically), the views E, S and W would not cover the entire span of the horizon, nor would the observer be able to see the entire sky from horizon to zenith in just two "views". To emphasise this, I have shown the views with a gap between each of them. Click or tap on the diagram to move from one situation to the next.
 |
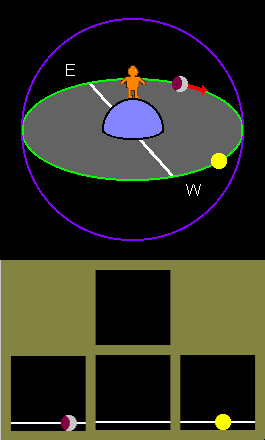In the first diagram the observer is at the North Pole and so his visual horizon lies exactly along the Celestial Equator. He thus sees the illuminated part of the Moon pointing directly at the Sun because they both move along the line of the horizon. The observer has moved to the equator in the second diagram, but as all diagrams are drawn from the perpective of the observer this has resulted in the Earth "lying on its side" rather than the observer doing so. Note that in this position the equatorial plane cuts the observer in half - conceptually, of course: no orange people were harmed in the making of these diagrams! The observer again sees the Moon pointing directly at the Sun but this time the straight line rises at 90deg to the eastern horizon, goes precisely over the observer's head at the zenith point and carries on down to cut the western horizon, again at 90deg. The third diagram shows the intermediate case, where the observer is at 45deg latitude. The Moon now does not appear to point directly at the Sun because, as the line of apparent motion must still start at the due-East point and end at the due-West point but must also rise to be 45deg high in the South, the line is seen as curved. |
And yes, I am of course aware that in the diagrammed positions the Moon would actually be gibbous rather than crescent but I felt it was more visually-effective to use a crescent: the actual shape of the part-illuminated Moon clearly doesn't affect the argument at all.
One also can see the "curved trajectory" effect in the case of Earth satellites. If you have ever seen the ISS you will know that on some orbits it goes almost directly overhead but on most passes it only rises some tens of degrees above the horizon. In the first case its trajectory is almost a straight line but in the second case(s) it is curved. Its actual orbit clearly hasn't changed - the curvature is just an effect caused by the angle at which we see the projection of its 3D orbit onto the (apparently) dome-shaped sky. Something similar (though not exactly the same) occurs in diagrams of satellite orbits. Satellite orbits are clearly "hoops" when seen against a 3D globe, but when drawn on flat 2D (Mercator-projection) maps they have sine-curve-like shapes, as can be seen on any Mission Control display screen. While not exact analogues of the Sun-Moon illusion these examples do illustrate how lines which are straight in (one plane of) three dimensional situations can become curves in two dimensions.
Your "3 points define a plane" argument seems convincing, but this is because we are used to objects being quite close to us. The plane defined by the Sun, Moon and observer has two of its defining points (the Sun and Moon) effectively at visual infinity, despite the fact that they are really at very different actual distances from us. The apparent angular relationships on the plane are therefore distorted by the "dome & disc" perceptional illusion created by the observer, as discussed above. The truly straight line between Sun and Moon is thus actually seen as a curve. This is also why attempts to simulate the illusion by "torch shining on ball" demonstrations do not work: the true relative arrangement of the objects is quite clear to the observer and so the actual three-dimensional situation is perceived, not a "dome & disc" illusion (rather as day-time clouds tend to destroy the "sphere of the heavens" effect). It would probably be possible from considerations of optics and perception to determine how far away items have to be before they are all seen at effective infinity, thus triggering the illusion, but I think I'll leave that for another day!
I hope there's something in the above which will help you to sort out the matter to your own satisfaction, but such explanations are always difficult when they rely on the appreciation of perception rather than logic, geometry or mathematics. Either way, I have of course triumphantly achieved the previously-stated probable outcome of such an attempted explanation - I've either resolved the issue for you or have left you even more confused than you were in the first place! I hope it's the former. Do come back to me if you need another burst of grey-cell battering though!
Best regards
My Dear Holmes (!),
That is quite splendid. I wish I had thought of you earlier.
I have only read your treatise once, but follow all the points you made, and am much gratified to see your analysis of my "3 points define a plane" conundrum.
The bit I have most trouble with is your paragraph 4. Through playing around with "planetarium" software, I had already suspected that the direction that the Moon "points in" is a tangent to the curve it traces out in its passage through the sky. I could not prove this to my satisfaction however. Nor could I accept why the trajectory appears to be a curve through the sky. I can sort of "feel it" but have difficulty formalising it. Your analogies and thought experiments are persuasive.
I felt I should put it to rest. I will study your reply several more times until I am happy with it.
P.S. If I were in space in a spacesuit, facing away from the Earth, no horizons, how would I see the effect then? (This one bothers me.)
P.P.S. If it really is an old chestnut, why have I been so singularly unsuccessful in finding a sensible answer?
All the best,
Rog.
Hi Roger,
Re. your P.P.S., I can only assume that people simply won't accept the "dome & disc" explanation (as I call it) because it relies on an understanding of visual perception rather than some simple geometric theory. Other more outlandish or convoluted explanations thus tend to gain prominence in the discussion forums.
However, glad to hear I have been able to elucidate rather than obfuscate and thus resolve a conundrum which has been with you for more than 20yrs. Paragraph 4 is really the heart of the matter and I would agree it can be difficult to accept. The ability to think spatially definitely helps. The "Gedankenexperimenten", much beloved of Einstein, certainly point one in the correct direction (so to speak!!). The analogies help to show that the phenomenon is not unique to the Sun-Moon case and allow a bit of "compare and contrast" which can help with the visualisation. You are quite right though to say that, in the end, you simply have to persuade yourself of the correctness of the argument rather than work through a progression of logical statements.
As to your P.S., I think the fact that it would be obvious to you that you were floating in a void (because of your all round 360deg field of view) would completely dispel the "dome & disc" feeling. Also, because nothing would be moving across the "sky" (assuming you were not in orbit round the Earth) and there are no horizons, there would be no movement trajectories to consider - you'd just see a static geometry laid out before you in its correct 3D sense. I would thus guess that as long as you were far enough away from the Earth that you could actually see the entire scene, the illuminated part of the Moon should always appear to be directed straight at the Sun - whether or not the Earth was in your view. Rather hard to prove this though, as of course it would be almost impossible to take a picture of the Sun, Earth and Moon at the same time because, even if you could get the right viewpoint, the Sun would be just too bright to enable a correct exposure. The best I can do is offer some shots of Earth and Moon together taken by planetary probes: I've chosen those at about half-phase and with the terminator approximately upright to make comparisons easier.
 
 |
| Images of the Earth-Moon system taken by the (from left to right) Galileo, Mars Global Surveyor and Mars Reconnaisance Orbiter space probes. |
In principle, if the "dome & disc" effect is occurring, the "aim-points" of the crescents of two heavenly bodies at different y-axis positions relative to the observer should be different, as the degree of curvature of their trajectories will be different. Unfortunately, the difference in position of Earth and Moon when seen from a distance is probably too small for this effect to be reliably detected. Also, the resolution of the images themselves is quite low, leading to uncertainty as to where the line of the terminator actually is. However, for what it's worth, when I place lines against the terminators of Earth and Moon (separately for each image) in my graphics program they are pretty well parallel: try it yourself and see what you think. There's certainly no gross difference. The final test image (below) is a gibbous Moon seen behind a Space Shuttle. A gibbous Moon will give the greatest aiming error when seen from Earth, as it will be on the "upslope" of its trajectory as the Sun is on its "downslope". I think it's clear from the shadows on the Space Shuttle, however, that the illuminated part of the Moon is pointing pretty well exactly at where one would guess the Sun must be. So, not definitive in either case but certainly suggestive. Maybe we should put it forward to NASA as an experiment they might like to try!
 |
| The Moon seen from Space Shuttle Discovery |
Best regards,
Dear Sherlock, [My nickname!]
Re the P.S. If one could ignore the horizon (and clouds) then I can't see the difference between being in space and being on the Earth so why does it look so different? I suspect we're drifting into psychology here, but can you see what I mean?
However, I liked your photos. Do you mind if I discuss them a bit? As you say, they do seem to "point" in the right directions. Now I have taken some photos from my back garden of the Sun & Moon simultaneously, using a welding mask to shield the Sun. In general, due to the wide field of view it takes a few snaps to get both objects in, which then have to be stitched together. This is difficult, as without reference points the stitching is well nigh impossible. One could use the horizon, or clouds, but I suspect that both could contribute to an unintentional rotating of the images. Whatever, non-alignment of the crescent Moon and Sun is plain to see. Now assuming that image assembly IS correct, a photograph cannot know whether it is "in space" or "on the Earth". And yet your space photos show alignment, and my Earth photos show non-alignment. So (having rejected all the impossible possibilities) one is left with the conclusion that the image assembly is at fault. But that is not entirely pleasing.
Hmm. I have managed to find one of my snaps. Here it is. No it isn't - I've done better than that. I've found a version with accompanying notes!
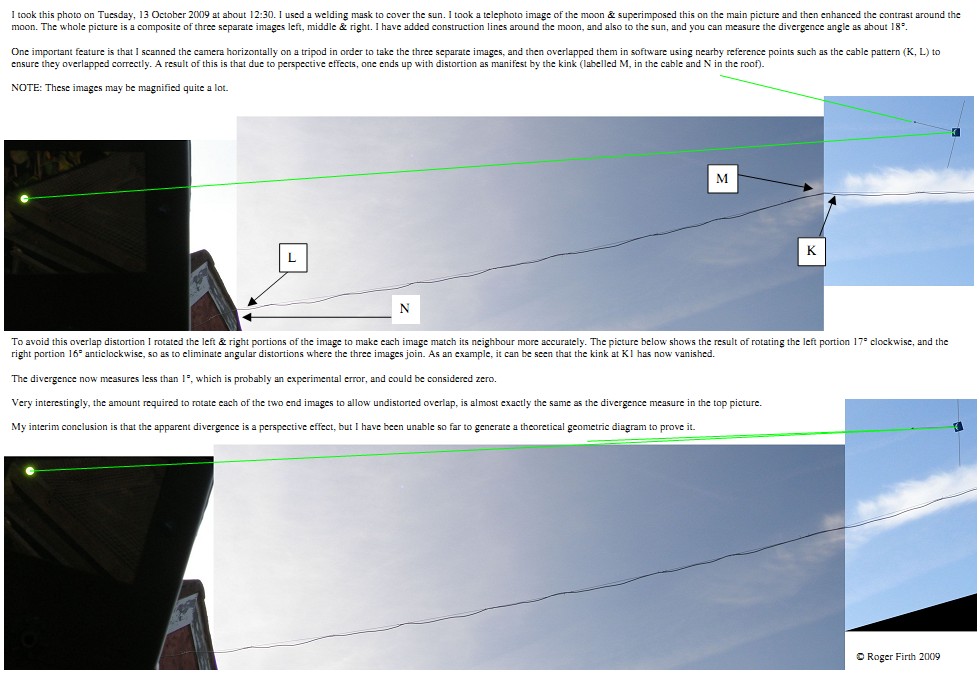
Bye for now,
R.
Hi Roger,
You've given me two rather different points to answer this time, so I'd better get on with it!
I entirely see what you mean about the difference between being on the Earth and being in space. I suspect the perceptual difference lies in the fact that in space you have an unrestricted view of an uncluttered and essentially static environment whereas on the Earth you are peering out at a very small portion of the heavens through a sort of moving pinhole which is itself surrounded by other objects very much nearer to you. As I mentioned in my first email, this causes the three-dimensional reality to be projected and distorted onto a visual field which appears to be dome-shaped, thus turning straight lines into curves. While I don't think there's an exact parallel, it may be similar to the effect you get when taking panorama photographs. As every school-pupil of a certain age is aware, the "long-strip" photos of an entire school have to be taken with the subjects assembled on curving ranks of benches in order to get a straight final result. What the camera sees is thus not what the reality actually is, because of the limited viewport of the lens compared to the much wider field of view (and different position of view) of the person watching the photograph being taken. I suspect that if you stood by the panoramic camera and scanned the scene though a small tube you would also believe that the curving line of pupils was straight.
It is interesting to note that although the "crescent illusion" generates so much discussion, people are seemingly quite happy with the fact that the Moon's path across the sky is a curve, though surely a moment's reflection would show that this cannot be an accurate representation of the actual orbital facts. Also, by watching the Moon over a period of hours you will see that it appears not only to move in a curve but also to rotate clockwise (anti-clockwise if you're in the southern hemisphere). How can this be? I would have thought that the curve plus the rotation would quickly indicate to anyone with a feel for spatial geometry what the correct answer was - the limited view given to us by a restricted viewport produces the perception of a curved two-dimensional background, onto which straight lines are projected as arcs.
If the impression of space being curved wasn't enough, you then have to add in the other factor I mentioned last time in connection with the "3 points make a plane" problem: although the Moon and Sun appear to be the same distance way (and so the triangle formed by lines running from Moon to observer to Sun to Moon seems to be isosceles) in fact the Sun is 400 times as far away as the Moon and so the illumination angle is completely different from what we think it is. This also upsets our perception of the situation. In space I think it would be much more obvious what the true position was, as we would not be deceived by the presence of the other objects we can see around us, particularly those on our local horizon, into thinking that the Moon and Sun were a) really quite close and b) the same distance away.
However - the great difference in true distances will not in fact affect the "pointing problem". A few moments thought should convince one that because the Sun and Moon lie in [very nearly] the same plane when viewed from the surface of the Earth (because they both remain within a narrow band in the sky, marked out by the Ecliptic - as explained in the next section) any disparity in their relative distances cannot affect the angle of the terminator (the division between the illuminated and dark sectors of the Moon) and thus whether or not the illuminated sector points directly at the Sun. What will be affected is the amount of the Moon's disc which will be illuminated as seen from the Earth. Simple geometry will show that at any given angle between the Earth-Moon and Earth-Sun lines, the farther away the Sun is the less of the disc will be seen as illuminated. Considering the situation where the angle is relatively small (i.e. when the Moon is a few days past New), in the "as perceived" case of Sun and Moon being at the same distance from us exactly half the Moon would be illuminated. In the actual case of the Sun being much further away than the Moon, because the Sun's light strikes the Moon mainly "from behind" we can only view just the edge of the illuminated portion, which is observed as a crescent. We therefore see that while the difference in distance is what produces the Moon's distinctive phases, it can only affect the "longitude" of the terminator, not its "tilt".
The final factor which might have an influence is that on the surface of the Earth you are inside the problem whereas in space you are on the outside i.e. "down here" we believe we are on an unmoving surface about which the Moon and Sun are orbiting whereas in space one could presumably see that the reality is a revolving Earth round which the Moon is slowly orbiting while the Sun stays fixed (I am here assuming the astronaut is in the same solar orbit as the Earth but is not a satellite of it). The entire perceived geometry is thus completely different, leading to a different mental model of the situation.
So, if we see a geometrically-distorted view of reality from the ground and "the truth" when in space, how does one change into the other? My answer would be that as we rise into space the size of our viewport increases, because the distance to our visual horizon gets larger and larger. This makes the radius of curvature of our "dome" greater and greater, which reduces the curve of any "straight" line drawn on it. Ultimately, when we have an all-round view the horizon vanishes, the radius of curvature is infinite, the "dome" effect therefore disappears and straight lines remain straight. If we were to keep an eye on the Moon and Sun while we were rising, the "aiming error" would steadily decrease as the sky-path flattened out with the increase in radius of curvature of our visual dome. When in space, the illuminated sector would truly point directly at the Sun, as the trajectory would now be defined by the (flat) plane of the Moon's orbit. One could probably test this by going up in a plane, but I'm afraid my Lear Jet is currently being serviced! I've looked on the Web for pictures of the Moon taken from aircraft but there are very few of them and those that do exist don't show the Sun as well, so the question is still open.
So, on to the second point.
Your composite photo, plus explanations, is certainly interesting as it demonstrates quite clearly that there really is an "aiming error" - it's not just a figment of the imagination of the viewer. Your Carsington Reservoir panorama also shows this very nicely, emphasising that the phenomenon occurs for all phases of the Moon and over very wide fields of view. To explore the matter further, I set up in one of my planetarium programs (SkyMap) the exact situation you describe for the composite. I did consider doing this for the Carsington panorama also, but the wide angle between Moon and Sun made this impractical - I couldn't zoom out far enough! The diagrams below are thus of the area of sky adjacent to the Sun (circle with a dot in it) and/or Moon (crescent) at the date and time you specified (12:30pm on 13th October 2009). I've removed all the stars but left in the planets to act as reference points. I've also asked the program to add in the ecliptic as a dashed line. This indicates the general plane of the solar system, and also marks the apparent yearly path of the Sun across the sky. The ecliptic does not define the Sun's path across the sky during the course of a day, but it does indicate the narrow band of sky within which the Moon and the planets must sit due to them all orbiting in almost the same plane. It is the "almost" that causes the diagrammed planets and the Moon to sit slightly away from the dashed line: in the case of the Moon, its orbit is inclined at about 5deg relative to the plane of the solar system, causing its sky-path to often be slightly offset from the ecliptic. Critically though, because the Moon always sits very close to the general plane of the solar system, the ecliptic provides a convenient representation of the straight line from Moon to Sun. It will be noted though that, like any straight line seen against the dome of the heavens, the ecliptic is curved: this is further evidence of the fact that, as stated near the top of this article, the "true" line from Moon to Sun is a curve, not the straight "A to B" line.
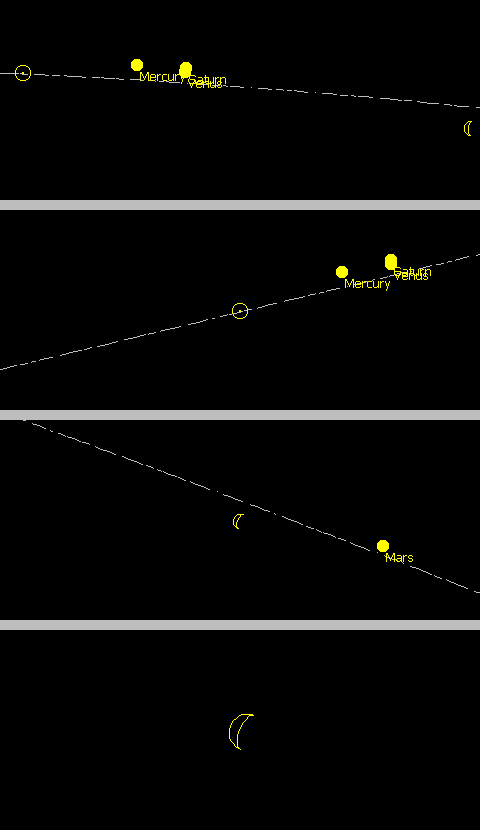The first diagram is centred on the point between the Sun and the Moon, which are separated by an angle of 62deg at this time. The second is centred on the Sun, the third on the Moon. All these three have the same [wide] angle of view (of about 65deg). The fourth one is essentially the same as the third, but with an angle of view of just 8deg to show the appearance of the Moon more clearly.
Without movement of either the eyes or the head, the field of view of the human eye-pair for stereo vision is 50 to 60deg i.e. in the diagrammed position it would not in fact be possible to effectively view both the Moon and the Sun at the same time in order to directly compare them. If it were, it can be seen that because the ecliptic is substantially flat at this particular time of day over this angle then the Moon would be seen to be "pointing" fairly well directly towards the Sun - not exactly, but not far off. This would not be true in all situations, however.
The images centred on the Sun and Moon are more relevant to the actual visual experience though, as they show that when the point of gaze is directed towards either object the ecliptic appears considerably inclined, due to the change of geometry I have referred to in my discussions (it must cut the horizon at each end, and thus must curve downwards to do so). The planetarium program calculates the change of geometry in the same way as the human perception does - it lays the 3D orbit onto the 2D surface of the sky and then allows for the fact that the sky in fact appears to be a sheet curved into a dome rather than a plane.
Relating all this back to your images, your first composite could be imitated by attaching the second and third images to the ends of the central section of the first. This will give a rising ecliptic, then an almost flat bit, then a falling ecliptic, with "kinks" at the joins (as per your overhead wire). The pointing discrepancy will then simply be the angle at which the Moon is sitting in the third (and fourth) images - this is actually almost exactly 20deg, so your measurement of 18deg was pretty close. Rotating the Moon image anti-clockwise by 17deg and the Sun image 18deg clockwise will allow the ecliptics to run at the same angle, to give a version of your second image (the wire with no kinks), in which the Moon will point almost directly at the Sun once more. The angles are not, as you found, a) the same and b) equal to 20deg because although the ecliptic is reasonably flat it is not absolutely so. The rotations thus need to be slightly different to align to the gentle curve.
[ It should also be noted that if the Moon were close to the Sun, allowing them both to be seen in the same visual field, the short section of the ecliptic connecting them would be sufficiently straight (whichever section was chosen) that the pointing error would be small and so the mis-alignment effect would not be noticed. However, this could only occur with a thin crescent Moon which would, in practice, be very difficult to see in the same sky as the bright Sun - particularly to the casual viewer. Mis-alignment is thus perhaps assumed to be universal simply because the situations when it is barely present are hardly ever observed. ]
The final two diagrams are the same situation as rendered by another program, Starry Night. Comparison of the (enlarged) image of the Moon in the "wide-angle" diagram with that in the "telephoto" view shows the different pointing angle of the Moon's crescent very clearly.
 |  |
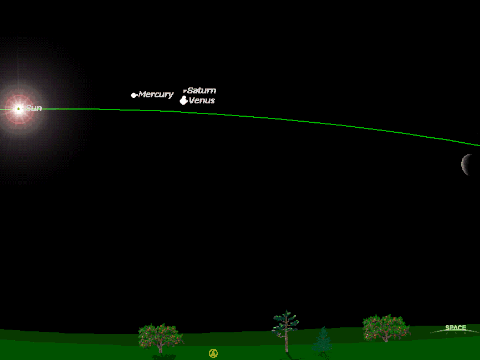Mention of "wide-angle" brings me to this image, taken from a paper on the "pointing error problem" I found on the Internet. I would give it an attribution were it not for the fact that the paper is almost impenetrable [it's a translation from an eastern-European language] and comes to a number of incorrect conclusions! It is a picture taken with a 15mm focal length fish-eye lens, showing the setting Sun at bottom left and the Moon just past half-phase at top right [the box shows the Moon at an expanded size, for clarity]. The field-of-view is thus somewhat over 90deg. It is obvious from the crane and the horizon at the bottom of the picture that the image has suffered severe spherical distortion through use of the fish-eye lens. This would normally be undesirable, but it's very helpful to the current discussion as it exactly compensates for the "dome of the sky" visual perception effect to give a situation where the illuminated part of the Moon is indeed pointing directly at the Sun, as it "should".
We thus see that theory [the programs] and practice [camera images] agree pretty closely! i.e. the effect is indeed real, but an illusion (in the sense that I shall define below) caused by a geometrical transformation. What one is doing when constructing a composite formed from rotated images is removing the curve impressed onto the "pointing path" by the change of geometry from 3D to "curved 2D": this is essentially what the spherically-distorting fish-eye lens does. The more images that are included in the composite the straighter will be the [constructed] path: the process works quite well with only 3 images in this case due to the relative flatness of the ecliptic in the particular situation used. In the limit, an infinite number of images with an infinitely small angle of view each rotated by an infinitesimal amount would generate the perfectly straight line that the path actually describes in "flat-2D". Or, working this argument backwards, the curve in the path, and hence the pointing error, is caused by each infinitesimal section of the flat-2D version of the path having to be rotated by an infinitesimal amount in order to sit on the curved-2D surface of the "dome of the sky" which is itself caused by the perception that all objects "up there" are an equal distance away from us.
You say my photos (well, the ones I found on the Internet, anyway!) show alignment but of course this isn't strictly true. They simply show that there is no gross difference between the aiming point of the half-phase Earth and the half-phase Moon: they don't show that both are aiming directly at the Sun. The point I was making was that, when viewed from the Earth, because of the "dome of the heavens" effect bodies at different angular heights above the observer's horizon will have different aiming points because their different "pointing paths" will (in general) have different slopes. If the paths are not seen as curved, however, (as per my hypothesis that the "dome & disc" effect is not present in outer space) then the aiming points will be the same. The pairs of Moons and Earths shown in the photos do indeed have different "heights" but their aiming points are the same. Conclusion - hypothesis proved. Well, not really, because (as I also mentioned) it's unlikely that the very small difference in aiming point produced by the small difference in height shown in the pictures would be noticeable in images that have presumably already been considerably expanded. The best one can say is that the pictures do not provide evidence that the hypothesis is incorrect. I thought that the gibbous Moon plus Space Shuttle picture was a bit more convincing though, as the illumination of the Moon and the shadows on the Shuttle do seem to both be produced by a light source from the same direction. We must assume that the shadows indicate the true direction of the Sun, and so the Moon does seem to be "aiming" directly at the Sun, as I would expect, rather than way off line as a gibbous Moon would be from the surface of the Earth.
Maybe a few words about my use of the terms "illusion" and "perceive" might be in order here. I am not meaning to imply that the aiming-point-error effect is simply an optical illusion or something produced by some confused mental process. The effect is real enough - the fact that it can easily be captured by a non-sentient camera is proof of that. What you see (or photograph) is not, however, an accurate representation of the in-orbit "truth". This is why I have referred to it as an illusion.
In summary, I would claim that the phenomenon is the result of three things - 1) Because all the heavenly bodies appear to be at infinity (whether viewed by eye or by camera) they all seem to be the same distance away, and are thus perceived as being on a sheet rather than in a volume. 2) This sheet is itself seen as dome-shaped, mainly due to the view-constraining effect of the visible horizon and the fact that you have to rotate your head and body to get an all-round view (as the field of view of the human eye is fairly limited). As you found when doing your composite, and as people find when doing panoramas, this is not purely a "human produced" effect but is a result of differences in perspective and angle of view as the direction of view changes. 3) When the Moon & Sun, and their daily motions, are viewed through the small "viewport" produced by the limited field of view permitted by the local horizon, and against a background which is seen as a curved sheet, geometric flat-field distortion turns lines which are straight in (one plane of) 3D space into curves in 2D space. The depth dimension has been forced to "disappear", but (except in a few special cases) the curvature originally present in that dimension is simply projected onto the two that are left, resulting in a curved path.
Rather than a single train of thought there is thus a self-reinforcing set of illusions and geometrical transformations which come together to persuade us that what we see is real:- a) the logical thought that the path must be curved because of the placement of its end and middle points; b) the geometric construct that gives a reason why the points are seen as they are; and c) the "dome & disc" illusion that produces the impression of a curved surface above us, upon which the curved trajectory would nicely sit. All satisfyingly consistent, so what we see must be the truth! However, if the scene is viewed as a wide-angle image (necessarily using optical means), the spherical distortion inherent in wide-angle and fish-eye lenses compensates for the apparent curvature of the sphere of the heavens, removing the main visual element of the argument and resulting in the Moon pointing directly at the Sun again.
I'm sure there must be a formal name for what I've been calling the "dome & disc" effect, as it is after all simply a geometric transformation of 3D space onto a curved 2D surface, as demonstrated by the sky-views given by planetarium-type programs. I think I shall stop at this point though, as I am conscious I really just expressing the same points in different ways rather than introducing anything new. So, back to you for some more comments!
Sherlock
Dear Sherlock,
Having had the benefit of your final email for around a week, I felt it appropriate to make some response.
It is gradually permeating my thick skin, and each time I come back to it seems a little clearer. The difficulty is not so much in understanding it, as accepting it. One has to keep saying, "so that is what I am looking at but this is what I am seeing". As I am sure you can appreciate, it needs to sink in. I can follow it all, and could repeat it convincingly, but I still need to believe in it!
Thank you many times over for all the effort you've made on this Sun-Moon anomaly.
After these exchanges it seemed that Roger was (almost!) convinced by my explanations. His slight reluctance to accept them, in preference to what he can actually see, is shared by many - I think this is the reason for the many outlandish "explanations" he has found elsewhere. However, while writing up our "conversation" for this article I came to the view that, in order to make what I had previously said more watertight, I would have to extend my discourse somewhat to expand upon the areas I had simplified or just glossed over. I also felt I had to address at least some of the erroneous explanations for the pointing error.
The issue that has the greatest potential for confusion is the fact that, unlike the situation described in my "thought experiment" to show that sky-paths must be curved, the Earth's axis is tilted with respect to its orbital plane. This has two main consequences. Firstly, the points of sunrise and sunset change with the seasons and also with the observer's latitude, as this determines the angle between the Celestial Equator and the observer's horizon and the angle determines the points at which the trajectory cuts the horizon. This means that the end-points of the Sun's trajectory alter their position according to the observer's location and the date rather than being fixed. There is nothing in the original "the path must be curved" argument that requires the end-points to be exactly due East and due West though, and so it still holds. However, if we wish to actually observe the Sun and Moon running along the horizon or rising at exactly right-angles to it and passing directly overhead, rather than just imagining it, we can do this only at the equinoxes. Secondly, the situation is, unfortunately, even more complicated in the case of the Moon because its trajectory depends not only on the season but also on its phase (i.e. how far it is round its orbit). This has a very important corollary: the Sun and Moon do not (except in a few special cases) have the same daily sky-path. The scope for observer confusion here is so large that I have devoted a large part of an additional page to exploring the situation (see below), as it can lead to erroneous explanations of the entire "pointing problem".
Erroneous explanations tend to fall into four camps: those that misunderstand the problem, thinking that Roger is talking about how the phases of the Moon come about; those that simply deny there is a problem (often with the use of capital letters, as in "the illuminated part MUST point at the source of illumination"!); those that make incorrect assumptions, and those that come up with an apparently plausible idea but don't test it against the facts. All four were present in the discussion forums Roger first used to explore the problem, together with just a few lone voices giving what I believe to be the correct explanation (or at least some parts of it).
There is clearly little point in me considering the first two classes of "explanation" in this article, but I feel I should examine one example from each of the latter two classes as their analyses illustrate the wide range of incorrect answers which one can encounter. However, as this article is primarily intended to explain the correct answer rather than to debunk the many incorrect ones, I have placed these discussions on separate pages. Click here to read about one "explanation" from the incorrect assumption category (which begins by discussing the "Sun & Moon don't have the same daily sky-path" issue) and here to read about one from the unchecked hypothesis camp.
After the discussions between Roger and myself had come to a natural conclusion I began to consider in more detail a statement that I've often relied upon in my explanations, namely that our view of the heavens as the "dome of the skies" transforms the planar (and thus 2-dimensional) motions of the Sun & Moon into the 3-dimensional curves we perceive them to be when seen from the Earth. This is not just a perception of course, but also an actual geometric co-ordinate transformation (as mentioned above). However, spherical geometry has never been my strongest point and so I decided to find a "qualitative" explanation rather than a quantitative one i.e. show that the observed motion must be a curve without necessarily deriving the actual mathematical equation for it. As with the considerations of incorrect explanations, this endeavour was not intended to be a part of the original article and so, again, I have placed it on another page. Click here to read it.
And then, early in 2020, Roger contacted me again to say that he had used programming techniques not available to him during the original "Moonpoint" discussions to come up with a novel geometric treatment of the situation. I thought this was a rather good demonstration of the "3D to 2D" transformations I have been talking about in this article, so I felt it should have a wider audience. Click here to read how he did it.
I hope this article has also been of interest and use to other readers! I thank Roger for engaging in the discussions related above, and also for his many helpful suggestions prior to the article being published.
