Sun-Moon Alignment - Incorrect Assumptions

In the "incorrect assumption" category we have one theory which stems from the observation that the Sun and Moon (particularly the full Moon) are often seen to be at very different heights above the horizon and apparently moving at very different angles to it. For example, at mid-summer the Sun seems to rise steeply to attain a considerable altitude before rapidly setting at, again, a steep angle to the horizon. In so doing, it traverses an extensive arc running from north of east through south to north of west. Conversely, the full Moon barely lifts itself above the tree-line before slowly disappearing, having spanned a very short arc well to the south. Given that these two trajectories are so very different, surely it is no surprise that the illuminated part of the Moon does not point directly towards the Sun?

Unfortunately for the theory, this is another of those cases where what we believe we are seeing is not actually what is really happening. To find out the reason, we first need to consider the causes of the "high-low" effect.

Most people will be aware that the motion of the stars across the sky during the night (and indeed the day, although we cannot see them then!) is due to the rotation of the Earth, and of course the rapid east to west motion of the Sun and Moon is due to the same cause. However, while the stars have essentially fixed places on the "dome of the heavens", and so traverse exactly the same arcs through the sky year after year, the Sun Moon and planets have appreciable "proper motion" i.e. they move relative to the stars. This is caused by their actual orbital motion: the Moon around the Earth and the Earth & planets around the Sun. All the planets orbit the Sun in almost the same plane, and indeed the Moon also orbits the Earth approximately in the "general plane of the solar system": this is called the Ecliptic Plane. However, because of the tilt of the Earth's orbital axis, the plane of the Ecliptic does not align with that of the Celestial Equator, as it would if the Earth sat upright (as initially assumed in my "thought experiment" diagrams near the beginning of the main article). The true situation is as shown by the next diagrams.

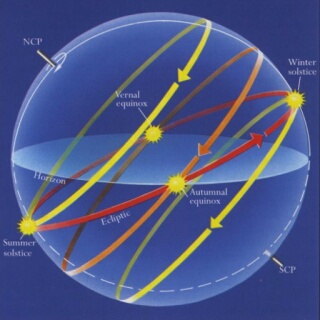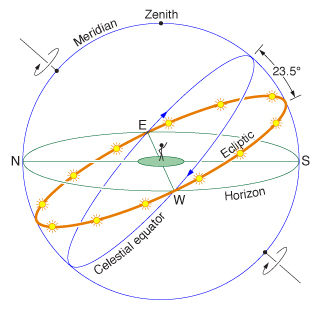
The diagram on the left (© Daniel V. Schroeder) shows the Ecliptic in its correct relationship to the Celestial Equator, the offset of 23.5deg being caused by the tilt of the Earth's axis. The twelve Sun symbols have been placed to show approximately where, as viewed by an observer on the Earth, the Sun would sit on the first of each month as its proper motion takes it anti-clockwise round the ecliptic: the one near the 23.5deg legend represents 1st January. We thus see that the Sun will be on the Meridian Circle at the winter solstice (21st December), pass the E legend at the spring equinox (22nd March), reach the Meridian again at the summer solstice (21st July) and finally pass the W legend at the autumn equinox (22nd September). The Sun's location on the ecliptic only defines its current position relative to the stars, however. To find its sky-path as seen by an observer over the course of a day we must rotate the diagram round the Earth's axis. The diagram on the right (©James B. Kaler) shows the result of doing this at the solstices (in yellow) and the equinoxes (in orange).

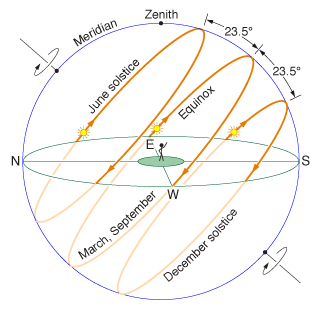If we simplify the diagram on the right above we get this one (also © Daniel V. Schroeder), which shows just the Sun's path above the horizon as seen by the observer [the diagram is not fully accurate, but is sufficiently so for my purposes at this point]. The apparent daily path across the sky of the Sun is no longer always along the Celestial Equator but rather in a plane offset to the north or south of it by an amount which depends on the season of the year. It can be seen that, as stated on the main page, this causes the points of sunrise and sunset to change with the seasons.

So, we now know why the Sun is high in the sky at midsummer noon - it is because the ecliptic sits well above the celestial equator at the summer solstice, allowing the Sun to attain a large angle of altitude relative to the observer [equal to (90-L+23.5) deg, in fact, where L is the observer's latitude]. But why is the full Moon low down? Well, because the Moon and the planets all orbit in approximately the same plane they too must keep close to the ecliptic even if they are not strictly tethered to it, as is the Sun. The ecliptic therefore defines the Moon's [apparent] orbital path through the stars in the same way as it defines the Sun's journey, though the Moon completes one circuit in a month rather than a year. By definition, the Moon is full when half-way round the ecliptic from the Sun and so if, as per the current example, we assume the Sun is at the summer solstice position then, as shown by the diagram above, the full Moon must be at the "winter solstice" position. It will thus be low in the sky at midnight because the ecliptic is then far below the celestial equator, allowing the Moon to rise only (90-L-23.5) degrees above the observer's horizon. The diurnal sky-paths of the two bodies as seen by an observer on the Earth are thus radically different even though, as shown by the full diagram to the right above, they are actually sitting in [almost] the same plane all the time - that of the ecliptic.

While the "full Moon at solstice" example is an extreme one, the general principle applies [almost] whatever the season or phase of the Moon: other than near to the equinoxes or close to new Moon the Sun and Moon tend to follow somewhat different sky-paths. However, once the effect of the change in angle of the ecliptic relative to the observer's local horizon (i.e. the variation of viewpoint of the observer) is removed it is in fact the same trajectory. An analogy might be to imagine watching a motor race from the centre of a circular track. If we stand upright, the cars will seem to pass before us at about waist height. If we now lean forward they will seem to pass at head height and if we lean back they will seem to pass close to our feet. If we continually change from "forward" to "back", the cars will all seem to be on different trajectories. This is clearly untrue, however: the paths of the cars themselves have not changed (they are still all following one another), it is our viewpoint which has shifted. While this is very obvious in the given example, it is less so when observing the skies as we are not aware of the rocking motion of our local horizon caused by the axial tilt combining with the daily rotation. We thus believe the sky-paths have changed rather than our viewpoint.

To determine whether the crescent Moon is pointing at the Sun or not one must be careful to follow the actual in-plane path between them. As mentioned on the main page, this path follows the line of the ecliptic not the path that an observer might deduce from snapshots of their sky-paths at different times of the day. The correct path can, however, be difficult to visualise in practice (as few non-astronomers are familiar with the concept of an ecliptic plane) and so the impression that the pointing direction is wrong is easily gained. However, it's probably worth re-iterating here what I hope is now quite clear by analogy with the extensive analysis I have done of the reason that sky-paths appear curved: the Line of the Ecliptic is also curved, being the projection of a flat plane onto the dome of the heavens. When moving along the "line of point" from Moon to Sun it is thus necessary to traverse a curved path, in the same way as it is when tracing the "line of movement".

In the example above we saw how the angle of the ecliptic was very different at noon (when the Sun was at its highest point) and midnight (when the Moon was at its own, but much lower, highest point). The angle clearly does not suddenly switch from one value to another but in fact varies smoothly throughout the day. This behaviour gives rise to the other incorrect part of the explanation we are considering, the theory that the crescent Moon does not point directly towards the Sun because their setting angles are different. This would seem to be perfectly obvious, but it's actually a false statement because the changing angle of the ecliptic does not affect the diurnal path of heavenly bodies. Remember that the ecliptic is the [apparent] path across the starry background that the Sun traverses during the course of a year: it does NOT indicate its trajectory across the sky during a single day. That is determined by its position on the ecliptic (which depends on the season of the year) and the rotation of the Earth.

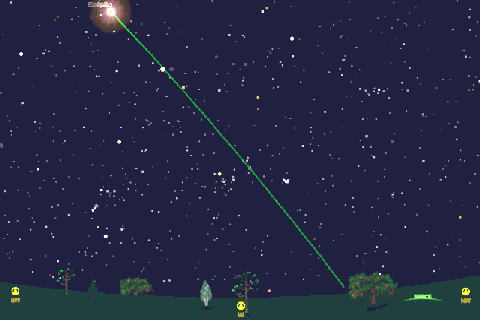To demonstrate both of the above-mentioned phenomena (the fact that the pointing direction is not [usually] in the direction of the sky-path and that the setting angles are the same), I constructed an animation which plots the setting paths of both bodies. The frames were produced using a planetarium program set for high-summer (10th July 2013, in fact, which was when I made the animation), starting at 2pm and showing the position at 1 hr intervals until the Moon sets. I set the program to ignore the effect of daylight in blotting out the stars (and often the Moon) so the true situation could be seen. The green line is the ecliptic, and the red lines show the sky-paths taken by both Sun [upper] and Moon [lower] as time passes. Click or tap on it to start it going (and again to reset).

It is clear that the line from Sun to Moon is always orientated in the general direction of the ecliptic, not along the direction of the sky-paths. It can also be seen that as the ecliptic gradually flattens out as we move towards sunset, due to the effect of the Earth's axial tilt, it takes both Sun and Moon with it, as it were, resulting in their sky-paths being curved by exactly the same amount. As we found from the previous discussion, while the Sun begins to set at a very steep angle the Moon eventually approaches the horizon at a much shallower angle. The fact that the Moon also begins to set at a steep angle would not be apparent to an observer while the Sun was above the horizon, leading to the assumption that it had been descending at a shallow angle all the time. However - their sky-paths are actually parallel and so their setting angles are equal. The same conclusions would hold when the Moon was much "older" i.e. nearer to Full, though it would be far less obvious as the two bodies would be much further apart in the sky and the Moon would set much later than the Sun. The animation also demonstrates the two reasons that the illuminated crescent is rarely at 90deg to the Moon's trajectory: the sky-paths of Sun and Moon are not often the same and the Moon's inclined orbit tends to offset it from the ecliptic. [The object between the sky-paths is Venus and the one preceding the Sun down the ecliptic is Jupiter, by the way, thus showing that the effect is not restricted to just the Sun and Moon!]

In fact, until one gets to quite high latitudes, the setting angle [or, more correctly, the solar parallactic angle] is not only equal for both Sun and Moon on a given day but also relatively constant throughout the year. It is always 90deg at the equator and has its greatest variability on the Arctic / Antarctic circles, because of course north / south of these points the Sun never sets at some periods of the year! At my location in the UK [latitude 52.3deg North] the angle varies between a minimum of 30.40deg (at the solstices) and a maximum of 37.70deg (at the equinoxes): this latter value is just 90-L, of course, where L is the observer's latitude. Therefore, in the case considered above of a solstice full Moon the setting angles of Sun and Moon will in fact be the same! (at any location). Even in the extreme case of a first-quarter Moon at a solstice the angles will, in the UK, only differ by 7.3deg. The impression that the angles can vary a great deal probably stems from the incorrect assumption that a "low" Moon rises at the same point on the horizon as a "high" Sun and therefore must do so at a much shallower angle if it is to not climb so high. Actually, it simply rises (and sets) considerably further south and thus describes an arc which is much the same shape as that of the Sun, but much shorter.

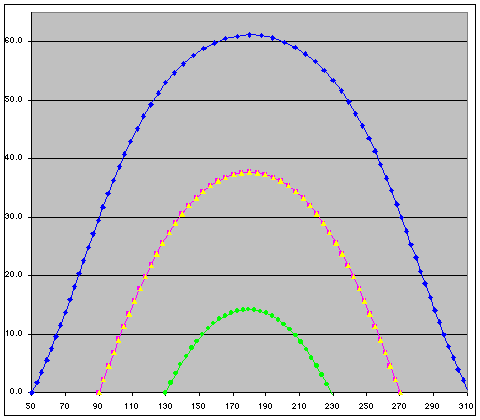To demonstrate the above points I plotted the Sun's sky-path on each of the two solstices and the two equinoxes, using data produced by the Solex astronomical calculation program for my own home location. To obtain the most accurate picture I chose years when the solstice/equinox fell as close to 12noon as possible. The results are shown on the diagram at the left: the x-axis indicates the Sun's azimuth (its angle round the horizon, where 180deg is due South) and the y-axis its altitude, at 15min intervals throughout a rise-to-set cycle. The blue graph represents the summer solstice in 2039, the yellow & purple graphs the spring equinox 2042 & the autumn equinox 2028 respectively, and the green one the winter solstice in 2041.

It can be seen that the rising/setting angles at the equinoxes are indeed equal (at 37.68deg) and those at the solstices are a) nearly equal, and b) clearly less than at the equinoxes. The solstitial angles are only "nearly" equal because of the slightly different shape of the blue and green curves. The mathematical derivation of the equation for the solar parallactic angle assumes that the Sun rises as it crosses the Celestial Equator, which of course is only true at the equinoxes. At other times the difference in length of day and night changes the geometry somewhat, leading to slightly different curve shapes and thus rising/setting angles. In the example shown, the difference between the summer & winter angles is 1.5deg but their average is 30.40deg, as predicted by theory.

It should be noted that the graphs are produced from data which does not take into account the phenomenon of atmospheric refraction: this is the "bending" of light rays due to them passing through layers of the atmosphere which have different densities. Refraction causes objects to appear higher in the sky than they really are and is particularly noticeable at the rising and setting points, when the shift is equal to the Sun's diameter i.e. when the Sun appears to be just sitting on the horizon it has in fact already completely set! This is yet another reason why the crescent Moon seems not to point at the Sun: a "non-geometric" and "non-perceptual" reason though.

The graphs help to explain why I said that the rise/set point diagrams I used at the top of this page are not quite accurate. The simplified geometry they use would indicate that the solstice and equinox trajectories are strictly parallel, which we now know is not the case, and that the shape of each trajectory will be elliptical (i.e. a circle seen at an angle, as with the rings of Saturn), which is also not correct. They do effectively capture the essential features of the situation though, so are still useful as part of an initial discussion.

It should also be noted that the graphs are strictly 2-dimensional i.e. they plot the azimuth and altitude on a flat plane, in order to make the differences between them clear, rather than on the inside of a hemisphere - the "dome of the heavens" - as they are actually seen. This is one reason why their shape is different from "beer-can" pictures, which capture the Sun's path each day with a pin-hole camera. The other is that while pin-hole cameras have a very wide field-of-view, thus enabling them to capture the entire path even at the summer solstice, they suffer from spherical distortion which changes the shape of the paths. But of course this is where we came in with this whole discussion!