 |
 |
To give a visual interpretation of the co-ordinate transformation I came up with another Gedankenexperiment. Imagine attaching a small cardboard disc (representing the Earth-bound observer's local horizon) to the surface of a basketball (representing the Earth). Now ask a helper to hold the basketball some distance from you and orientate it so that a) you can see the entire ball without changing your gaze, b) the disc is at neither of the "poles" nor on the "equator" from your perspective, and c) you can see the disc exactly "edge-on", with the disc at the top-left quadrant of the ball. With me so far? At this moment the angle between your gaze and the plane of the disc is 0deg. Now ask the helper to slowly rotate the ball anti-clockwise (as viewed from the top) around its vertical axis. The angle (measured in the vertical plane) between your gaze and the plane of the disc will slowly increase, until it becomes a maximum when the ball has been turned through 90deg. The angle will then reduce as your helper continues to turn, reaching zero again when the disc is edge-on but at the top-right quadrant of the ball.
The fact that there has been a relative change of orientation will be apparent to an intelligent ant sitting on the disc as well as to you. There is a very great difference in perception, however. From the point of view of an observer outside the system (you), it is clear that the direction of your gaze has not changed but the plane of the disc has. Conversely, the ant on the disc will believe that the plane of the disc (his local horizon) has not changed and so the direction of your gaze (and thus the direction the ant must look to see your eye) must have done. It will thus seem to the ant that your eye suddenly appeared at the edge of the disc, rose above the disc and then fell back again before disappearing at the opposite edge (the change in elevation mirroring the change in angle between your gaze and the plane of the disc). Effectively, the actual motion of the ant along a curved path (curved because it took place on the surface of a curved object - the ball) past a stationary object (you) has been transformed into apparent motion of the object along a trajectory which is curved as seen by the ant, who believes himself to be stationary. It is this transform that I am trying to determine.
Having got what seemed to be a satisfactory description of the situation from both points of view, after a little thought I decided that the analysis was best tackled by considering the "inverse problem": that is, (and here I revert to the original nomenclature) how does the view of the observer's "horizon disc" as seen from the Sun change as the Earth rotates? The angle between the line from Sun to observer and the plane of the horizon disc gives the observed altitude of the Sun, and the position of the projection of that line onto the edge of the horizon disc gives the observed azimuth of the Sun. If we know how these two vary as the Earth turns, we can determine the shape of the Sun's path as seen by the observer.
 |
 |
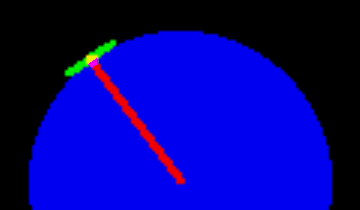
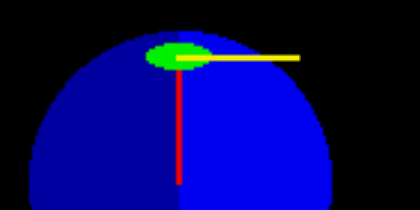
To determine these relationships I constructed animations showing views of the Earth as seen from the Sun (left) and from 90deg to the side (right), while the Earth's rotation moves the observer's horizon disc from dawn through noon to dusk. As in earlier analyses, for convenience the Earth's axial inclination is set at zero. The sphere of the Earth is shown in blue (the darker blue indicating the night side); the green ellipse is the observer's (much exaggerated!) horizon disc seen at a slant angle, and the red line runs from the centre of the Earth to the observer (and so the green disc lies at 90deg to the red line). On the side views the yellow line runs from the Sun to the observer, and on the front views the yellow blob is the Sun-line seen "end-on" and the purple line segment is the projection of the yellow line down at 90deg onto the horizon disc (the yellow line, the purple line and the red line thus all lie in the plane passing through the observer, the Earth's centre and the Sun, though it's rather hard to show this convincingly in 2D!). Colours are shown darker when they are "behind the Earth". The front view thus shows the horizontal component of the Sun's motion as seen by the observer (it is the angle the purple line has moved round the edge of the green disc) and the side view shows the vertical component (it is the in-plane angle between the red and yellow lines, minus 90deg). I hope all that is vaguely clear!
Click or tap on either animation to set it going (and again to reset). The front view shows that the horizontal component (i.e. the azimuth) starts off at 0deg (as the yellow, and hence the purple, line lies along the major axis of the ellipse at dawn) and moves progressively round the edge of the horizon disc to lie at 90deg at noon. It then continues along the horizon to lie at 180deg (once more along the major axis, but pointing the other way) at dusk. The side view shows that the angle between the red and yellow lines starts off at 90deg, increases to an angle of 180-L deg (where L is the observer's latitude) at noon, and then decreases to 90deg again. The horizon disc is at 90deg to the red line and so the vertical component (i.e. the altitude) starts off at 0deg, increases to 90-L deg and then decreases to 0deg again.
One cannot tell from these diagrams what the exact relationships between the components and the extent of the Earth's rotation are, but combining a continuously increasing azimuth with a smoothly increasing and then decreasing altitude is bound to result in some sort of arc - the result certainly cannot be a straight line. Geometry thus tells us that the Sun's path across the sky as seen by the observer must be curved. Q.E.D.
In fact, the actual data shows us that, even with a non-zero axial inclination, except at the summer solstice the azimuth varies nearly linearly with time and the altitude variation is almost a sine function. The overall path is thus close to a sine curve: this is not entirely unexpected of course, given the spherical nature of the situation. The path is closest to a sine curve at the winter solstice, because the solstice position removes the effect of the axial inclination, ensuring there is no tilt to the track as seen from the Sun - as in the animations above. The tilt present at the equinoxes introduces a small deviation from a true sine, and the path is least "sine-like" at the summer solstice, as although there is no tilt the overall geometry is rather different: for example, when viewed from the Sun the horizon disc moves uniformly "left to right" at the winter solstice or at the equinoxes but at the summer solstice it first goes "right to left" (because, as the Earth is leaning towards the Sun, the disc is on the "far-side" of the Earth at dawn), then "left to right" before going "right to left" again at dusk (I shall leave the reader to visualise these motions!). While this ensures the azimuth can traverse more than 180deg it does change the angular relationships.