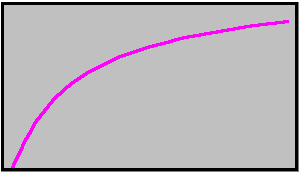

By definition, force is the gradient of the vector potential of the field being experienced. "Gradient" is just another name for "slope", and the slope of a function is found by the mathematical operation of differentiation (indicated by the symbols d/dx). That is, if P is the vector potential then F = dP/dx. We already know that the force generated by a gravitational field is inversely proportional to the square of the distance from the gravity-inducing body, so we may thus say that dP/dx = K/r2, where K is a constant [Note that I am only considering one spatial dimension, for reasons of clarity]. This equation can be satisfied if P = -K/r, which is the form of the vector potential we are seeking. If we plot this out, we get the graph on the left below: the gravity-inducing body is assumed to be off to the bottom-left hand corner. If we rotate this shape round to get the full 3-D picture the right-hand diagram shows the result, which looks rather like the "bell" of a trumpet: the gravity-inducing body would be hiding down in the throat of the bell.


We know that the force is the gradient at any point of this "potential well", so I have added lines showing the slope at a couple of typical points on the graph - click/tap on it to view them. We can see that the slope of the line, and hence the magnitude of the force, will decrease as we move away from the central body (as we would expect) but it will never entirely flatten out, let alone go downwards. The slope will thus always be "uphill" [i.e. positive] for any point on the graph. A positive slope means an attractive force, and so our initial premise is proved: a gravity field can never produce a repulsive force. This will of course also be true for the 3-D version of the graph: however we try to move away from the centre (whether directly, at a slant or in a spiral), the force we experience will always be such as to attract us back to the centre.
If we assume that the orbiting body is at a centre-to-centre distance D from the parent, because gravity has an inverse-square dependence on distance the strength of the gravitational attraction at its centre is 1/D2 times a constant formed from the masses of the two objects and the gravitational constant, G. If we now say that the distance D is in fact R times the radius of the orbiting body we can absorb the radius into the constant, so the expression becomes K/R2. Similarly, the strength at a point on that side of the orbiting object more distant from the parent (i.e. at distance R+1) is K/(R+1)2. The difference is thus K x { 1/R2 - 1/(R+1)2 }. The constant can be dropped at this stage, as it only serves to convert relative values into absolute ones. To find the extent of the differential gravitational effect we thus need to simplify the part of the expression in curly brackets.
Now (R+1)2 = R2 + 2R + 1 but if R is large we can ignore the 1, leaving R2 + 2R. If we now take out a factor of R2 we get R2 x (1+2/R). Therefore, 1/(R+1)2 is (1/R2) x (1/(1+2/R)). Considering the second part, if we multiply top and bottom by (1-2/R) we get (1-2/R)/(1-4/R2). Again, if R is large we can ignore 4/R2, leaving just (1-2/R). 1/(R+1)2 thus reduces to (1/R2) x (1-2/R), which is 1/R2 - 2/R3. Subtracting this from 1/R2 gives us -2/R3, which is the answer we require. Clearly, the difference at R minus 1 (the near point) will be +2/R3 by an exactly similar argument, but multiplying the top and bottom of the expression by (1+2/R) this time.
More generally, without having to go through the algebra again I think it is clear that for points lying a distance of r radii from the centre of the orbiting object (rather than exactly 1 radius, as used above) the difference will be +/-2r/R3, as long as r2 is much smaller than 2rR and 4r2/R2 is much less than 1. The second constraint is the more severe, requiring R to be much larger than 2r.
If we draw a line which cuts a graph at two points which are close together, the slope of the line is the difference between the values at those two points of the function defining the graph divided by the x-axis distance between the two points. If we now reduce the distance between the points, so the line eventually becomes a tangent to the graph, the slope is given by the value at that point of the differential of the function defining the graph. In the case we have been examining, the difference in values is the expression we are seeking (let's call it E) and the x-axis distance is r. We may thus say that E/r = d(1/R2)/dx. Now the differential of 1/R2 is -2/R3 and so E = -2r/R3, as previously found.
The objection might be raised here that I am equating a fraction with finite-sized numerator and denominator to a differential which, by definition, has infinitestimal elements. This is, however, only the equivalent of saying we can ignore a term in the algebraic analysis if it is much less than the other terms in the expression i.e. in both cases we are really finding what the limit value will be when the distance we are considering (r) is very small compared to the other factors in the equation.