The Tides
Prologue
When I began this particular article I had simply intended it to be a corrective for some of the howlers concerning the tides perpetrated by the BBC programme "Do We Really Need The Moon?", originally broadcast on BBC2 in February 2010. However, the more research I carried out the deeper I got drawn into the subject. I found there are enough books and websites on The Tides to fill a large room (or server!) in the British Library, but none that gives a comprehensive and fully understandable explanation which is both rigorously correct and free of pages of complex mathematics. Even those which go some way to satisfying these goals frequently fail to explain the "niggly detail", leaving the reader unsure as to how a conclusion might have been arrived at or wondering where numerical values stated as fact were derived from.
I thus decided to write an article which explored the tides from basic first principles, doing my best to ensure that every last detail along the way is fully explained. I felt it important to "dot the i's and cross the t's" in this way so the reader would be happy with the final conclusions. Some knowledge of physics and mathematics is thus assumed, but not too much I hope. However, while the article is largely complete within the subject areas it considers, to have attempted to make it an entirely comprehensive work would have been asking too much - there is a reason why all those previous books were written! The interested reader is thus invited to begin his or her own investigations after reading the results of mine.
Anyone who has read my other articles will know that I tend to place the "tricky bits" on subsidiary pages, so those not interested in the detail can skip them if they wish. In this article l have placed some mathematical derivations on separate pages, and was tempted to do the same with several major sections. Eventually however, I decided this would have resulted in too many "leaps of faith" when later topics were discussed. Accordingly, some may find it rather heavy going. Please persevere though, as it will all be worth it in the end!
Introduction
The oceanic tides are one of the most familiar phenomena on Earth, but the process which produces them is in fact a very difficult concept to explain. It seems to be self-evident that the Moon's gravity simply pulls the Earth's oceans towards it, forming a bulge of "high water" and corresponding areas of "low water". Locations on the Earth then pass through these as it rotates, causing high and low tides. While there is some truth in this explanation, the most puzzling aspect to most people is that there are actually two bulges - one adjacent to the Moon and another diametrically opposite. It is the production of these two bulges which I shall first attempt to explain. I shall then explore how moving away from a simplistic model of the Earth and its oceans introduces increasing layers of complexity to the situation before describing the actual oceanic tides and how they are produced by the processes previously described. Finally, I shall address the topic which is most intimately linked to the tides - the interaction between the spin of the Earth and the orbit of the Moon.
The key to understanding why there are two tidal bulges and not one is an appreciation of the static and dynamic forces which act in the Earth-Moon system. By "static force" I mean the force of gravity and by "dynamic force" I mean the force which acts to keep the Moon in orbit around the Earth. I shall first consider the static force.
The gravitational force between bodies
Gravity is a universal force of attraction between objects. Its strength is directly proportional to the masses of the objects (twice the mass gives twice the attraction) but falls off according to the square of the distance between the centres of the objects (twice the separation results in one-quarter of the force). This second characteristic has a very important consequence for objects whose size is not negligible as compared to their separation. Because gravity decreases with distance, the force on a particle of an object on the side nearer to another object will be greater than the force at the centre, and the force on a particle on the side further away will be less than at the centre. The difference in force varies as the cube of the distance (as I shall show at the end of this section), so even a small object will experience an appreciable difference from one side to the other.
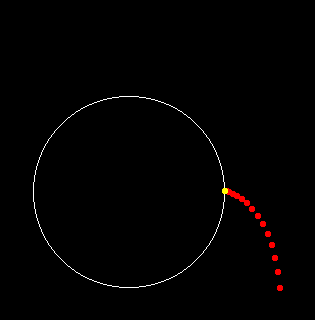
Newton's Second Law of Motion tells us that a body moves (strictly speaking "accelerates") in proportion to the net force on it. Therefore, in the above example the nearer part will want to move towards the other object faster than the centre while the further part will want to move more slowly than the centre. So, while each object will move as a whole towards the other due to the overall attractive force, because its parts are being accelerated at different rates each object also becomes elongated as it does so. An originally spherical object will thus become rugby-ball shaped, as demonstrated by this animation: the gravitationally attracting body is assumed to be off to the right. Click or tap on the animation to start. The green circle is moving faster than the yellow circles (which move at the same speed because they are the same distance from the attracting body) and the red circle moves slowest of all. The object thus moves to the right as a whole but becomes elongated as it does so. Hypothetically, an object freely-falling due to gravitational attraction towards a Black Hole would be massively elongated because of the extremely steep gravity-gradient. It would thus become exceedingly long and very thin - a process sometimes called "spaghettification"!
The above analysis considered objects which were able to move freely. If the objects are held in position by some external agent pinning their centres a fixed distance apart, they will again suffer a deformation but not the same sort. The desire of the centre points of each object to move together despite being pinned just creates a force against the external agent. However, the near and far parts can still move, so the near part becomes stretched out towards the other object and the far part is compressed against the immobile centre. The net result is that a sphere turns into a sort of egg-shape, as demonstrated by this next animation: click/tap on it to start.
In each case the actual amount of elongation or stretch & compression will be determined by the elasticity of the object. Deformation will occur until the internal tensions so created are balanced by the binding forces keeping the object together. However, the internal tensions may, if the deformation stress is large enough, be sufficient to overcome the binding forces and thus rupture the fabric of the object, destroying it. This is the origin of the "Roche Limit", which states that moons cannot orbit arbitrarily close to their parent body: get too close and differential gravitation will tear them apart.
Note that in each of the cases considered above, although the force on the parts of the objects was different, it was always directed towards the other object. Thus, although a freely-falling object will become elongated this is not caused by one side experiencing an attractive force and thus moving "inwards" and the other side experiencing a repulsive force and thus moving "outwards", but rather by different amounts of movement in the same direction. Indeed, one can easily show from basic physical principles that a repulsive force simply is not possible in a gravitational field: those up for a bit of mathematics should click here.
The inverse-cube relationship
I mentioned above that the differential gravitational force varies as the inverse-cube of the separation. This relationship can be shown by algebra, by calculus and by example. I have moved the first two proofs to a separate page: those who are interested should click here. The proof by example is illustrative though, so I have retained it within the text.
The Earth is about 60 times its own radius distant from the Moon, so let's compare the difference in strength of the Moon's gravity field at 59 radii and 61 radii (i.e at the near and far sides of Earth) with that 60 (i.e. the centre of the Earth). Gravity has an inverse-square dependence so at 60 radii its relative strength is 1/602 or 0.000277778. Similarly, at 59 radii the relative strength is 0.000287274 and at 61 radii it is 0.000268745. The magnitude of the differences of the "near" and "far" values from the "centre" value are thus 0.000009033 and 0.000009496, which are both fairly close to 2/603 (0.000009259): -2.45% and +2.56% out, respectively, in fact. [Note: the factor of 2, which comes out of the algebraic and calculus analyses]. Those who studied the algebraic analysis will know that the inverse-cube relationship only holds exactly when the orbital distance is much greater than the diameter of the orbiting object. The above calculations show us that for the Earth-Moon system a ratio of 30 (60r/2r) is "big enough" for the approximation to hold reasonably well. In fact, if we calculate what the exponent (i.e. the power of R) would have to be to give these answers the result is 2.994 and 3.006 in the two cases, compared to the "ideal" 3.000: a difference of just 0.2%. The premise that we are dealing with an inverse-cube relationship is thus very strongly supported.
Note however that the fact that the differences are not quite equal is a real effect. Although a ratio of 30 is "big enough" to prove the inverse-cube relationship, the "difference in the differences" does not fall below 0.01% until the ratio is greater than 15000. In all practical Solar System cases therefore the "near" difference will always be slightly greater than the "far" difference and so the tidal bulge closer to the source of gravitation is always slightly larger than the one further away.
The dynamics of orbital motion
We have seen that the static (i.e. solely gravitational) situation can either give us bodies with two "tidal bulges" which, being freely-moving, quickly crash into each other or bodies with a single "egg-shaped" bulge if we pin them in position. What we are looking for is a combination of the two: bodies which remain a fixed distance apart but still have two tidal bulges. The conclusion is that the dynamic part of the force beween Earth and Moon is vital in order to produce a stable situation: I shall thus now turn my attention to this aspect.
For one body to orbit another it must clearly move in a curve. However, Newton's First Law of Motion tells us that once a body is set in motion it will travel at constant speed in a straight line unless acted upon by an external force. We thus conclude that for a body to move in an orbit it must be subject to a force which acts continuously to prevent it from maintaining its "natural" straight-line motion. This force must obviously be directed towards the "inside of the curve": in the particular case of a circular orbit the force is directed towards the centre of the circle. Because of the "centre-seeking" nature of the force it is called, from Latin, the centripetal force. The faster a body is moving the more force is required to deflect it from its preferred straight line and so the more centripetal force is needed to maintain the orbit. The amount of force required also depends on the radius of the orbit: more force is needed to deflect the body into a tight trajectory than into a gentle curve. In fact, analysis shows us that the amount of centripetal force required is directly proportional to the square of the speed and inversely proportional to the orbit radius. Note also that as it has both magnitude (the speed) and direction, the motion of a body is actually a vector quantity called velocity. Acceleration is change of velocity, but the change need not be in the magnitude of the velocity: change of direction is an acceleration just as much as is change of speed. Therefore, as the direction of the velocity vector of an orbiting body is continually changing as it traverses its orbit, the body must be subject to an acceleration.
We have seen above that gravity is a centre-directed force, and so can act as the centripetal force keeping one object in orbit round another. However, I also showed that gravity alone will not produce a stable situation with two tidal bulges, so have we made any progress? The answer is Yes, of course - the fact that we are dealing with an orbiting body makes all the difference.
To maintain a stable orbit, the centripetal force must be exactly that required by the current orbital speed of the orbiting body. If it is insufficient, the tendency for the body to move in a straight line will cause it to travel in a less-curved trajectory, resulting in it spiralling outwards. Similarly, if there is an excess of force the body will be constrained to move in a tighter curve than its speed can sustain, resulting in it spiralling inwards. What is true for entire orbiting bodies is also true for parts of bodies. We saw above that the force on the side of a body nearer to the source of gravity will be greater than that at the centre of the body while the force on the side further away will be less than at the centre. It is only the centre of the body which is moving at the correct speed for the amount of centripetal force it is experiencing. All parts of the body must orbit at the same speed however, as they are connected together, so the nearer part will be moving no faster than the centre but will be experiencing a greater centripetal force. This means that the force is more than would be required to maintain a stable orbit at the current orbit speed, which will cause a tendency in the nearer part to move inwards. Similarly, the further part will be experiencing less centripetal force than would be required to maintain an orbit at this speed, which will cause a tendency in this part to move outwards. If the nearer part is tending to move further in, the further part is tending to move further out (relative to the centre) and the centre is moving in a stable orbit then the overall effect is to elongate the body in a radial direction, both towards and away from the source of gravity, without moving it inwards as a whole. This is exactly what we require for the existence of a permanent situation with a tidal bulge on the distant side as well as on the the near side. [Note that, as in the non-orbiting situation described initially, the actual amount of elongation will be determined by the elasticity of the body. Deformation will occur until the internal tensions so created are balanced by the binding forces keeping the body together].
In the case of the Earth-Moon system one might complain at this point that it's the Moon which orbits the Earth, not the other way round, so while this description can explain how the Earth produces tides on the Moon (which indeed it does, except they are tides in its solid structure rather than in an ocean) how can this effect produce the tides on the Earth? The answer depends on the fact that all orbiting systems actually rotate around their common centre-of-gravity, not the centre-of-mass of either body. If one body is very much more massive than the other it is a reasonable approximation to say that the lighter body orbits round the heavier, but the Earth is only about 81 times as massive as the Moon so this does not apply. In fact, the centre-of-gravity of the Earth-Moon system (called the barycentre) is about 2,920 miles from the Earth's centre (in the direction of the Moon, of course). This does not make much difference to the analysis given above (as the average distance to the Moon is about 239,000 miles), but means that the Earth is actually in orbit, round the barycentre. The fact that the barycentre is within the volume of the Earth (just 1,062 miles from the surface, in fact) does add a certain amount of complication, however! To begin to explore the complication we must first of all consider that often-misunderstood concept "centrifugal force".
Centrifugal force - does it really exist?
As its name implies, centrifugal force is a force directed away from the centre (as opposed to centripetal force, which is directed towards the centre). I said above that in the case of non-orbiting bodies freely-falling towards one-another there is no actual outwards-directed force causing the bulge on the distant side: it's simply that this part is falling less quickly than the centre of the body and therefore "gets left behind". In the case of orbiting bodies, however, there really does seem to be a force, exemplified by their tendency to fly outwards if the centripetal force is absent or insufficient. In reality though, there is no actual force in this case either. When viewed from a perspective outside the system it is clear that the cause of the tendency to outwards motion of that part of an orbiting body experiencing insufficient centripetal force is its wish to move in a trajectory of lesser curvature than that of the body as a whole, not because a force of some sort is "pulling it outwards". Viewed from the orbiting body, however, because there is a measurable stress on the outer part of the body some force must be postulated in order to explain it. This is the "force" known as centrifugal force: it is "real" in the rotating frame of the orbiting bodies but not for a stationary observer outside the system. This sounds like a paradox but isn't, as the comparison is not like-for-like. The frame of an observer outside the system is an inertial (or non-accelerated) frame, in which Newton's First Law holds rigorously: no change of motion without the application of a force. The frame of the orbiting bodies is non-inertial, because (as we saw above) motion in a circle requires there to be an acceleration. In a non-inertial frame there can be change of motion without the application of a force, due to the acceleration of the frame itself. This is contrary to expectation, however, and so it is convenient to postulate a force in order to give an agent for the otherwise inexplicable change of motion.
The next animations, which are drawn correctly to scale, illustrate the two different scenarios. They represent what would happen if part of an orbiting body suddenly lost all the centripetal force acting on it. This is exactly what happens when an object is whirled round on a string and suddenly released. In this case the tension in the string is providing the centripetal force, which instantly vanishes when the string is released. In the case of the animations, it is to be assumed that the object being whirled suddenly fractures, so that one part (red) flies off and the rest (yellow) remains in orbit. While gravity can never instantly disappear of course, the animations still give a good idea of what would happen if gravitational centripetal force was insufficient to maintain the current orbit. Click/tap on either to start both of them.
The left-hand animation shows the situation from the inertial frame of an observer outside the system. Once released, the red object simply moves in a straight line, continuing the motion it had at the point of release, while the yellow object continues to orbit. Nothing much to discuss there - things happen exactly how you would expect.
The right-hand animation shows the same situation seen from the accelerated (i.e. rotating) frame of an observer on the (yellow) orbiting body. In this case the red object moves directly away from the yellow object before also curving in a clockwise direction (I'll come to this bit in a moment!). The yellow object remains stationary of course - this is what is meant by "seen from the frame of ...". From the point of view of the observer on the yellow object, the fact that the red object moves away should mean it is experiencing a force - this is the centrifugal force. Given that, somewhat unexpectedly, the red object is moving away in a curve rather than a straight line, it must in fact be under the influence of two forces, not one. The centrifugal force moves it directly outwards: the force causing it to move in a curve is known as the Coriolis force. Like the centrifugal force, Coriolis force only has a reality in the accelerated frame. Its effects are real enough though - it is this force which causes hurricanes to spin and the trade winds to blow in opposite directions in the two hemispheres of the Earth.
I must again emphasise though that the centrifugal and Coriolis "forces" are not forces in a physical sense: there is no agent causing them, as there is in the case of gravity (caused by mass) or electrostatic attraction (caused by electric charge). They are simply a convenient way of describing what happens to the motion of bodies in an accelerated (which usually means rotating) frame of reference. That they are, however, equivalent to continually acting forces can be seen by combining all the frames of each animation, as I have done just below. This shows that in the accelerated frame the red object travels further in each time-step than the one before i.e. it is actually accelerating away from the yellow object. Newton's Second Law tells us that a force is needed to cause a mass to accelerate, and so the red object must be experiencing a constant force in the rotating frame. Compare this to the situation in the first animation. Here the combined frames show us that the red object travels the same distance in each time-step and so is moving at constant velocity i.e. no force is acting in the inertial frame.
Non-rotational orbit around the barycentre
So, having got that clear (I hope!) I shall return to the orbit of the Earth about the Earth-Moon barycentre. The next point to appreciate is that although it is natural to presume that orbiting bodies must always rotate about their own axes as well as around each other, this is in fact not a physical requirement. Cases where it is not true are hardly ever found in nature though (the Sun, the planets and their moons all rotate at the same time as orbiting), so "non-rotational rotation" is rather hard to visualise. An example from life would be the winding-handle on a fishing-rod reel or mechanical whisk: although this "orbits" the central drive shaft it does not itself rotate, being held in a fixed orientation by the hand of the user. For "handle" read "the Earth" and for "shaft" read "barycentre" and you have almost exactly the picture I wish to describe. There is one major difference, however: the size of the handle is much smaller than the size of the disc to which it is attached i.e. the "barycentre" lies outside "the Earth". We must therefore now imagine a huge handle, somewhat larger than the disc: this would still work perfectly well (if a little clumsily!) but the central drive shaft would now always be obscured behind the handle i.e. the barycentre is now within the Earth. This is precisely the "Earth orbiting the barycentre" situation that we want.
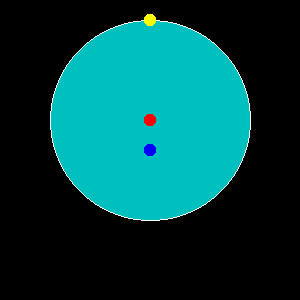
If your powers of visualisation are beginning to fail at this point, consider the next diagram. The light-blue disc represents the Earth (the very large handle!), viewed from above the north pole and with its centre-of-mass (the axle on which the handle turns) marked by the red dot. The blue dot is the barycentre (the drive shaft of the reel or whisk) - the red and blue dots would be joined by a crank of some sort in the case of our imaginary reel / whisk. The yellow dot is a point on the Earth's surface [on the equator, in fact, in this view]. Note that, for convenience, I have placed the barycentre much nearer to the centre-of-mass than it actually is. The Moon is not shown, but will be way off in the distance on the opposite side of the barycentre from the centre-of-mass.
To continue the analogy started above, if the handle is operated in the normal way by the user i.e. while keeping its orientation fixed, the red dot will "orbit" around the blue dot while the yellow dot will always remain directly above the red dot. In other words we have achieved our objective - orbital motion around an "internal" barycentre without overall rotation. To see this in action, click or tap the diagram.
 | The green circles show the paths traced by the centre-of-mass and the point on the surface. While it is no surprise that the centre-of-mass traces out a circle round the barycentre (as that is what we were trying to achieve) it is maybe more surprising that the surface point traces out exactly the same size circle. A little thought shows that this must be the case (as the yellow dot tracks the red one) but it is perhaps not immediately apparent at first glance. Note that, while I have picked a particular point in order to clearly show that the light-blue disc does not itself rotate, the "equal circle" behaviour is true for any point on the disc one might care to choose. |
| If every point is orbiting in its own circle, it must follow that, despite the fact that the disc is not rotating as a whole, each point is (in the frame of reference rotating with it) experiencing a centrifugal force. Not only that but, because the radius of every circle and the rotation rate round them is the same, the magnitude of the centrifugal force will be the same for every point. Crucially, the force on every point must therefore be equal to the force experienced by the centre-of-mass as it orbits round the barycenter (as it too orbits in the same-size circle in the same time). This is, by definition, equal to the centripetal force being exerted on the centre-of-mass, as this is the only point which is in orbital equilibrium. In addition, because each point is part of a solid body and must therefore move in a similar way to all other such points, every point will be at the same position on its own circle at any given time. This means that the direction of the centrifugal force it experiences will be parallel to the similar force experienced by every other particle, and to that experienced by the centre-of-mass. The diagram on the right shows a typical example: the purple arrows, representing the centrifugal force (which is directed away from the centre of the green circle in each case), are parallel. Not only that, they are also pointing directly away from the Moon, which is always on the opposite side of the barycentre from the centre-of-mass. |  |
So, relating this back to the Earth-Moon system, I have shown that every point within the Earth will, due to the non-rotational orbit of the Earth's centre-of-mass around the barycentre, experience an equal and parallel centrifugal force whose magnitude is given by the force of gravitational attraction of the Moon at the centre-of-mass of the Earth and whose direction is away from the Moon. However, while the centrifugal force is constant, because each point is at a different distance from the Moon the gravitational attraction on each point is different: it will be greater for points nearer to the Moon and smaller for those further away. The net force on each point will thus be directed towards the Moon for near points (where gravitational attraction exceeds centrifugal force), will be zero for points the same distance as the centre-of-mass (where the forces are equal), and will be directed away from the Moon for distant points (where centrifugal force exceeds gravitational attraction). [Note that I am still talking relative to the frame of reference rotating with each point]. Near points will thus want to move towards the Moon and distant points will want to move away, relative to the centre-of-mass.
This is, of course, exactly the conclusion arrived at after the analysis I did above for a body orbiting at a considerable distance from the barycentre. In other words, wherever the barycentre is, each of the orbiting bodies will experience forces tending to move points near to the other body even nearer and far points even further away i.e. there will be a tendency for each body to elongate in a radial direction.
There are a lot of loose ends to tie up yet, I'm afraid, but the basic conclusion is sound - a combination of the static attraction of a gravity field which varies with distance and the dynamic forces due to the orbital motion of one body round another will produce a stable situation where each body has two tidal bulges, one directed towards the other body and one directed away.
The first loose end relates to the last situation analysed. I glibly referred to "points nearer to the Moon", but of course examination of the diagram above will show that the distance between the point on the Earth's surface (yellow dot) and the barycentre (blue dot), and therefore the distance between the point and the Moon, is continually varying. The particular point is thus sometimes near to the Moon and sometimes more distant. This does not affect the analysis, however. It just means that the net forces have to be calculated and recalculated for each point at each given instant. The practical consequence of this is that the tidal bulges are not static entities, fixed relative to the Earth, but are instead "virtual" entities which travel round the Earth as different points become near to and far from the Moon. This is, of course, exactly what one would expect - the usual description is that the tidal bulges are "dragged round the Earth by the attraction of the Moon". It is, however, the bulge shapes which move round, not the physical particles. This is exactly the situation with ocean waves - the wave shape travels large distances across the water surface but the particles which comprise it at any given moment simply move up and down [well, in small circles actually due to the effect of viscous drag, but that's just being pedantic!].
Orbital motion plus axial rotation
| The next issue is the rather obvious fact that the Earth is not actually stationary - it rotates on its axis in 24hrs. Does this not mess up the nice picture of points going round in similar circles? Well, it certainly does no favours to the animations - they end up rather like something produced with a Spirograph©! So, in an attempt to avoid too much confusion, I shall start with one that simply shows a barycentric orbit plus rotation round the axis. Click or tap on it to observe that the yellow dot rotates round the red dot twice for every once the red dot goes round the blue one i.e. it simulates the Earth rotating on its axis twice for each time it orbits the barycentre. This is clearly far from the actual situation but is sufficient to illustrate what is going on without complicating the diagrams too much. |
| The next animation takes as its starting point the one above, but removes the blue colour of the Earth (to aid clarity) and adds in the circle traversed by the yellow dot. I have slowed down the animation so the position in successive frames can be fully appreciated, which is that the yellow dot moves round in a circle of the same size as in the non-rotational case but now takes two orbits of the barycentre to do so. Note however that it takes the same time to go round the circle as it did previously - the time it takes the centre-of-mass to complete one orbit round the barycentre - and so its orbital speed in the circle, and hence the centrifugal force it experiences, are the same as in the non-rotational case. |  |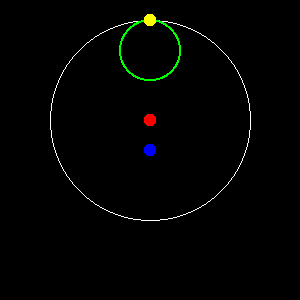
 | Finally, we have a composite image made up of every one of the eight frames in the above animation, but with the white line indicating the surface of the Earth removed (again, for clarity) and a new line added (in purple) running through the centre of each successive position of the green circle. Note that I have coloured the yellow dots on the "second circuit" slightly orange to distinguish them from those on the first circuit. If you click/tap on the image you will see a composite of all the frames, with the yellow dots numbered in sequence. The "circle within a circle" path you would trace out if you went directly from one numbered point to the next is very similar to a hypotrochoid, one of the pattern types which can be generated by the Spirograph© toy mentioned above (hence my comment). |
It should be noted that, although this is not obvious from the animations, the purple line is a circle centred on the barycentre, of radius equal to that of the Earth: this is a critical result. It shows that, although each surface point experiences an additional centrifugal force as a result of the Earth's axial rotation, the extra force is the same at each point (because the trajectory of the centres is a circle); is equal to the centrifugal force at the Earth's surface (because the radius of the circle is equal to that of the Earth), and is unaffected by the orbit of the Earth about the barycentre (because the circle is centred on the barycentre). This is what one would intuitively expect, of course: the [variable] force due to the orbit is entirely independent of the [fixed] force due to the axial rotation. One should not imagine the fixed force has no effect though: in fact it causes the entire circumference of the equator of the Earth to bulge out slightly, distorting the Earth's spherical shape. The distortion is symmetrical however, due to the equal forces, and so is not a tide-generating force.
I think you can now see why I analysed the un-natural case of a non-rotating Earth first!
Synchronous orbit
A particular case of axial rotation plus barycentric orbit is where there is exactly one rotation for each orbit: this is called a synchronous orbit/rotation. When this is so the object will always keep the same face presented to the barycentre. The next animation shows this - as ever, click or tap to start. The "circle of circles" image (on the right) shows that the yellow dot merely describes a circle round the barycentre rather than a hypotrochoid pattern. This can be confirmed by clicking or tapping on the image to show a composite of the animation frames. The green and purple circles are the same as in the previous (non-synchronous) case however: the conclusions reached concerning centrifugal force therefore still apply.
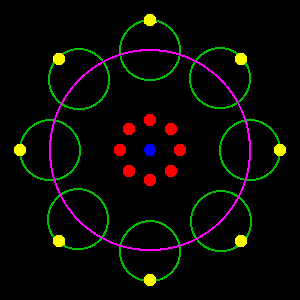
As we have seen, in the case of a synchronous orbit the surface point, the centre-of-mass and the barycentre always remain in a straight line. The other object orbiting the barycentre will always be on the exact opposite side of the barycentre from the centre-of-mass of this object, so it will never "see" the yellow dot, which will always be hidden behind the body of the first object. More importantly for our discussion, the yellow dot will always be the point which is maximally distant from the other object and the point 180deg round from it will always be maximally close. This means that the tidal bulges will remain fixed at these points: they will not move round the body as successive surface points become "far" and "near" as happens in the cases considered so far. The bulges thus become permanent distortions to the shape of the body.
If you think that an exact 1:1 ratio is very unlikely, then in one sense you are right: it would hardly ever happen by chance. However, such a ratio is in fact very common - our own Moon is the most obvious example. Because the Moon's period of revolution around its axis is exactly the same as the time it takes to orbit the Earth (as seen by an observer on the Earth), we can only ever see one side of it - the "Man in the Moon". This type of "locked" rotation is a consequence of the very tides I am attempting to explain.
Synchronous rotation comes about because of the distortions to the shape of an orbiting object caused by the tide-generating forces exerted on it by the orbited object (I here use orbiting and orbited object rather than mutual rotation about a barycentre because in the Solar System a small moon orbiting a large parent is the norm. Ignoring the barycentre effect in the case of the smaller object is thus justified). As we have seen above, in cases other than 1:1 rotation these distortions move round the orbiting body. In so doing, they squeeze and stretch all parts of the body, which generates heat due to internal friction. Heat is a form of energy, and this energy must come from somewhere. Where it comes from is the rotational energy of the body. Consequently, as the body warms up its rotation rate slows down. It continues to do this until the rotation rate is the same as the orbital period. At this point, the distortions remain fixed (as illustrated above). There is then no continual squeezing and stretching and so the dissipation of energy falls to nearly zero. The slow-down in rotation rate thus ceases, leaving the body in synchronous rotation. The "locked" situation is in fact a minimum energy state, to which systems tend to evolve.
Other "spin-orbit resonances" (as they are called) are possible, depending on the exact details of the system. For example, the planet Mercury has a considerably eccentric orbit and so, by Kepler's Second Law, its on-orbit speed varies quite a lot. For 1:1 tidal-locking to occur the spin and orbit speeds must be fairly constant, else the tidally-generated bulges will arrive in position "early" at perihelion (when the orbit speed is fastest) or "late" at aphelion (when the orbit speed is slowest), upsetting the synchronisation. However, because the tidal effect is strongly dependent on distance, for an eccentric orbit the much stronger effect at perihelion tends to dominate the weaker effect at aphelion. Given that there are two tidal bulges, synchrony at perihelion can be achieved if the body rotates 1.5 times for each orbit. This means there is a minimum-energy state before the simple 1:1 ratio is reached, at 3:2 (58.65 days axial rotation, 87.97 days orbital period) and this is exactly the situation found. Surprisingly, the correct value for Mercury's rotation rate wasn't discovered until fairly recently (the 1960's and 70's). This is because, purely by chance, the interval between occasions when Mercury is favourably placed for observation from the Earth is almost exactly twice the rotation period: the same face will thus tend to be observed each time, leading to a presumption of 1:1 synchronous rotation. It wasn't until radar observations were made (which can use the Doppler shift to detect rotation) that the true 3:2 situation was revealed.
Having analysed synchronous rotation, I must now refer back to a much earlier analysis in order to clear up a further "loose end" I deliberately left unresolved - the production of tidal bulges on a body orbiting far away from the barycentre, such as the Moon. This analysis proceeded via the consideration of the tendency of bodies to spiral either inwards or outwards if the centripetal force was more or less [respectively] than that required to maintain a stable orbit. I there spoke about "the side of a body nearer to [and further from] the source of gravity". The implication was that this "side" was always "nearer to" or "further from" the source of gravity: we now know that this will only be true if the orbit is synchronous. For non-synchronous rotation the part of the body "nearer to" and "further from" will change at each moment. This will not affect the analysis at all though, as I showed in the case of the Earth. It will just mean that the elongations caused by the tendency of points to move either inwards or outwards will travel round the body as it turns rather than existing at one place on the surface, again just as in the case of the Earth. It was, however, convenient for me to ignore this nuance until the "close to the barycentre" case had been analysed.
The same or different? Frames of reference and Free-fall vs Orbit
Which also brings me to an issue some readers may now be considering - "how come the tidal bulges on bodies orbiting far from the barycentre are caused by the tendency for orbits to spiral in or out while those on bodies where the barycentre is within their own volume are caused by the balance between the gravitational and centrifugal forces?". The answer is that these two processes are actually one-and-the-same: the difference in the descriptions is just a question of the frame of reference being considered. In the first case, it was convenient to view the system "from the outside" i.e. in an inertial frame. In this type of frame centrifugal force has no reality and so the description relies on the tendency for objects to move in a straight line if there are no forces on them. In the second case, due to the complex nature of the various rotations caused by a barycentric orbit, we had to view the system "from within" i.e. in a non-inertial frame centred on a particular point which was rotating relative to the barycentre. In this type of frame it is convenient to use the concept of centrifugal force, so I did. It would easily have been possible to use a rotating frame plus centrifugal force in the first case, but I didn't want to base both explanations on a force which doesn't actually exist! I thus used an explanation based on orbital dynamics. Conversely, to use this type of explanation in the barycentric case would have been more confusing than the centrifugal force explanation. So, it's just a case of "horses for courses" rather than two different physical processes.
Now is also the time to consider the other "same but different" issue raised by these analyses. Almost at the beginning of the entire discussion I showed that gravitationally-attracting objects in free-fall towards each other will develop tidal bulges on each side due to the [tendency for] different amounts of relative motion of their constituent parts in the spatially-varying gravitational field. The later analyses then showed that similar bulges will be formed if the two bodies are in orbit around each other, due to the imbalance between the centripetal and centrifugal forces. The major difference between these cases is that the orbiting situation is stable whereas "mutual free-fall" clearly isn't. The big question is whether they are separate phenomena or the same phenomenon viewed from two different perspectives. Let's try an algebraic approach first.
In the free-fall case, the greater tendency for inwards motion of the "near point" is due to the difference in gravitationally-produced force on this point as compared to that at the centre of the object. We may thus say that F(near) = G(near) - G(centre), where G is the gravitational force. In the orbital case, there is also a force difference, but this time between the gravitational force and the centrifugal force i.e. F(near) = G(near) - C(near), where C is the centrifugal force. I also showed that the centrifugal force is, rather unexpectedly, the same for every point in the orbiting body and, in particular, equal to that at the centre point. We may thus say that C(near) = C(centre). However, we know that at the centre of the orbiting object the net force is zero, as this point is in a stable orbit. Therefore, 0 = G(centre) - C(centre) i.e. C(centre) = G(centre). So, substituting these results into the equation for the orbiting body, we get F(near) = G(near) - C(centre) = G(near) - G(centre), which is just the equation for the free-fall case. In other words, Yes, the two cases are basically the same thing. Note though that I used centrifugal force in the derivation. One can thus only say they are the same when viewed in the frame of reference of the orbiting or free-falling body. An external observer can easily see the difference between orbiting and free-fall (in particular, that there is no actual outwards-directed force present in the orbiting case) and so would tend to view them as separate, though related, phenomena.
The above result does raise an interesting question though. If, in the frame of reference of the body, the orbit and free-fall cases are indistinguishable, does it mean that, in some sense, orbit is free-fall? Again, the answer is Yes. To see why, imagine a cannon firing a projectile straight up in the air (a rather dangerous thing to do, but this is only a thought experiment!). The force of gravity will cause the upwards speed of the projectile to steadily decrease as it rises, until it comes to rest for a split second before falling back to Earth. When falling back, the situation is exactly that which we have been considering for two mutually-attracting bodies i.e. the projectile is in free-fall. Now imagine that the cannon is aimed slightly off the vertical. The upwards part of the projectile's motion will be exactly the same but the horizontal component of its motion will ensure that it lands some distance away from the cannon. What happens as the cannon's aim-point is made lower and lower? The horizontal component of the projectile's motion will become greater and greater and so, at first, it will simply land further and further away from the cannon. However, eventually the curvature of the Earth will become significant. As the Earth's surface falls away from the projectile as it descends, the distance it travels rapidly increases until, at a critical point, the surface will be falling away at exactly the same rate as the projectile is descending. At this point, the projectile never hits the surface and so continues round the Earth: it is thus now in orbit. The fact that it is in orbit is [almost] entirely due to the horizontal component of the motion, however: the vertical component acts in exactly the same way as it did in the "cannon pointing straight up" case. Therefore, although it doesn't look like it, the projectile is indeed actually in continuous free-fall while orbiting, exactly as it was when travelling straight down. The only difference is that the orbital motion ensures that the free-fall never results in an impact.
That this is so can be seen in a practical example. Anyone who has ever seen TV pictures from the International Space Station will know that objects inside it are weightless, and thus float around rather than falling. How can this be? Well, assuming no-one has suddenly invented an anti-gravity machine, the reason is that the constituent parts and contents of the ISS are mutually in "orbital free-fall" and are thus all falling towards the Earth at the same rate. If there is no velocity difference between two objects they will stay in the same place relative to one-another and so if one object is, say, a table and the other is a pen placed a short distance above it then the pen will stay "floating" above the table instead of falling onto it as one would expect i.e. the pen has become weightless relative to the table. True weightlessness requires a perfect balance of forces, however, which is unlikely to be the case in practice due to slight variations in the orbit from moment to moment. Also, we must not forget the variation in gravity across the ISS - despite its small size as compared to, for example, the Moon this will still be appreciable because of the inverse-cube relationship with orbital distance. Indeed, satellites are often stabilised in orbit by "gravity gradient" means, with weights on long booms providing a slight force due to differential gravity which counter-acts any tendency for the satellite to oscillate out of position. Both variations are small in absolute terms but even so they mean that true weightlessness is not possible, hence the use of the term "micro-gravity conditions" instead.
The tide-generating force on a spherical body
In my analyses so far I have only really referred to the magnitude of the forces experienced by points within the orbiting bodies: the assumption has been that all forces will act directly along the line joining the centres of the bodies. However, almost all the points will lie "off-axis". Because gravity acts "point-to-point", the gravitational force will be directed along the line from each individual point to the centre of the other body, not along the line running between the centres of the bodies as a whole. Also, although all points will experience the same "differential gravitational force" effect, because they are not all the same distance from the other body the magnitude of the differential force will not be quite the same in every case. On the other hand, I showed that the centrifugal force on each and every particle is a) the same, and b) parallel. So, when the gravitational and centrifugal forces are subtracted from each other their net effect will vary both in magnitude and direction when "off-axis" points are considered. This makes the actual distribution of the tide-generating forces around a spherical body very different from the simple cases considered so far.
In the case of the Earth-Moon system, at the points which are maximally "off-axis" (i.e. those at 90deg to the near and far points) the gravitational force will act at 0.9495deg to the centre-to-centre axis, and this value will decrease as we move towards the axis. Surely this is too small to make any difference? No - it is the very fact that the angle is small (but non-zero) that makes it significant when subtracting two forces which are nearly the same. If it was literally zero, then the resultant force would clearly always be along the axis. If it was large, the net force would be at some large angle to the axis, but it would take a considerable change in the magnitude of either force to alter this angle significantly. When it is small, however, a very slight change in either force can swing the direction of the resultant force by a large amount.
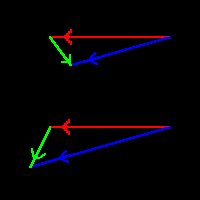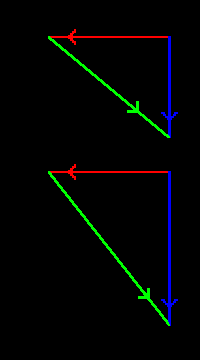  | This is best seen by means of some diagrams: vector diagrams, in fact, as on the left. In each diagram the red vector represents the centrifugal force, and is the same in each case. The blue vector represents the gravitational force: it is somewhat greater in the lower diagram of the pairs, but each blue vector on the right is the same size as the corresponding one on the left. The green vector represents the difference between the red and blue vectors.
It can be seen that when the red and blue vectors are at a small angle to each other the slight change in magnitude of the blue vector makes an enormous difference to the direction of the green vector. When they are at a large angle however, the change makes very little difference. It should also be noted that when the angle is small the resultant is much less than either of the original forces: this will become relevant later on in the discussion. |
To see what the effect of this sensitivity might be, I calculated the magnitude and direction of the tide-generating force (gravitational minus centrifugal) for a number of points at different latitudes on a line of fixed longitude (e.g. the Greenwich Meridian) on the side of the Earth's surface facing the Moon, taking into account the variations in distance and angle already mentioned. Because I was now taking both magnitude and direction into account, the subtraction had to be done on a vector basis of course (as per the diagrams above). I then repeated the calculations for a similar line of points on the far-side. The important results arising from these calculations are as follows:-
- The numerical values for the near-side and the far-side are very similar but slightly different, reflecting the difference in the tidal forces on the two sides shown in the worked example given near the start of this article. The direction of the forces on the far-side was reversed from those on the near-side, though, as would be expected.
- While the direction of the force at the near and far points is exactly along the axis, at the maximally off-axis points (i.e those at +/-90deg latitude) it is at 91.4deg i.e. almost straight into the surface! Rather surprisingly, the magnitude of the inwards force at these points is exactly half of the outwards force at the near and far points.
- The angle of the tide-generating force steadily swings round as one moves to lower latitudes, eventually emerging from below the surface in order to be pointing directly away from it when 0deg latitude is reached. There is thus a point at which the direction is just tangential to the Earth's surface: this is at 54.7deg (average of near-side and far-side values). The magnitude of the force increases from pole to equator, to reach its maximum value at 0deg latitude.
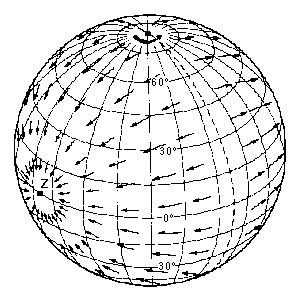
 | All this is better seen graphically though, so I've converted the numbers into a diagram, left, which is drawn accurately to scale. The yellow lines show the direction and relative strength of the tide-generating force at 10deg intervals of latitude, and the white arrow indicates the direction of the Moon: the cross on its tail marks the centre of the Earth. Click or tap on the diagram to switch between "Moon to the right" and "Moon to the left", in order to appreciate the difference in the near-point and far-point forces: successive clicks/taps switch back-and-forth between the two. |
The formation of the tidal bulges
We are making good progress, as it seems we can now actually see the tidal bulges. It would appear to be obvious that the variation in strength of the tide-generating force with latitude must pull up the oceans by different amounts, thus producing the shape of the bulges. Unfortunately, as is often the case in life, this simple answer is completely wrong! While the tide-generating force looks impressive in diagrams, it is actually puny. This is because the gravitational and centrifugal forces very nearly balance and are very nearly in exactly opposite directions. As we saw with the vector diagrams above, the result of their subtraction is thus small: in fact it is only 1.15x10-7 of the force due to gravity at the Earth's surface! This is clearly insufficient to pull up a tidal bulge, so what does produce them?
The key to the "bulge-forming" mechanism is the observation that, as can be seen from the diagram, the direction of the tide-generating force is not constant relative to the Earth's surface. In general, it will thus act not just vertically but also horizontally: indeed, at the 54.7deg point it will act only horizontally. We have seen that the vertical component cannot produce a bulge but the horizontal component can, albeit by a different mechanism.
Water, like any fluid, will flow very readily in response to even a slight difference of pressure. The magnitude of the horizontal component, like the total tide-generating force, varies with latitude. Importantly though, its direction is constant - from "pole to equator". There will thus be a constant pressure gradient in this direction, which will tend to cause a movement of the oceans in response. The horizontal component, which is often called the "tractive force", is virtually zero at 90deg (as the direction of the tide-generating force is almost straight into the surface), grows steadily towards a high point of 75% of the maximum tide-generating force at 45deg, and then decreases to zero again at 0deg (as the direction of the tide-generating force is now directly out of the surface). An element of water near the poles will thus be drawn towards lower latitudes increasingly strongly until, having passed the 45deg point, it will experience a slowly reducing force as it approaches the equator. It will still keep moving, however, due to the overall pressure gradient and so it will join the other similarly-attracted elements which have been dragged here, all piling up to form a tidal bulge. We thus see that the bulges are actually "pushed up" rather than "pulled up"!
The above analysis for numbers of points of different latitude on one fixed line of longitude can of course be repeated for any set of points circling the centre of the Earth. The most obvious other case which springs to mind is points of different longitude on one fixed line of latitude e.g. points round the Equator, but any circle of points inclined at an angle to the Equator would do just as well. If we assume that the Earth is a perfect sphere, the angular geometry is the same in all these cases and so the maximum value of the tractive force is not just at a point but along a circle. Similarly, there is zero force not just at one point 90deg away from the point closest to the Moon but in a circle along an entire line of longitude. The net result is the distribution of force shown in this diagram.
The letter "Z" indicates the point nearest to the Moon and the arrows represent the strength and direction of the tractive force. The dashed line shows where this force is zero. It can be seen that, because of the symmetrical nature of the situation, all the arrows converge on point Z. All the elements of water drawn by the tractive force on this side of the globe would thus converge on this one point, creating a single tidal bulge. There would of course be an equivalent bulge on the other side, drawn up by the components of the tractive force heading away from the zero-force line.
Once a bulge has begun to form, the water at the top will clearly be higher than that part-way down the bulge (as viewed from the perspective of an observer on the equator) and so it will have a tendency to flow back "downhill" again under gravity, thus levelling out the bulge. It would have to run down the slope of the bulge to do so, however, which would cause it to move very slightly towards higher latitudes and/or longitudes. We know that, in so doing, it would encounter an increasingly strong tractive force dragging it back to the bulge again. The situation is therefore dynamically stable and so, once formed, the bulges will persist even in the face of perturbing forces which might disturb them.
The shape the bulges take up is determined by the balance between the tractive force trying to pile them up and the gravity field of the Earth trying to smooth them out again. By applying the mathematics of fluid dynamics to the situation, it is possible to derive an equation describing the shape which the water takes up when the tractive and gravitational forces are in equilibrium - the so-called "equipotential surface". This turns out to be a remarkably simple formula, which in the 2D case analysed initially is H = K x (cos2L - 1/3), where H is the height of the bulge above mean sea-level at latitude L (specified in radians) and K is a constant whose value is determined by the size and mass of Earth and Moon and the distance between them. As long as the mean sea-level is considerably greater than H, this equation defines an oblate ellipsoid, which is just a formal name for the familiar "double-ended egg" shape usually seen in diagrams (which often show the bulges as far too "pointy", however!). The equation tells us that the two bulges at 0deg & 180deg (which create high-tides) are raised above the mean sea-level by twice as much as the depressions at +/-90deg (which cause the low-tides) are below it. At 54.7deg latitude there is no elevation or depression - it remains exactly at mean sea-level. [The mathematical reason for this is that when L=54.7deg (or 0.9552 radians), cos2L=1/3 and so H is zero]. When I made this calculation, and found it to be exactly the value given by my studies of the geometry of the tide-generating force, I definitely knew I was on the right track!
The equipotential surface is not just a mathematical concept, however. It can also be derived directly from the tide-generating force diagram by "joining up" the tips of the vectors defining the strength and direction of the force over the Earth's surface. The curve thus formed crosses over that defining the Earth's surface at the 54.7deg point of course, confirming the geometric importance of that latitude.
It is this joining-up process that tends to generate the "too pointy" diagrams mentioned above, however. In order to illustrate the variation of the tide-generating force, it is usually shown by means of reasonably long lines (as I did in my diagram, above). When the tips of these lines are joined up the result is a highly-exaggerated version of the truth - much nearer to an "airship" shape than an egg! The actual "bulges" are miniscule in real terms. In fact, the theoretical maximum amplitude of a lunar gravitational tide in deep mid-ocean is only 67cm (26 inches): the tides on the shore can be much greater of course, but this is because of local factors such as way the shape of the coastline funnels the water. We must also not forget that the Moon raises tides in the solid body of the Earth just as much as it does in the oceans. The maximum size of the lunar tides raised in the solid body of the Earth is in fact 47cm (18.5 inches): surprisingly large in comparison with the oceanic tides. To put this into perspective however, the height of the equatorial bulge caused by the Earth's rotation is 23 kilometres! (14 miles). This is still only 0.4% of the Earth's radius though.
Having steadily moved the discussion away from "the general case" towards considering the tides raised on the Earth by the Moon, there's one more aspect I need to discuss before attempting a summary of where we've got to so far.
Lunar and Solar tides
Up to this point I have assumed that all the systems being analysed are distant from any other influences. While this is fine for "the general case", it is clearly not true for bodies in the Solar System. In particular, the influence of the Sun can never be ignored. While it is 389 times as far away as the Moon, its mass is 27million times as great! We know that the tide-generating force is proportional to mass and inversely proportional to the cube of the distance, so putting in the numbers we find that the [theoretical] ratio is 0.459 i.e. the solar-induced tides are just less than half as great as the lunar-induced ones. The two are independent of each other of course, so their effects will add when the Sun and Moon are aligned (at New or Full Moon) and subtract when they are at 90deg to each other (at First or Last Quarter). These circumstances give what are called Spring and Neap tides respectively, with Spring tides being 2.7 times as strong as Neaps [ calculated as (1+0.459)/(1-0.459) ]. At intermediate positions the resultant tide will be part-way between the two extremes. Note that "Spring" has nothing to do with the season of the same name - Spring tides occur throughout the year. It probably refers to the sea "springing upwards" towards the land. "Neap", by the way, comes from an Anglo-Saxon root meaning "lacking" or "scanty", and "tide" from another such word meaning "a period of time" (as in Easter-tide).
The diagram below shows the relative sizes of all these combinations of tides, plus an animation showing how the combined tide changes as the Moon orbits the Earth: the Sun is assumed to be off to the far left (or right) of the diagram. The shape of the bulges is much closer to reality than in most diagrams of this sort, but is still hugely exaggerated. The "Moon only" and "Sun only" cases will never occur in practice of course but are shown for sake of comparison: the yellow dot indicates the 54.7deg latitude point, which always remains at mean sea-level in these cases. Click or tap on the buttons to see the appropriate picture.
It can be seen that, except in the case of Neap tides, the height of high-water is twice as great as the depth of low-water, as mentioned above. The diagram also illustrates the interesting characteristic that Neap tides have almost no actual low-water. Its level is composed of the high-water level of the Sun minus the low-water level of the Moon, the former being (as calculated above) 45.9% of the high-water level of the Moon and the latter exactly half (50%). The overall sum is therefore almost zero (just -4.1% of high-water level, in fact), meaning that low-water is barely lower than the mean level.
Interim Summary
After ploughing through all the above analyses we may say that when two gravitationally-attracting bodies are orbiting about their common barycentre, the fact that each induces in the other two tidal bulges rather than the single bulge one might expect is entirely due to the variation of the gravitational force with distance. The orbital motion plays no part in the formation of the bulges, whether the body in question is orbiting far from the barycentre or near to it; whether the barycentre is "in free space" between the bodies or within the volume of one of them, and whether either or both of the bodies is rotating about its own axis as well as orbiting the barycentre. However, while the orbital motion does not produce the bulges it must be present in order to stabilise the system: a non-orbiting system is not stable. It is therefore untrue to say that the presence of tidal bulges is entirely un-connected with the orbital motion, as some texts claim. Its contribution is indirect, but vital.
However! While the analyses show how the tidal bulges are formed, this is by no means the whole story as far as the tides themselves are concerned. There are many factors which conspire to make "real life" very far from the theoretical perfection considered so far, but there are four of particular importance.
- The Earth's axis of rotation is tilted at about 23.4deg from the vertical but the tidal bulges sit almost in the plane of the Earth's orbit.
- The plane of the Moon's orbit actually sits at about 5deg to the plane of the Earth's orbit (hence the "almost" above).
- Because water has non-zero viscosity, there is a natural limit to how fast it can be forced to move.
- As if all the above was not enough, the real Earth has a very obvious difference from the models used so far - continents!
These factors mean that the theory of tidal bulges I have described up to this point requires modification - serious modification in some cases! - to align it with what is actually seen on the Earth. We must therefore move away from the "Equilibrium Theory" we have been dealing with so far to investigate successively more representative descriptions.
Diurnal vs. Semi-Diurnal
The first modification is a relatively minor one, to allow for the fact that the Earth's spin axis is not upright (as assumed by the simple Equilibrium Theory) and so the bulges will rarely sit exactly on the equator. The consequence of this is that, as it turns with the Earth, a point at a given latitude will pass through a different part of each bulge. The two tides it experiences during a day will thus be of different heights, as the depth of water experienced by the point depends on how near to the centre of the bulge it passes. This is called the diurnal ["daily"] variation of the tides. The variation is itself variable, as the mis-match in tide heights depends on the Earth's position on its orbit. It is greatest at the solstices (when the bulges are maximally far from the equator) and zero at the equinoxes (when the bulges sit on the equator).
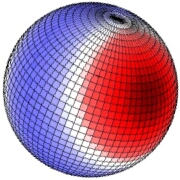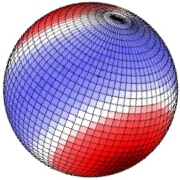  | This effect is illustrated by the next pair of diagrams [from Wikipedia], which show the solstice tides on a tilted Earth (red=high water, blue=low water), with views 180deg apart. It can be seen that the equator experiences a reasonably high tide on both occasions, as it lies in the "mid-red" area in each case. Moving north, a point sitting in the dark-red area on the left (and thus experiencing the greatest high tide) is in the white sector on the right 12hrs later, and so has no "high" tide at all, while somewhat further north there is just one short-duration high tide and one long-duration (and deep) low tide per revolution. |
The consequence of the tilt is thus to introduce a diurnal variation into the tides as well as the semi-diurnal ["twice-daily"] variation caused by the presence of the two tidal bulges. Indeed, as the diagrams show, it is possible to have fully diurnal rather than semi-diurnal tides in places. The mis-alignment of the plane of the orbits of Earth and Moon produces a similar tide-varying effect to that produced by the axial tilt of the Earth, but over a lunar month rather than a day.
Dynamic Theory
The Equilibrum Theory assumes that the substance being tidally affected can achieve equilibrium with the tide-generating force - hence its name. It also implicitly assumes that the rotation of the body does not affect the equilibrium distribution. The first is only possible if the substance can move as fast as the force is dragging it, the second requires the tidal bulges to be able to move across the surface of the rotating body without hindrance. These requirements, in their turn, need a disturbance in the substance to be able to move through it very quickly and there to be little friction between the substance and an object moving through it. The substance must therefore have a high rigidity but a low viscosity. Unfortunately, these characteristics are mutually exclusive!
In the case of the Earth, its solid body and the oceans upon it have very different values of rigidity and viscosity: they are both high for the solid body and both low for the oceans. The low rigidity of water means that near the equator the rotation of the Earth under the tidal bulges is trying to create areas of high and low water faster than the oceans will actually move. This mis-match has the surprising result that, in the absence of other factors tending to upset this simple picture, the tidal bulges will sit 90deg away from the direct Earth-Moon axis rather than in line with it i.e. there will tend to be a "trough" under the Moon rather than a bulge, giving low water when the Moon is overhead rather than high water. As we move to higher latitudes the tidal crest has less far to go (as the circumference of the Earth decreases at higher latitudes) and so eventually it will be able to keep up with the Earth's rotation. The tidal bulges will then switch to sitting in the position given by Equilibrium Theory - directly on the Earth-Moon axis - and so the tides revert to the expected pattern of high water when the Moon is overhead. Anyone who fancies investigating this odd result with a bit of basic physics should click here.
The consequence is that, in principle, regions of "inverted tide" (e.g. low water at Full Moon) will exist in a wide band straddling the "tidal equator" (the line defining the track of the bulges across the Earth's surface as it rotates). Further north and south - at places greater than 64deg away from the tidal equator in fact - the tides will revert to being "direct" (e.g. high water at Full Moon).
The very much higher rigidity of the solid body of the Earth means that disturbances can travel through it much faster than through water. A freely-propagating solid tide can thus move much faster than an ocean tide: in fact, it can travel round the equator in less than 2hrs! This is demonstrated every time there is an earthquake, when the seismic waves (which are just like solid tides) travel across and around the Earth very rapidly. Any resultant tsunami, by contrast, moves at the speed of the freely-propagating oceanic tides we have been considering (400 to 500mph). Thus, while the Dynamic Theory applies just as much to the solid tides as to the oceanic ones, their greater propagation speed means they can easily "keep up with" the tidal-generating forces and so all solid tides are in fact "direct" i.e. the bulges in the Earth's surface are always directed towards and away from the Moon, exactly as in the conventional picture of ocean tides.
Viscosity vs. Friction
Moving on to the effects of viscosity, this comes into play because of the relative motion between the quasi-stationary tidal bulges, which are "held in place" by the gravitational attraction of the Moon, and the rotating surface of the Earth. I said "quasi-stationary" because (as mentioned earlier), although the raised shape of the bulge is stationary, the actual particles which constitute the bulge are changing from moment to moment. Whether they come from the solid body of the Earth or from the oceans, particles are brought in at the "leading edge" by the rotation of the Earth; they move up the bulge, over the crest, and down the other side (under the influence of the tide-generating force), and finally leave the bulge at its trailing edge. The bulge-shape itself is thus something of a virtual object: stationary, while the particles out of which it is made are in continuous motion. This picture should be compared with my descriptions of the formation of the tidal bulges at the beginning of this article, where I said that while there was always a point on the Earth which was nearest to the Moon, it was not the same point all the time. As the Earth rotates, a given point moves away from the "nearest to" position, to be replaced by its neighbour. The concept of "nearest point" is thus constant but the actual point is not.
As the particles traverse the bulge they undergo changes in both the magnitude and direction of their motion. This requires energy to achieve, which is taken from the rotational energy of the Earth. The Earth thus experiences a retarding force, the magnitude of which is dependent upon the energy needed to move the particles around. The physical parameter which quantifies this is the viscosity - a measure of the resistance to motion of the substance, or of the ease with which another object can move through the substance. The force experienced by the Earth is thus called "viscous drag". The amount of viscous drag actually experienced is determined not just by the viscosity of the substance, but also by the flow regime of the particles: whether they are moving smoothly (laminar flow) or chaotically (turbulent flow). Much more energy is dissipated by turbulent flow than by laminar flow. Whether flow is laminar or turbulent depends (other things being equal) on the ratio of the density of the substance to its viscosity - a high ratio indicates laminar flow. Scaled to a value of 1 for water, the ratio for such things as tar and resin is in the thousands even when heated to 700C or so. One can imagine that the ratio for the solid Earth would be much higher still, and so it is almost certain that flow in the oceanic tidal bulges is turbulent while that in the solid tidal bulges is laminar.
I have described the process of viscous drag in great detail because it is necessary to distinguish it from simple frictional drag. Frictional drag occurs when a moving surface "rubs against" a stationary surface. The microscopic imperfections in the two surfaces tend to "snag" against each other, and the atoms of each substance attract each other momentarily, with the result that it takes effort (a.k.a. energy) to keep the moving surface moving. Frictional drag thus occurs when you have a stationary object and a moving one. The loss of energy in the tidal situation is usually described as being due to "friction", but this can easily lead people to think that it happens because either the entire ocean or just that part constituting the bulges is stationary and the Earth is moving relative to it. This is clearly not the case, as this situation would result in vast tidal waves washing over the Earth's surface. The oceans as a whole are in fact moving at exactly the same speed as the Earth (as is, rather more obviously, the solid body of the Earth!). It's just that, locally, the surface of both the Earth and the ocean upon it is continually being deformed into bulges: this deformation loses energy due to viscous drag.
Tidal lag
There is another rather more subtle and harder to understand consequence of viscous drag and that is tidal lag. This is the phenomenon by which the tidal bulges do not sit exactly under the Moon, but somewhat in advance of it. It is called "lag" because it causes high tide to lag behind the passage of the Full Moon across the sky of an observer. The usual explanation of tidal lag is that friction between the Earth and the tidal bulge drags the bulge forward somewhat in the direction of rotation of the Earth, thus placing it in advance of the Moon. However, as we saw above, the concept of "tidal friction" is a bit of a tricky one so we must again consider the physics of the situation in order to understand how tidal lag really comes about.
I have again put the details on an extra page, so those who are keen for a little more physics should click here. The rest will just have to accept the result that the energy dissipated through viscous drag will modify the response of the oceans to the driving stimulus of the tide-generating force so that instead of the bulges being either exactly under the Moon ("direct tides") or exactly 90deg away from it ("inverted tides"), they will sit at a little more than 0deg or a little less than 90deg. The phrase "the friction drags the bulge forward" is therefore a rather too simplistic description of what is really happening, as it would lead one to assume that the bulge would be dragged forward in all cases. It is only when the situation is analysed in terms of the change in the phase lag of a forced harmonic wave that the true behaviour emerges, and we see that while a bulge originally in line with the Moon will indeed move forward a little, in accordance with expectations, one originally at 90deg to the Moon will actually move backwards - not at all as expected.
This second and unexpected effect has a relevance (albeit a rather theoretical one!) within the Dynamic Theory of the tides. It means that whether a tidal system is direct or inverted, the effect of dissipation is to move the bulges such that there is a net force on the Moon in the direction of its motion. In the case of direct tides, the bulge originally under the Moon will move a little forward of the Moon, thus producing the force (the other bulge, being very much further away, has little effect). In the case of inverted tides, the bulge originally 90deg forward of the Moon moves back a little and that originally at 90deg behind the Moon moves to more than 90deg behind. The first bulge is thus slightly nearer to the Moon than the second and so the net force is again along the Moon's direction of motion (though very much smaller than in the direct tides case). As we shall see, this result is very important for the consideration of the recession of the Moon.
The height of the tides
Before I move on to the next stage of tidal theory development, this is perhaps a good point at which to consider the height of the tides rather than just how they are produced. I had to do a considerable amount of research to find out how to calculate these values, so I've put the results on a separate page. Click here to read all about it. Alternatively, if you just want the answer, then it's that the maximum height of a deep-ocean tide is 94cm (37 inches), attained when the Moon is at its nearest to the Earth, the Earth is at its nearest to the Sun, and the Moon is in a direct line between the Earth and the Sun (the so-called Perigean Spring Tide). The corresponding tide in the solid body of the Earth is 66cm (26 inches).
The influence of the Earth's landmasses
Thus far, I have only considered the case of a smooth-surfaced Earth which is completely covered by water. The assumption of a smooth surface is very accurate on a global scale: the Marianas Trench (10,911m below mean sea-level) is only 0.085% of the Earth's diameter and would appear as a defect just 49microns deep, or half the width of a human hair, on the surface of a billiard ball. However, and vitally for our discussion, the surface variations are of the same order of magnitude as the depth of the water layer. This means that as the oceans move to and fro across the Earth's surface as a result of tidal currents there will be a "true" frictional interaction between them and the irregularities in the surface, leading to an additional source of energy loss. More importantly though, the irregularities that break the surface of the oceans to appear as land areas will have a major impact on the tides, as of course the tides must flow round the continents rather than go straight over them. Solid landmasses will bring tidal currents to a dead stop and channels between the continents will accelerate and divert the currents, resulting in a pretty chaotic global picture. Even locally, the shape of the coastline upon which the tides impinge has a major effect. Tidal friction is greatest in shallow seas, which also tend to slow up water movements thus delaying the times of high and low water, and estuaries can amplify the tidal range due to resonance. This is the phenomenon by which the variations of water level from the previous tide which have been reflected back by the closed end of the estuary meet those produced by the incoming tide in exactly the correct time relation for the instants of high and lower water to coincide. They thus reinforce each other, producing very large resultant tides: well-known examples would be the Bristol Channel in the UK and the Bay of Fundy in Canada. Conversely, if high water meets low water they cancel out, giving a very small resultant. All in all then, not very like the original assumption.
The global pattern is even more complex, but to show it requires a map of the tidal patterns across the Earth's surface, which only began to become available in the mid-19th Century. Detailed information and truly global coverage had to wait until the advent of deep-ocean survey ships and, more recently, Earth-observation satellites. Earlier attempts to correlate predictions with actuality gave mixed results due to the sparseness of the data. Also, because the tides at specific locations were known to be heavily affected by local conditions (as mentioned above), tide tables were constructed for individual ports by analysing how the actual tides varied and fitting the parameters of a general model to this analysis, rather than attempting to apply a global model. When the actual deep-ocean tides were plotted the result was rather different from expectations!
The most dramatic finding was that the "tidal bulges travelling round the Earth" concept was false - there are in fact no oceanic tidal bulges as such. This meant that the general idea that there would be inverted and direct tides caused by phase differences between the free and forced waves had no meaning. It also put something of a serious question mark against the proposed mechanism by which the Earth-Moon distance is increasing. Last but not least, it meant that the pretty diagrams of tidal bulges and the like in textbooks (and websites and TV programmes!) were simply works of artistic fiction. Bit of a shame really - all that work for nothing.
Well, not quite. The good news is that every part of the analyses I have gone to such lengths to explain is totally correct, up to the point where we try to apply the conclusions to the actual Earth rather than an idealised Earth. The confounding factor when we try to do so is the presence of land. This doesn't just modify the oceanic tides somewhat but totally reconstructs them. Were there no land, there would indeed be travelling tidal bulges and bands of inverted & direct tides. Tidal bulges are exactly what we see in the case of the solid tides raised in the body of the Earth. Rather obviously, solid tides are not obstructed by having land in the way, as they are waves in the land in the first place! The bulges are thus free to propagate round the Earth without hindrance. However, the solid tides are always direct because, as we saw above, their propagation speed is great enough to keep up with the tide-generating force. We do have to have a re-think in the case of oceanic tides though.
The actual tidal picture
So what do the real oceanic tides look like? The answer to this question depends on the fact that, with the exception of the Southern Ocean and the far Arctic, there is no place on the Earth's surface where there is water in a continuous band round the entire circumference. This is the fundamental reason why the "travelling bulge" picture does not hold in practice. The oceans instead tend to be in the form of enormous basins - three of similar size (North Atlantic, South Atlantic and Indian) and one much bigger (Pacific). The South Atlantic and Indian basins are open to the Southern Ocean, as is the eastern Pacific; the western Pacific is rather more isolated because of the S.E.Asian island chain & Australia, and the North Atlantic has no direct connection with the Southern Ocean at all.
There's an animation coming up shortly but I shall start a textual description by considering a tidal bulge sitting in the south-eastern part of the South Atlantic. The water will want to flow to the north in order to equalise the levels but the southern hemisphere Coriolis forces make it veer off to the left, which in this case is west: it will thus follow the curve of west-African coastline, cross over to South America and head south. The leftwards Coriolis force is now to the east so it curves down the eastern coastline of South America. If there is another tidal bulge arriving at the same time as the flow reaches the lower part of South America the two will reinforce each other, sustaining the circular flow pattern as a standing wave. For this to work, the cycle time of the standing wave round the northern part of the South Atlantic must be close to the rate at which tidal bulges arrive at the southern part. A reasonable distance to take for the width of the South Atlantic might be 3500mls. We know that a deep-ocean wave moves at about 450mph, so it would take it about 12.2hrs to complete the half-circle, which is pretty close to the [theoretical!] time between successive tidal bulges. While approximate, this calculation shows that a self-sustaining circular tidal pattern here is quite likely.
Moving up to the North Atlantic, as it is not connected to the Southern Ocean its tidal forcing comes indirectly, via the South Atlantic. As the high tide crosses between Africa and South America some of it strikes the upper part of Brazil and initially deflects north rather than curving to the south. We are now in the northern hemisphere though, so the Coriolis force acts to swing it to the right. It thus moves back to the east, passing to the north of the "nose" of Africa before sweeping past the Iberian peninsula and up into Europe. At this point the Coriolis force would tend to push it further east so a certain amount rushes out past the UK into the Arctic Ocean: this accounts for the unusually high tidal range experienced by the UK. Most of the flow is constrained by the shape of the North Atlantic basin to continue round anti-clockwise though and so heads for Canada, where a further proportion diverts to the north of the American sub-continent. The remaining tide then flows down the Atlantic seaboard of the USA and through the Caribbean islands to join the flow coming up from the South Atlantic. The high tide thus completes an entire circuit, and as the North Atlantic is similar in size to the South this will take about 24hrs. There should thus be two high tides circulating at once, the first having got to the vicinity of Greenland as the next starts off in the south: this is indeed born out by the facts.
The circulation in the Indian Ocean basin is similar to that in the South Atlantic, but actually consists of two contra-rotating circulations rather than just one. There is an anti-clockwise motion centred on the island of Madagascar to the west and an inter-linked clockwise rotation to the east. The latter seems to be caused by interactions with the flow emanating in the Pacific passing to the south of Australia and with the westward-moving circulation in the Southern Ocean.
The Pacific basin is the most complex to analyse, due to its greater size. The southern section has similarities to the Indian Ocean, with an anti-clockwise circulation round New Zealand linked to a clockwise circulation in the area of Easter Island to the east. The north-west section is then driven by the north-going flow at the meeting point of the contra-flows in the south. This generates a clockwise circulation down the southern part of the USA and the western seaboard of South America (initially assisted by the Coriolis force) which joins the Southern Ocean "bulge" at Cape Horn, and an anti-clockwise circulation past the northern USA and Canada. This is moved further west by the anti-clockwise circuit below it so eventually goes past the Bering Strait, far-eastern Russia and Japan before merging with the eastern Indian Ocean circulation in the S.E.Asian islands area. This much longer route takes more time to traverse than the other circulations of course, and has no driving force other than the flow from the Bering Strait. The result is that the tides in the north-western Pacific tend to be spaced by 24hrs not 12hrs. A similar interaction between the circulation patterns in the Pacific and the tidal bulges passing along the Southern Ocean produces the unexpected result that the tides along the Antarctic coast are also diurnal rather than semi-diurnal: rather ironic that the only body of water that could have freely-circulating 12hr "bulges" does not, in fact, do so!
The above is a rather approximate summary of a very complex situation of course, but serves to illustrate the basic processes which are at work. The various circulations described can be seen in the next animation, the original version of which was produced by the Scientific Visualisation Studio of the NASA Goddard Space Flight Center from data provided by the Topex/Poseidon Earth-resources survey satellite. I have reduced its length somewhat, so it now shows just one complete "day's-worth" of tides over and over again. Red represents high water, blue low water.
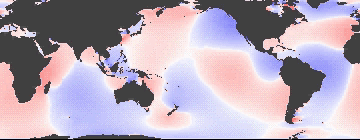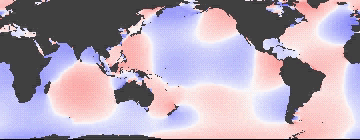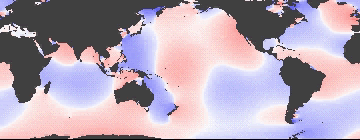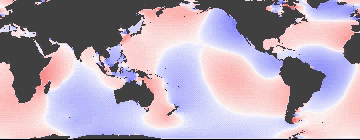
As we can see, the simplistic result predicted by the "water-covered sphere" model is clearly somewhat far from the truth. Instead of two distinct high-water areas, we have a complex pattern of tides over the entire ocean surface. Note particularly that the red patches go past Japan and the Antarctic at half the speed at which they go along the coastlines of South America and the USA, and are twice as long: this bears out the statement made above that these areas have 24hr tide cycles. Note also the two patches of red circulating in the North Atlantic, giving this basin its 12hr cycles. Students of obscure linguistics would no doubt wish to know that the centres around which the various circulations rotate are called amphidromic points, from the Greek for "running both ways": a good one to throw in when the next dinner party conversation begins to drag?
Tidal dissipation and the distance of the Moon
The lack of oceanic tidal bulges does however, as mentioned above, raise awkward questions about the usual mechanism put forward by which the tides cause not only the rotation rate of the Earth to slow but also the distance to the Moon to increase.
The rotation rate slows because of the energy dissipated in viscous drag and in frictional effects as the tides move across the ocean floor and along coastlines. This energy loss heats up the oceans ever so slightly but can only come from the rotational energy of the Earth, which therefore decreases leading to a slowing of the rotation rate. This mechanism does not depend on any particular tidal pattern and so will operate whether there are distinct bulges or not.
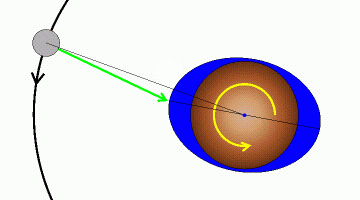The increase in the Earth-Moon distance is normally explained via the agency of the tidal bulges which, as shown by this diagram, are pulled forward of the Moon by the frictional drag between the oceans and the Earth's surface as it rotates in the direction of the yellow arrow (I will retain this terminology even though, as we have seen, it is not strictly accurate). The gravitational attraction of the nearer bulge for the Moon, shown by the green arrow, is therefore in front of the centre-to-centre line and so would be in such a direction as to have a component along the Moon's orbit. This would speed it up, leading to an increase in the size of its orbit [If you are not clear why this should be so, my article on Orbital Dynamics explains the physics of this situation]. However, if there are no oceanic tidal bulges, how can all this happen?
One apparently obvious candidate is the solid tides. We saw above that they are not disturbed by the Earth's landmasses and so have the classical "double-bulge" profile. This profile would be dragged forward somewhat by the Earth's rotation, as the body of the Earth is not totally rigid, and would thus speed up the Moon in the manner described above - exactly as per the diagram, in fact. The most modern observations show that the bulges are moved forward by only 0.2deg though, with the result that, as I show in my article 'The Recession of the Moon', the amount of speed-up that could be provided by the solid tides is entirely insufficient to account for the observed increase in lunar distance.
An alternative explanation depends on the concept of angular momentum. This expresses the tendency of a spinning object to continue spinning, in the same way that linear momentum (often called "inertia") is a measure of a moving object's tendency to keep moving in a straight line. As with many physical quantities, angular momentum is conserved i.e. it can be transferred from one body to another but cannot just "disappear". In the case of the Earth-Moon system, if the spin angular momentum of the Earth decreases, some other angular momentum must increase. Because the spin rate and orbit rate of the Moon are locked together (as the Moon is in a synchronous orbit), they together constitute the only candidate for change. Momentum is defined as mass times speed and as the mass of the Moon clearly cannot change its speed must do so. A decrease in the spin speed of the Earth thus causes an increase in the orbit speed of the Moon (together with a small increase in its spin rate to ensure synchrony is maintained). This is all very well, but any such change requires an agent - it can't just "happen". We are thus back to the same situation - what is the agency by which the Moon's orbit speed is increased? We must return to the oceanic tides for an answer.
Are there tidal bulges after all?
In the next animation the green and red lines are 180deg apart and represent the current longitude of the two "arms" of the tide-generating force: they would also represent the tidal bulges in the "water-covered sphere" model. I have placed the green line over the high tide to the east of Africa, and it can be seen that the red one aligns pretty well with the major area of high water in the central Pacific. If you click or tap on the animation to start it going, the lines will advance to the west at 15deg per frame: this corresponds to 1hr of time. [In reality, of course, it is the Earth that is advancing to the east as it rotates, but moving the lines the other way is exactly equivalent and makes the situation much clearer]
It is noticeable that although there are many areas of high water, almost all of them have their highest level (i.e. deepest red colour) at the time when a line is passing over them - most clearly for those areas near the equator. This shows us that the tidal circulations are indeed being maintained by the periodic effect of the tide-generating force, the maximum point of which gives them an extra "kick" each time it passes over by creating a particularly high water level.
In terms of producing an effect on the Moon's orbit, one could say that these highest highs are actually "mini-bulges"! In fact, they compare quite well in size to "theoretical bulges". Another of the NASA Goddard TOPEX maps shows that the typical height of a "mini-bulge" is 60-70cm while, as stated above, the maximum theoretical height is 94cm. It is thus clear that, even with the intermittent nature of the influence exerted by the real tides (because the tide-generating force clearly cannot raise bulges when it is over a continental landmass) the mini-bulges would have a considerable effect as long as there was a lag between them and the orbital position of the Moon. In this respect a mini-bulge is no different from a theoretical bulge: they are both formed from non-rigid water and so both will be affected by a lag. In fact, the most recent measurements show that the effective lag is 2.9deg. I say "effective" because of course in addition to the larger mini-bulge currently being "kicked" by the Moon at any given time, some of the other mini-bulges will be pulling the Moon back and others will be pulling it forward. The 2.9deg value thus represents the net result of many individual influences rather than the actual lag value of a single large bulge - it is usually portrayed as the latter in simplified diagrams however.
The very large lag value is almost entirely due to the amount of energy dissipated by frictional effects in the deep oceans, shallow seas and continental coastlines. This is far greater than that dissipated by viscous drag as the bulges pass through the oceans, as the viscosity of water is quite low (even taking into account the turbulent nature of oceanic viscous dissipation). The oceanic lag value should be compared to that of the tides in the body of the Earth of just 0.2deg, which is entirely due to (laminar) viscous drag. Coupled with the fact that water is more deformable than rock (hence the difference in height of oceanic and solid tides we have seen previously) this much greater lag means that, despite their irregular form, the oceanic tides are in fact more than 20 times as effective as the solid tides in affecting the Moon's orbit.
The above discussion has therefore lead us round in almost a complete circle. From the initial judgement that the complex system of tidal rotations present in the actual oceans could not be sufficiently structured to exert a coherent influence on the Moon, we now see that more detailed analysis shows there is in fact a 12-hourly pattern of "mini-bulges" which are of sufficient magnitude to cause a significant effect. This provides us with our mechanism to transfer angular momentum from the Earth to the Moon and thus cause its orbit radius to increase. As ever with anything to do with the tides, however, a full explanation of how this actually happens is not straightforward. Sufficiently complex, in fact, that it is the subject of a whole article to itself! To get the full story, read "The Recession of the Moon" when you get back to the Index.
