As I said on the previous page, although not exactly rare, lunar occultations are relatively unusual. Here I discuss why this is so, and give some idea of what I mean by "relatively unusual".
There are two basic reasons why occultations are uncommon. Firstly, for an occultation to occur at all the "celestial geometry" clearly has to be correct in order to place Earth, Moon and planet in the right relative positions in the sky. Achieving this is not entirely straightforward. Secondly, even when the alignment is correct, because the Moon is very close to the Earth (astronomically speaking!) and thus appears to be in a slightly different position in the sky at different points on the Earth's surface, the precise line of sight is only achieved over a small area - this is similar to the situation with total solar eclipses. And then of course if the event takes place when the sky is bright it may not be observable anyway!
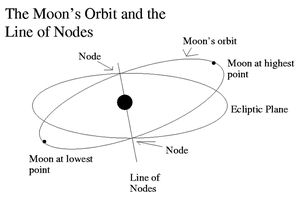
In terms of celestial geometry, the main problem is that the Earth, Moon & planets do not lie in the same plane - the orbit of the Moon is tilted at 5.14 degrees relative to that of the Earth, for example, and the same is true of the planets but to a lesser extent - 3.40 deg for Venus, 1.85 deg for Mars, 1.30 deg for Jupiter and 2.48 deg for Saturn. While the large apparent size of the Moon in the sky will largely accomodate the relatively small out-of-plane offset of the planet being occulted, its own orbital tilt is quite sufficient to prevent an occultation from happening at all. In order to ensure that one can happen, the Moon needs to be sitting very close to the plane of the Earth's orbit - called the ecliptic plane. Clearly, it must also be on its own orbital plane. Basic solid geometry tells us that there are two points where an orbit in one plane passes through another plane which the first is intersecting - these points are called nodes, and the straight line joining them is the line of nodes. It is only when the Moon is close to a node that an occultation can happen. While not to scale in terms of the angle between the Moon's orbit and the ecliptic plane, the diagram below shows the general principle well.
 |
If the Moon is close to its highest or lowest point then even if a planet were to be in that direction as seen from the Earth the Moon could not possibly occult it, as the planet would be sitting close to the ecliptic plane but the line of sight from the Earth through the Moon would pass well above or below it. It is only when the line of sight passes almost exactly along the ecliptic plane that an occultation can occur, which requires the Moon to be close to one of its orbital nodes. |
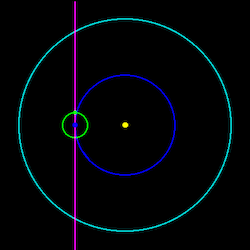 |
The above condition does carry with it another potential problem though. The Moon orbiting round the Earth constitutes a sort of enormous gyroscope, and gyroscopes don't like being disturbed. Accordingly, the pointing direction of the line of nodes tries to remain fixed relative to the distant stars as the Earth/Moon system orbits the Sun, rather than being carried round with the Earth in a sort of "lighthouse" fashion. As a consequence, the line of sight along the line of nodes can only intersect a small part of the orbit of the outer planets (two arcs each the width of the Earth's orbit, in fact), seriously limiting the opportunities for an occultation. The diagram on the left illustrates this. The light blue circle represents the orbit of an outer planet, the dark blue circle that of the Earth, and the green circle that of the Moon. The purple line shows the line of sight along the line of nodes. Click or tap on the diagram to set the Earth-Moon system in motion. |
As you can see, it is just those parts of the orbit of the outer planet which get coloured red which can be intersected by the line of sight, and so the planet can only ever be occulted by the Moon when it is on those arcs - in total, about a third of its orbit in the case of the hypothetical outer planet in this diagram. And don't forget that while the diagram slightly over-states the distance of the nearest outer planet (Mars), it greatly under-states the distance of the farthest. Jupiter is 5.2 times as far from the Sun as the Earth and Saturn is 9.6 times and so the total "occultation zone" for these planets will actually be much smaller than shown by the diagram - just 7% of its orbit in the case of Saturn.
| The inner planets (Venus and Mercury) can, of course, also be occulted as the line of sight extends inwards towards the Sun as well as outwards. The situation is slightly different though as, because the orbit of the Earth is larger than that of the inner planets, the line of sight can intersect their entire orbit during the course of a year. However, much of the time it will actually miss doing so as it will lie outside the orbit radius, meaning that no actual occultation will be possible during these periods. The diagram on the right illustrates this. As before, the dark blue circle represents the orbit of the Earth, and the green circle that of the Moon, while the grey circle represents the orbit of an inner planet. Once again, the purple line shows the line of sight along the line of nodes. Click or tap on the diagram to set the Earth-Moon system in motion. | 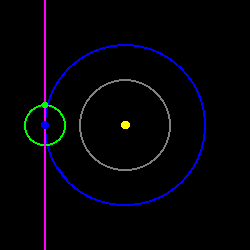 |
The final frame of this animation is very similar to that for the outer planets but this time the red arcs show that part of the Earth's orbit where an occultation is possible rather than the relevant part of the outer planet's orbit. The conclusion is the same though - there will be large periods during any year when an occultation cannot happen.
As a consequence of the above issues, lunar occultations of both inner and outer planets should be very unusual. Fortunately, things are not quite as bad as portrayed because, due to gravitational disturbance of the Moon's orbit by both the Sun and the Earth, the pointing direction of the line of nodes does actually slowly turn clockwise (one rotation taking 18.6 years) in a process called precession - which also happens to "small-scale" gyroscopes. This means that instead of the direction of the line of sight along the line of nodes being exactly the same year on year, it will steadily move to the right by almost 20 degrees per year. Combine this with the Earth's orbital motion and, over time, each part of the orbits of the outer planets can be "in the firing line" for a potential occultation. It does still require a planet to be actually there of course, but the situation is much better than for the "no precession" option. The next diagram shows this situation. Again, click or tap on the diagram to set the Earth-Moon system in motion.
 |
As the line of sight slowly turns because of precession, not only are the arcs of intersection greater than before but they also begin to include parts of the orbit of the outer planet which could not be reached in the no precession case. The actual situation is somewhat complicated because as the line of sight is turning clockwise the Earth's orbit takes it anti-clockwise, but I think it is clear that, given time, all parts of the outer orbit will eventually be intersected. |
| The situation for the inner planets is rather similar, with the slow rotation of the line of nodes eventually allowing occultations to happen at all points on the Earth's orbit. Once again, click or tap on the diagram to see this process in action. In all cases though, predicting exactly when occultations will occur is not a straightforward process as the calculation involves the precession period & direction, the motion of the Earth & Moon, the motion of potentially occultable planets and their distance away from Earth, and the starting positions of Earth, Moon and planets at the beginning of the calculation. |  |
As I said right at the beginning of this page, even though the circumstances for an occultation are all established it still might not be visible from a given location because, although the apparent size of the Moon is large, it is also quite close to the Earth, astronomically speaking, and so its position in the sky differs depending on the exact position on Earth of the observer - by as much as 2 degrees (four times the Moon's diameter) from one side of the Earth to the other, in fact. And of course to be visible at all (or at least easily so) the event must really happen during darkness. These factors further complicate the calculation of the circumstances for occultations. I have therefore not attempted to do this, my dates being derived from an essentially brute-force search using the astronomical calculation program Solex. Any conclusions which can be drawn must therefore be based on the discovered dates of occultations rather than those derived from theory.
My search using Solex generated dates for occultations from 2007 to 2040. I have extracted from the list the intervals between successive occultations for Venus, Mars, Jupiter & Saturn which would be, in theory, visible from my location (North Suffolk). I say "in theory" because some of these events would be either in daylight or very low down (or both!). However, this doesn't change the fact that an occultation did/will occur and so I think it is reasonable to include these events. The results, in years except where stated, are as follows:-
Venus - 1.46, 7.35, 4.20, 3.39, 1.86, 0.99, 1.69, 3.30, 0.33. 6.55
Mars - 138 days, 5.00, 9.58, 2.03, 14.96, 108 days
Jupiter - 4.21, 3.16, 3.47, 7.68, 3.84, 2.94, 27 days
Saturn - 81 days, 7.65, 9.82, 136 days, 6.30, 5.63, 54 days, 81 days, 27 days, 4.05
So - what can we deduce from that lot? At first glance, not much! As far as I can tell, the intervals in years for each planet are essentially random, with no obvious connection to orbital periods or suchlike. This does tend to confirm the complex nature of the interactions between the various factors outlined above and the difficulty of predicting occultations by calculation. However, the intervals in days tell a more interesting story as they are all integer multiples of the period between successive passages through a given lunar orbital node - the draconic period - of 27.2 days. It would seem, therefore, that on some occasions when the geometric line-up is correctly established it can persist for quite some time - for at least 5 nodal months on these figures. In fact, a table of occultations visible globally available on the Internet (here) shows there can be as many as 12 successive occultations of Jupiter and Saturn, each one draconic month apart, and 3 for both Mars and Venus. Given that the Earth and the target planet are both moving, and the line of sight is also changing with time, an exact line-up clearly cannot be maintained for such a long period, so the possibility of successive events is really down to the large apparent size of the Moon in our skies, meaning that the alignment need not be perfect for an occultation still to be seen. The difference between the number of repeats involving Mars & Venus and Jupiter & Saturn is caused by the slower motion and greater distance of the latter pair, which enable a line-up to be maintained for a longer time.
But, I hear you say, how often do occultations actually occur? Well, based on the list of intervals above, in the period in question (2007 to 2040) the answer for my location is Venus 11 times, Mars 7 times, Jupiter 8 times and Saturn 11 times. The count of those actually fully visible is much lower though - Venus 2 (1st Dec. 2008 & 10th Jan. 2032), Mars 1 (8th Dec. 2022), Jupiter 2 (15th July 2012 & 21st Nov. 2034) and Saturn 4 (2nd Mar. 2007, 21st Aug. 2024, 4th Jan. 2025 & 9th Dec. 2036). However, because Venus is so bright it can often be seen in the daytime if you know where to look so we perhaps only need to exclude events low in the sky (say less than about 5 degrees). This brings the total for Venus up to 8 - including the one I actually observed on 9th Nov. 2023.
Expanding the search to the whole Earth over the period 1990 to 2050 (using the online tabulation mentioned above), the total numbers of occultations of the four planets are not greatly dissimilar (95, 84, 107, 116 respectively) - I assume the somewhat higher numbers for Jupiter and Saturn are because of their greater distance (which affects the geometry) and slower motion (which means they tend to stay "in line" for longer). The "per year" profiles were very different though, with Venus & Mars both having between 0 and 4 occultations per year in a fairly random fashion, Jupiter usually having between 0 and 2 but with occasional peaks of 6 to 10, and Saturn showing a very "peaky" distribution where the usual number was 0 but with surges of 9 to 12 at quasi-periodic intervals (7, 4, 6, 7, 5, 5, 7, 5, 5, 7 years). Click on the planet names (just above) to see the profile for each.
In the case of the occultation intervals for Saturn, I was interested to note that sets of these numbers (such as 7, 5, 5, 7, 5) add up to 29 years, the orbital period of Saturn, so I made a longer investigation to see whether the pattern actually repeated. Going back as far as 1962 I found it sort of did, the longer sequence being 5, 7, 6, 4, 6, 7, 4, 6, 7, 5, 5, 7, 5, 5, 7. As can be seen, the last five intervals are almost the same as the first five, the middle five are a re-arrangement of almost the same numbers, and the totals are 28, 29, 29. Indeed, if you add up any consecutive five intervals the totals only range between 27 and 30, with an average value of 28.45 years, which is very close to the orbital period of Saturn (29.45 years). But is that just a coincidence?
This finding prompted me to look again at the profile for Jupiter, and I noticed the near repetition of a pattern of higher numbers of occultations which will happen in 2026/2027, 2034, 2037/8, 2041 & 2048 at intervals of 7.5, 3.5, 3.5 & 7 years, which also occured in 1990, 1998, 2001/2, 2005 & 2012. Note that a forward slash ("/") indicates that these years had equally high (but not very high) numbers of occultations. Accordingly, I have used the mid-point between them when calculating intervals. Admittedly, the "peak" in 1990 was only a small one (3) and there should have been occultations in 1991 but there were none, and the numbers of occultations are different in the two patterns, but some variation in this complex process is to be expected. I thus felt that the repetition pattern was confirmed, but to check the full sequence of intervals I went back to 1976, which should have been the previous peak before 1990 - and indeed it was. I also went forward from 2048 and found the next peak in 2063. Taking into account the 14.5 year interval between the two sequences noted above, the full pattern of intervals was thus 14, 8, 3.5, 3.5, 7, 14.5, 7.5, 3.5, 3.5, 7, 15. Depending on whether the large gap is taken as the start of a sequence or the end, the repetition period can be calculated as either 36 or 36.5 years, to give an average of 36.25 years which is very close to three times the orbital period of Jupiter (35.58 years) - surely not another coincidence?
Finding a repetition period which seems to have a relationship to an orbital period is one thing but determining the reason this should be so is quite another! I thus played around with the numbers a bit and came up with the following.
Taking the case of Saturn first, let us assume that at a given moment it is at the "12 o'clock" position on its orbit (relative to the diagrams above), with the Earth at the same position on its orbit and the line of nodes pointing directly at Saturn. After one year, the Earth will be back at 12 o'clock but Saturn (travelling anti-clockwise) will be approaching the "half past 11 o'clock" position, having moved a fraction more than 1/30th of its 29.45 year orbit. To restore the "same position on orbit" situation the Earth will thus have to travel on for about another fortnight. The time between these successive line-ups is known as the Synodic Period, and is actually 1.035 years for Saturn. Given that Saturn moves round a little less than "half an hour" for each synodic period (12.7 degrees, in fact), it takes 29 synodic periods for it to get back to a line-up very close to 12 o'clock, which it does in 30 years almost exactly. As this is slightly more than its orbital period the line-up is in fact just to the left of 12 o'clock, but the offset is very small.
So, we now know that both the Earth and Saturn will return to their original positions after 29 synodic periods (30 years), but this will not result in the line of nodes also being re-aligned as its rotation period is 18.61 years. To return everything to the original position we need to find what number of synodic periods is equal to not only a whole number of years (to ensure that the Earth, and therefore Saturn, is back at 12 o'clock) but also to an integer multiple of the nodal precession period (or an integer plus one-half, as the line of sight projects in both directions). It turns out that there is no number which satisfies both criteria simultaneously, but the nearest are 27 and 28 periods. The first is equal to 27.949 years and 1.502 times the precession period, the second being 28.984 years and 1.558 times the period. Note that the average repeat interval of the sequence of occultations as determined above (28.45 years) sits between these two values.
In the case of Jupiter, because it moves faster than Saturn the Earth takes more time to catch up and so its synodic period is longer - 1.092 years in fact. This means it moves round a little more than "one hour" for each synodic period (33 degrees, in fact), and so takes 11 synodic periods to get back to a line-up very close to 12 o'clock, which it does in 12 years almost exactly. As with Saturn, because this is slightly more than its orbital period the line up is again just to the left of 12 o'clock, but the offset is equally small.
We now need to carry out the same calculation for Jupiter as for Saturn - what number of synodic periods is equal to both a whole number of years and also to an integer multiple of the nodal precession period (or an integer plus one-half). Again, there is no number which satisfies both criteria simultaneously, but the nearest are 33 and 34 periods. The first is equal to 36.036 years and 1.936 times the precession period, the second being 37.128 years and 1.995 times the period. As with Saturn, the average repeat period of 36.25 years lies between these two values.
The above calculations show that, while the near correspondence of the repeat interval for the two planets to multiples of their orbital period is not exactly a coincidence, it does not tell the whole story because it is actually the synodic period which determines the timings. The near correspondence is mainly because for Jupiter and Saturn the synodic period is quite close to the orbital period. Also, because there are, in each case, two values of synodic period which can produce a close re-alignment of both the planets and the line of nodes, there will tend to be (as found) a slight variation of the repeat interval with time. However, because one of these values produces a closer re-alignment of the planets (i.e. it is nearer to a whole number of years) and the other produces a closer re-alignment of the line of nodes (i.e. it is nearer to an integer or integer plus one-half multiple of the precession period), this variation will tend to even out, thus keeping the repeat sequence stable.
These analyses do seem to convincingly show why the repeat intervals of the pattern of number of occultations per year of both Jupiter and Saturn have the value they do, which I found very pleasing. The calculations do not, however, explain why the repeat patterns should take the form that they do. Why should Saturn experience either a very large number of occultations in a year or literally none? Why is the pattern for Jupiter so irregular? The answer in both cases is very simple - I have no idea! By which I mean that I presume these characteristics must be produced by some sort of resonance between the Moon's nodal precession period and the orbital motion of the planets and the Earth so that, periodically, the amount the line of nodes has rotated is just enough to compensate for the motion of the Earth and the occulted planet, thus restoring the correct geometric line-up and permitting another sequence of occultations, but what that resonance might be I have so far been unable to determine.
Visualising the situation is of course made more difficult by the fact that the line of nodes moves clockwise while the planets orbit anti-clockwise. Also, the great difference in scale between the Earth-Moon distance and the distance to the outer planets (a factor of over 1800 for Jupiter and almost 3700 for Saturn) means that attempting to gain some insight into the problem by, for example, constructing an accurate simulation might not be helpful (or indeed practical). In the apparently simpler case of the pattern for Saturn it would just about be possible to squeeze a "to scale" simulation onto a "4K" screen (3840x2160 pixels) but the Earth-Moon distance would then be just one pixel! (and of course the heavenly bodies themselves could not be shown, as the scale size of even Saturn would be less than 1/3 of a pixel). I am therefore going to have to leave things at this point, inviting any reader with a better sense of visualisation for complex motion than I have to take it from here!