The clue to the unusual circumstances of this eclipse is the fact that the times of moonrise and sunset at my location were 8:48pm and 8:51pm respectively. These times relate to the centre of the bodies however, so given that each takes about 4 minutes to fully rise (from just visible to fully above the horizon), it would seem that at about 8:50pm the totally eclipsed Moon would be fully visible at the same time as about 75% of the Sun was still above the horizon. This apparently impossible phenomenon is called a Selenehelion (or Selenelion). Why impossible? Well, how can the Moon be fully eclipsed (i.e. totally in shadow, and thus with no light shining on it) when it and most of the Sun are visible in the sky at the same time?
The answer to this conundrum is the phenomenon of atmospheric refraction. Although light usually travels in a straight line, it only does so if the medium through which it is passing has a constant refractive index. This is a physical parameter of any medium, which expresses how much slower light travels through that medium as compared to in a vacuum (which has a notional index of 1). Any change in the index will cause a beam of light to deviate from a straight line, bending towards the medium with the higher index by an amount determined by the angle at which it strikes the boundary between the two media: a shallower angle produces more deviation. The effect is similar to what happens if one drives a car at an angle from a tarmac road onto sand: the greater drag of the sand as compared to the tarmac means that the front wheel which is in the sand cannot travel as fast as the one on the road, i.e. sand has a higher "refractive index" than tarmac, and so the car will tend to swerve towards the sand.
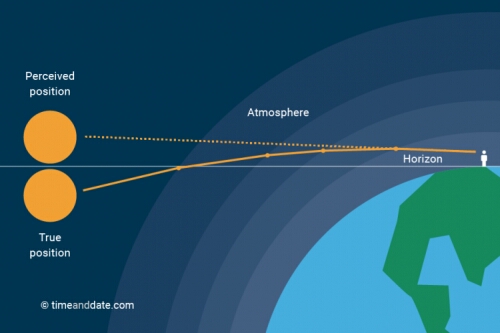
The refractive index of a gaseous medium such as the atmosphere is greater the more dense it is, and of course the density of the atmosphere increases the closer one gets to the Earth's surface. Light from a celestial object passing through the atmosphere will thus encounter an increasing refractive index as it travels from outer space towards the Earth's surface, causing it to bend slightly towards the surface. The deviation will be relatively slight, as the change in index with change in density is not great, but it will be at its largest when the light approaches at a shallow angle (so it passes through a greater depth of atmosphere). For a beam of light approaching from the horizon i.e. at a tangent to the Earth's surface, the deviation will actually be about 34 arc-minutes (just over half a degree). While not great in absolute terms, this value is highly significant as it is greater than the apparent diameters of both the Sun and the Moon - which might lead you to deduce where this argument is leading!
If one of these bodies is lying just below the horizon of an observer on the Earth's surface, there will be no direct line of sight between it and the observer, meaning that it should not be visible. However, because of atmospheric refraction, light reflected from (or produced by) the body travelling in the general direction of the observer will be bent downwards, i.e. towards the observer, enabling it to be seen. As the observer believes that light always travels in straight lines, he or she will perceive the body as lying back along the direction the light was travelling when it finally entered their eyes. Because of the refraction, this will be about 34 arc-min higher than the true source of the light, giving the impression that the body is fully above the horizon. The image below shows all this diagramatically:-

The conclusion is now fairly obvious - although the Sun and the eclipsed Moon appeared to be in the sky simultaneously, in fact they were both actually below the horizon. It is only the effect of refraction in "lifting them up" which made them both appear to be above the horizon. Numerically, the situation was as follows:-
Although sunset time was given as 8:51pm, the true instant when the last sliver of the Sun would have disappeared had there been no refraction was actually 8:49:24. At this moment, the upper edge of the (eclipsed) Moon was in fact still 11.66 arc-min below the horizon. Visually though, the Sun would have appeared to be just fully above the horizon and the Moon would have appeared to be about 3/4 risen. The Moon would truly be just rising at 8:50:57, at which time the Sun was 11.94 arc-min below the horizon. However, the observer would have seen them well above the horizon and only about 1/3 set respectively. So, although there was in truth no instant when the Sun and eclipsed Moon were actually in the sky together, visually this would have been the case for a number of minutes. The limiting cases are the time the Moon would have appeared to start to rise (8:46:26) and the time the Sun would appear to have fully set (8:53:50) - a window of 7 minutes 24 seconds! They could not, on this occasion, have both been seen fully above the horizon however - the optimum moment was at 8:50:02 when each would have appeared to be just over 92% above the horizon. Both being seen fully above the horizon is possible though, but requires the Moon to enter eclipse not so long before it rises.
The animations below show the Selenehelion "as seen" and "in truth" (i.e. without refraction), at 1 minute intervals from 8:46:30 to 8:53:30. Click or tap once to start the "as seen" animation, again to switch to the initial "in truth" view, then again to start the second animation.

So - maybe seeing is not believing, after all!
But wait a minute! (I hear you say). If refraction can bend the Sun's light sufficiently to allow an observer to see it even though it is actually below the visible horizon, surely the same principle would apply for an observer on the Moon? Would not the Sun's light be refracted round the Earth and illuminate the Moon, even though it was in "geometric eclipse"? Answer - Yes! This is why the Moon is usually somewhat visible during a total lunar eclipse even though it has no direct illumination. For a full analysis, click here.