While the ever-changing aspect of the four major moons provides considerable "artistic" interest, I decided to be a bit more scientific and see whether I could derive accurate orbital data from my observations, as I had done for the (much more easily seen) moons of Jupiter when a teenager. I thus obtained images on as many nights as I could during late 2003 and early 2004 and began work!
Having taken the images, the next step was to identify each individual moon (using an astronomy program) and then plot its position on an orbit diagram. This is clearly much easier if all images are rotated to a common orientation: the best one to choose is with Saturn "level", as then meaningful measurements of the orbit can be made. After plotting, a best fit ellipse is drawn through the points using a graphics program: this is surprisingly sensitive to even slight changes in the position of the points and so if a good fit is achieved one can be sure that the orbit is accurately plotted. Also, although the apparent size of Saturn (and hence of the moon's orbits) does not change much as the Earth moves away from it (due to the planet's great distance from us), I did find that some compensation was necessary to ensure that positions taken late in the sequence would sit on the "best fit" curve. The fact that this discrepancy was easily noticeable gives further weight to the assertion that the plots are accurate to quite a high level of precision. After plotting, the major and minor axes of the ellipse can be measured. To understand what can be deduced from these, a little geometry is needed!
It is obvious (I hope!) that if a circular orbit is seen "slant on" then the larger axis of the resultant ellipse will be equal to the diameter of the original circle. Simple trigonometry will show that the smaller axis is equal to the diameter multiplied by the sine of the angle to which the orbit is tilted. Thus, if we calculate the ratio of the minor to major axis and find the angle whose sine is that number, we have the tilt of the orbit. Now Saturn's larger moons all orbit very nearly in the plane of the rings and so the tilt of the moons' orbits is also the tilt of the rings as seen from Earth, and that value can be cross-checked because it is tabulated in astronomy programs! Things are rather more complicated for a non-circular orbit, unfortunately, as an ellipse seen slant on is no longer an ellipse: however, in general there will be a slight difference between the "left-hand" half-axis and the right-hand one which will allow an estimate to be made of the eccentricity of the original ellipse.
In the case of Rhea, Dione & Tethys, it is known that their orbits are almost exactly circular. All the plots for each moon should thus sit exactly on an ellipse and each moon's diagram should give the same value for the ring-tilt. Also, if each orbit has been plotted the correct size the ratio of each major axis to the known orbital distance from Saturn should be the same. Titan's orbit is markedly eccentric, so the plots should not quite fit an exact ellipse and the semi-major axes should be slightly different: the degree of difference will depend on the exact orientation of the orbit (which I was unable to determine) but will give an apparent eccentricity sitting somewhere between zero and the true figure.
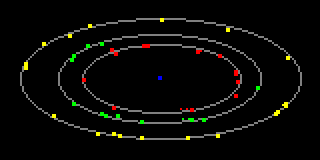
And now for the results! The picture below shows the plots of each individual observation for the three inner moons (Tethys, Dione & Rhea from the centre outwards) on the same diagram. The two small dots near the bottom of the plot for Tethys illustrate the point about rapid motion: they were taken about 1hr and 2hrs after the plot to their right.

| Moon | Minor Axis | Major Axis | Ratio | Orbital distance | Ratio |
|---|---|---|---|---|---|
| Tethys | 34 | 79 | 0.430 | 183,019mls | 2317 |
| Dione | 44 | 101 | 0.436 | 234,410mls | 2321 |
| Rhea | 60 | 140 | 0.429 | 327,354mls | 2338 |
| Average value | 0.432 | 2325 | |||
It can be seen that, remarkably, the derived figures are consistent at the 1% level: this does however tend to support the above statement that even a one pixel shift (in about 100) has a noticeable effect. The average axis ratio gives a value for the ring tilt of 25.56degs compared to the tabulated figure of 25.57 at opposition, but I will concede that this astonishing agreement does owe more than a little to luck!
In the case of Titan, the orbital plot cannot be exactly overlaid by an ellipse - see below.

In summary therefore, an extremely successful and quite surprisingly accurate project!