The mathematics of Saros series

The number of Saros series per Saros-Inex Panorama sawtooth

We know from the consideration of the aphelion/perihelion effect detailed on the main page that each plateau on gamma-value graphs is formed by eclipses whose calendar dates [corrected for precession] are centred around early January. Because the number of eclipses on each plateau is very similar, corresponding eclipses in adjacent plateaux will have almost the same calendar date. We also know that the "jump-back" in eclipse date, caused by a plateau moving into the +/-1.57 gamma zone where an eclipse is possible, is the reason for the sawtooth effect observed at the upper and lower edges of the Saros-Inex Panorama. It therefore follows that the crest of each of the "teeth" corresponds to eclipses whose calendar dates are nearly the same i.e. whose full dates are a whole number of years apart.

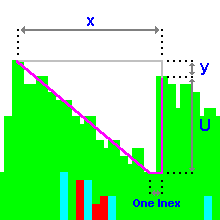Observation of the part of the Panorama I have used for most of my analyses shows that each successive sawtooth is slightly lower than the one before, so to move from the crest of one tooth to the crest of the next we must go across and then down a bit. By the definition of the way the Panorama is constructed, "across" means add Inex intervals, "down" means add Saros intervals: the date difference between two successive crests is thus xI+yS (see grey line on diagram). While there are an infinite number of ways this expression can be made up, we know that both x and y must be whole numbers and we also need the overall sum to be a whole number. I thus tabulated the sum for values of x from 10 to 30 and values of y from 1 to 4 and found there were only a small number of pairs of values that got within 6 days of giving a whole number sum. These pairs all had x equal to 18, 19 or 20 with the preferred values of y being determined by what you mean by "a year". There are two obvious candidates for this:- the "simple" calendar, or Julian, year (365.25days) and the anomalistic year (365.2596days). The simple calendar year (i.e. only taking into account the "once every 4yrs" rule for leap-years) is easier to work with in terms of calculating the number of days a Saros period is greater than 18yrs, for example, and is also close to the "normal" meaning of a year, but the use of the anomalistic year better reflects the underlying processes so is likely to be more accurate in some calculations. In the case of the simple calendar year, two value-pairs give a result which is extremely close to a whole number of (calendar) years - 19:2 and 20:4. The errors are just 28.6hrs and 60.8hrs respectively. Using the anomalistic year gives four pairs which have about the same, but much larger, error (about 5 days) - 18:1, 19:2, 19:3 & 20:4. However, the value for xI+yS averaged across these four cases is just 20.9hrs longer than a whole number of (anomalistic) years. As the same range of values holds true for both cases any analysis will not depend critically on which "year" is chosen, but the fact that the use of the anomalistic year results in four equally good answers indicates that the overall conclusion is not going to be a precise one.

There is a further complicating factor, which affects almost every aspect of Saros series, and that is what I call "Inex Triples". I have explained this concept in some considerable detail on the main Saros series page so I shan't repeat the details here, but suffice it to say that any graph showing many Saros series is actually composed of three super-imposed graphs of sub-sets of series i.e. series X is more related to series X+3, X+6 etc. than it is to the series in-between. This means that the sawtooth patterns in the Panorama are actually formed from three sets of "sawteeth", each of which is slightly out of alignment with the others - this is one of the reasons why the Panorama is rather ragged when looked at close-up. Given that of 18, 19 & 20 only 18 is divisible by 3, periodicities of 19 and 20 tend to get "smeared out" somewhat, which further reduces the precision of any numerical results. I shall thus give some general arguments in this section rather than any exact calculations.

To check that the x & y values I found really do correspond with "real life", I calculated some numbers from actual eclipses. I used Saros series from 10 to 55 for this, as this range has very distinct peaks of series having larger total numbers of eclipses. Firstly, the date difference (xI+yS) divided by the number of Inex periods in the crest-to-crest interval (the "x" value) will give the average time between new Saros series. For the "anomalistic average" date difference of 595.002yrs, this is 31.282yrs. The value can also be calculated by other means however, thus:-

The average number of eclipses per series in this range is 74.6 [from Meeus]. Thus, the average duration of a Saros series is 74.6 x 18.03 = 1345.0yrs. The long-term average number of eclipses in a year is 2.38 [from NASA and Meeus]. Thus, the average number of eclipses in one Saros interval is 2.38 x 18.03 = 42.91. So, the average interval between series is 1345.0 / 42.91 = 31.346yrs. This is very close to the calculated number so I think we can be sure we're on the right track.

This conclusion can be checked by calculating the crest-to-crest interval in a different way. Instead of going "straight across and straight down" to move from crest to crest, one can go "down the slope and up the cliff" (see purple line on diagram). Given that the overall result must be the same, a knowledge of the average time between "regular" Saros series (i.e. those not involving the jump-back) will give you the height of the "cliff", which can be compared to values taken from actual data.

Let T be the interval between regular Saros series (all but one of those comprising a sawtooth) and N be the number of Saros series in a sawtooth. The total interval from the first regular series to the last is thus (N-1) x T. Now let the average number of eclipses in the jump-back section of the sawtooth (the cliff) be U. The interval from the last regular series to the top of the sawtooth crest is then one Inex period (by definition) minus U Saros periods - minus because we are going "upwards".

So, the total interval = (N-1) x T + 28.95 - (18.03 x U). Given that the total interval must be the same as that calculated previously ( = average interval between series, which I shall call A, times no. of series), we see that A x N = (N-1) x T + 28.95 - (18.03 x U). Re-arranging the formula, we find that U=((N-1) x T + 28.95 - (A x N))/18.03

Setting A=31.282 (as calculated above) and T=44.167 (calculated from the same Saros series data as used above) we find that if N=18 then U=12.0, if N=19 then U=12.7 and if N=20 then U=13.5. In fact, the data shows that, for series around number 52, the average difference in total number of eclipses between Saros series with the high and low values (a difference which is, of course, caused by the "jump-back" that we have been calculating) is exactly 12. This is confirmed by looking at the number of eclipses making up the plateau sections of gamma-value graphs. Using data I had already gathered for series 33,34,35 and 45,46,47 I found that the average number was 11.9 but ranged up to 14.

Yet more confirmation accrues when we consider the parameter T (44.167yrs), which can be expressed as one Inex interval plus 0.844 Saros intervals. In terms of the Panorama, this means that to move from the start of one Saros series to the start of the next one must go "across 1 and down 0.844". I shall call the value 0.844 "G", as it is the gradient of the sloping section of the sawtooth. To move all the way down the slope thus takes (N-1) Inex plus (N-1) x G Saros, and to get to the next crest takes a further Inex minus the jump-back value, U. The total crest-to-crest move thus takes N Inex intervals plus (N-1) x G - U Saros intervals. For N=19 we find that the number of Saros intervals is 2.46, very close to the 19:2.5 ratio that would be needed to make xI+yS equal the "anomalistic average" date difference of 595.002yrs. It is also very close to the actual average vertical offset between the Saros-Inex Panorama sawteeth in this region: 2.4

I appreciate that the above calculations are not fully rigorous, nor independent of each other, but they do give very strong support for the assertion that, in the part of the Panorama corresponding to Saros series around 35, the periodicity of the Panorama sawtooth is the result of the super-position of cycles of 18, 19 and 20 Saros series (further convolved by the disturbing influence of the Inex Triples effect). The overall result is an average repeat interval of 19 series with an offset per sawtooth of about 2.5 Saros periods. The calculations also show that everything is determined by three parameters: the average interval between series (A), the magnitude of the jump-back (U) and the slope of the sawtooth (G). These parameters are themselves determined by factors directly governed by the Inex and Saros periods and the changes in them over time.

A, as we have already seen, is determined by the number of eclipses per year and the number of eclipses per Saros series, which is itself determined by the variation in delta-gamma caused by changes in the Moon's orbital periods. Note, however, that because the average number of eclipses per Saros series decreases with time but the average number of eclipses per year stays constant [from Meeus], A must decrease i.e. the rate at which series are "born" must increase. This is confirmed by the data - Meeus tells us that 92 new series begin in the 3000yrs from 10000BC to 7000BC, 99 from 500AD to 3500AD and 114 between 12000AD and 15000AD. A decrease in A implies a reduction in either or both of the x and y parameters in the xI+yS expression. A reduction in x means that the Panorama periodicity will decrease and a reduction in y means that the downwards step between successive crests will become smaller - it will flatten off completely if y is zero, and even turn into an upwards step if it is negative. Both these effects can be seen in the actual full Panorama, shown above. For Saros series numbered around -200 the periodicity is about 21 and the step is about +5 but for series around +600 the values are about 16 and -2 respectively. The change in sign of y means that the full Panorama is actually boat-shaped - its top edge is reasonably flat around series 340 but curves up at both "ends". I've done some work to investigate this behaviour, which you can read about by clicking the "maths page" link at the end of the Tetradia section on the main page.

Because of the way the Saros-Inex Panorama is defined, one might have expected the value of G to be exactly 1.00 i.e. that the interval between successive series would be exactly 1 Inex plus 1 Saros. The fact that it isn't is, I believe, due to the variable speed of the Moon on its rather eccentric orbit. At apogee, it will be going more slowly and so the duration of the "new Moon" Saros will be slightly lengthened. As the average "node crossing" Saros period is a little longer than the average "new Moon" Saros period, this lengthening will mean that it is more likely that the two periods will now align and thus cause an eclipse to occur i.e. the new series may start sooner than expected, resulting in an interval of just 1 Inex. Conversely, at perigee the Moon will be going more quickly and so the "new Moon" Saros interval will be reduced, resulting in a mis-alignment. This could cause a possible delay to the start of the new series and thus an interval of 1 Inex plus 2 Saros. It is even possible to have an interval of 1 Inex minus 1 Saros because, in a sequence of series separated by I+S, if one interval is increased to I+2S then an adjacent interval must become just I. If this interval is then affected by an "apogee effect" the result will be I-S. Although I and I+2S will cancel each other out, because of the possibility of I-S the overall effect of apogee/perigee variations will be to reduce the average interval somewhat from I+S, as actually found. [Note that, although theoretically possible, I+3S does not occur in practice. This is almost certainly because, as I have found in other cases of apogee/perigee effects, the magnitude of any apogee effect is much greater than that of the corresponding perigee effect. The net effect of the shifts is therefore to reduce the interval.]

U is related to the magnitude of the aphelion/perihelion effect, the average value of delta-gamma and the length of the Saros period. Delta-gamma increases with time, however, and this results in a decrease in U (as does a reduction in the magnitude of the aphelion/perihelion effect due to a reduction in the eccentricity of the Earth's orbit). Over time, therefore, the "teeth" on the edges of the Saros-Inex Panorama get steadily smaller, as can be seen on the above illustration.

Note also that the gamma values of eclipses in an "Inex series" i.e. a series formed by one row of the Panorama rather than one column, are affected by the Earth-Sun distance in exactly the same way as those in a Saros series, and for the same reason. The periodicity of the variation will be different though, due to the different number of days that an Inex differs from a whole number of anomalistic years as compared to a Saros. We have seen that the periodicity of the effect in a Saros series is about 34.30 eclipses (1/0.0292). In a similar way, it is 17.75 eclipses in the Inex series (1/0.0563). The peak variation in delta-gamma is actually larger than for a Saros series (+/-0.067 compared to +/-0.045), but because the Sun-Moon-Earth re-alignment after one Inex is more accurate than that after one Saros (currently 0.040deg error rather than 0.478deg), when averaged over a whole cycle the mean gamma shift is almost zero (currently 0.0035, compared to 0.042 for the Saros). [Note that when calculating these figures an average over three Inex series must first be performed, due to the "set of three" issues discussed earlier]. The fact that the Inex series periodicity is close to half the periodicity of the Saros-Inex Panorama, and in the same sense (i.e. in the "x-axis" direction) undoubtedly adds yet another factor to the many reasons why the Panorama periodicity is neither entirely regular nor constant.