The mathematics of Saros series

(Completely revised in March 2014)

Can we explain the variability in the Saros-Inex periodicity?

Those who have read through all my maths pages as well as the main Saros Series page will know that the decrease in the periodicity of the Saros-Inex Panorama has cropped up in two completely different contexts: the empirical formula P=565.1-1.38*T based on measurements and the fact that in the expression for the time difference between two eclipses, x*I + y*S, both x and y must decrease over time. I was intrigued to see whether I could derive a connection between the two.

I was attracted by the fact that, as mentioned in the maths page, there are several combinations x*I + y*S which give a result which is very close to a whole number of calendar years. In fact, if one accepts a discrepancy of about 0.02yrs (~8 days) there are seven pairs of "good" results for anomalistic years and three pairs and four "singles" for Julian years (where by "pair" I mean equally close results which have the same x value but y values which differ by 1). The x and y values for these combinations are [15,-6 & 15,-5], [16,-4 & 16,-3], [17,-2 & 17,-1], [18,0 & 18,1], [19,2 & 19,3], [20,4 & 20,5] and [21,6 & 21,7] for anomalistic years and [15,-6 & 15,-5], [16,-4 & 16,-3], [17,-2], [18,0], [19,2], [20,4] and [21,5 & 21,6] for Julian years.

Before I could investigate further, I needed to determine which values of x and y are associated with actual Saros series numbers. I thus analysed the entire NASA Saros-Inex Panorama to find the values for every sawtooth cycle shown there (involving Saros series from -228 to +613), and plotted them against the Saros series number of the series at the peak of each sawtooth. The plots had quite a lot of scatter (due to the irregularity of the Panorama) and so I used a three-point average to give an Excel-generated trendline formula which enabled me to derive the x & y values for a given series number.

Next, I needed to find out how the Saros series number varies with time. This is easy to determine for the series listed in the NASA data, but this only tabulates series -13 to +190 and I needed a much larger range. I attempted to find a formula by two different methods: using the information given by Meeus on the numbers of Saros series "born" in different time periods and by use of data calculated by Luca Quaglia and used by Kurt Leingartner as part of his work on "Saros Portraits" (see Mathematical Astronomy Morsels V, chapter 10) and sent to me in private communication. The main problem with the Meeus data is that it consists of just three points. I thus preferred the Quaglia/Leingartner data, which I used to tabulate the year of the first eclipse of every 50th Saros series from -400 to +400, together with values for -445 and +446 (the first and last series given in the dataset). I plotted the values, and determined the trendline using terms up to the cube (necessary because of the only slight deviation of the graph from a straight line). This was the relationship between Saros series number and date which I actually used, but as a check I did derive a formula from the Meeus data. This was very similar to the Quaglia/Leingarter relation, the only significant difference being in the cubic term. This resulted in the Meeus relation giving series numbers which were slightly greater in BC epochs and slightly smaller in AD epochs, but the variation was only about +/-1% which made no significant difference to the outcome. I am thus confident that my results are robust.

I could now use the data derived from my analysis of the Saros-Inex Panorama to give a graph of period (calculated from the values of x & y) against time (calculated from the Saros series formula). The trendline for this graph was thus a direct representation of the "empirical formula" and could be compared to the equation derived from the analysis quoted by Meeus, and also to a version I derived from the updated lunar orbit theory ELP/MPP-02. A further interesting comparison can also be made - against the formula required to produce the "whole number" periods from the x:y value-pairs quoted above.

While investigating the above relationships I always had to be very careful that I did not exceed the limits of validity of the formulae involved or rely on predictions which were clearly out of line with reality. In particular, lunar theory ELP is only specified between 4000BC and 8000AD (though, as I proved on the main page, it is in fact "accurate enough" over a considerably greater range); trendlines should involve only as many powers as are necessary to achieve a good match with the data (to avoid any potential "exponential explosion" at the limits of the data), and note must be taken of the fact that the characteristics of the Saros series underlying the investigation change quite dramatically around series 360 (also as shown on the main page). This last issue is an interesting one. The change is from most series having lower numbers of eclipses, with the occasional higher total, to the exact opposite: usually higher numbers with occasional lower totals. The reason for this is explained on the main page, so I shall not repeat it here. It does seem, however, that this change in character also affects the periodicity of the Panorama (for reasons I do not entirely understand). The "numerical" consequence of this is that in the expression x*I + y*S the value of y does not decrease as rapidly with time as would be predicted by the trendline formula - this effect can be seen in the "boat shape" of the full Panorama, which has a lesser slope in the direction of high series numbers than for low series numbers. I thus decided to limit my analysis to times up to about 60 centuries after the present (i.e. about 8000AD, corresponding to Saros series 370). In the opposite direction, I decided to go up to 100 centuries before the present (i.e. about 8000BC, corresponding to Saros series -155) as this seemed to be a good compromise between the "practical" validity of ELP and the range of data available from the Panorama.

And now the results! I have plotted the various formulae arising from my investigations on the diagram below - click to go from one plot to the next. The x-axis is centuries from the present, the y-axis is the periodicity of the Saros-Inex Panorama.

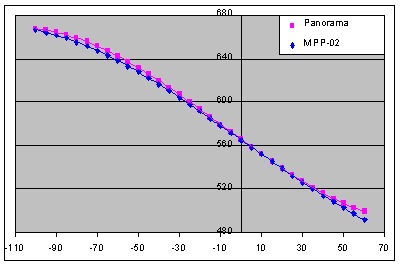The first plot shows the actual data taken from the Panorama [in pink] together with the MPP-02 version of the "empirical formula" [in blue]. It can be seen that the formula (which includes terms up to the cube) models the actual data very well. This is strong evidence that the subtle effect which causes the variation in the number of lunar tetrads is also responsible for the variation in the periodicity of the Saros-Inex Panorama. It should be noted that the shape of the plots is very similar to the central part of the baseline curve shown on the diagram between Figs.16 and 17 on the main page, indicating that the variation in the period of the Panorama is almost certainly due to the same cause: the change in eccentricity of the Earth's orbit over time.

The second plot adds in the version of the formula quoted by Meeus, which I refer to as "ELP". It can be seen that although this formula models the data well enough over a limited range (about -45 to +35 centuries) it fails badly beyond -45. This is almost certainly due to the absence of cubic (and higher) terms in the Meeus/Hughes formula, which would allow changes in eccentricity to affect the numbers.

The third plot removes the ELP line and adds in the "whole number" formula i.e. the relationship between period and date which would be required to ensure that the periods were whole numbers of [anomalistic] years. This formula is, by definition, a straight line (as each whole number period is exactly I + 2S, or 65.00 anomalistic years, away from the next) so there could not be an exact correspondence between it and the actual Panorama data. Nevertheless, the alignment is pretty good. One of the reasons it is not even better may be the existence of "Inex Triples", as mentioned on the main page. This phenomenon will tend to result in variations of different period co-existing, which will make the underlying existence of only "whole number" periodicities much less obvious.

So, while the above is by no means a proof, I think it is reasonable to postulate the following:-

The periodicity of the Saros-Inex Panorama, and its variability over time, is the result of two processes which have [seemingly] entirely different mechanisms but almost identical results: the necessity for the intervals between Saros series with larger numbers of eclipses to be an integral number of [anomalistic] years, and the presence of a subtle interaction between Sun, Earth and Moon which causes a slight oscillation in the orbital position of the Earth, whose period and variation can be predicted from lunar orbit theory. I am doubtful whether the very close correspondence between the consequences of these two effects can simply be a coincidence, but have no idea how they could possibly be related - definitely a challenge to be taken up by someone with more theoretical knowledge than I!