The Orbit of the Moon
Introduction
The Earth's Moon is, in many ways, an unusual member of the Solar System. With the exception of Charon, the major moon of the dwarf planet Pluto, it has, by far, the largest size compared to its parent of any moon in the Solar System [1]. It is also quite large from an absolute size perspective, having over two-thirds of the diameter of the planet Mercury. Its orbit is equally unusual, as it lies almost in the plane of the Ecliptic rather than of the Earth's equator: as far as I have been able to determine, Neptune's small moon Nereid is the only other moon of any other planet to show this behaviour (of which more anon). Furthermore, the Moon's orbit also has a considerable eccentricity, which is not the case for the large moons of other planets, and a very long period as compared to that of its parent.
To put some numbers on the above, the Moon has a diameter 27.3% of that of the Earth while the next largest in relative terms (Neptune's moon Triton) is just 5.5% of the diameter of its parent. The Moon's orbit is inclined at an average angle of just 5.145deg to the plane of the Ecliptic, compared to the 23.4deg tilt of the Earth's equatorial plane. The extreme values are 5.304 and 4.981, reached when the line of nodes (the line joining the two points where the orbit passes through the Ecliptic plane) is parallel to the Earth-Sun line and at 90deg to it respectively. This is what you might expect, as the gravitational pull of the Sun will be able to decrease the tilt of the orbit more easily if the line of nodes is at 90deg. Also, the plane of the orbit is [basically] fixed in space i.e. it does not rotate in synchrony with the movement of the Earth round the Sun. However, due to the attraction of the Sun on the Moon's relatively massive body, the line of nodes does go round clockwise (a process called "regression") with a period of 18.61yrs - very quickly as compared to planetary orbits. The present mean value of the orbital eccentricity is 0.0549, with extreme values of 0.026 and 0.0775. In a similar way to the variation in orbital tilt, the eccentricity is greatest when the major axis (the line joining the apogee and perigee points) is directed towards the Sun and least when the axis is at 90deg to the Earth-Sun line. Also as with the line of nodes, the major axis slowly turns but this time anti-clockwise (which is called "precession") with a period of 8.85yrs. Finally, the Moon orbits just 13.4 times per solar orbit of the Earth, compared to the 135.6 times of the next "slowest" (Saturn's moon Iapetus).
Both the inclination and the eccentricity, and indeed all the other parameters of the Moon's orbit, have short-period variations due to the disturbing influence of the Earth and the Sun, but this article will not be discussing those. What I am concerned with here is the reason for the anomalous mean values of (in particular) the orbital inclination and eccentricity, and how they might have changed (and will continue to change) over "geological time".
It will probably come as no surprise if I were to suggest that the above unusual factors might have a common cause, and in fact this would be true - though common causes is probably closer to the truth. There are three of major importance: the mechanism of the Moon's creation, the relative proximity of the Earth-Moon system to the Sun, and two forms of "spin-orbit coupling" between the Earth and the Moon. I shall thus firstly describe how it is thought that the Moon was formed.
The Creation of the Moon
There have been five serious theories suggested for the formation of the Moon:-
- By material flung off a rapidly-rotating Earth
- By gravitational capture of a body formed elsewhere in the Solar System
- By "co-creation" i.e. formation at the same time in the same place
- By the condensation of debris formed from the collision and breakup of asteroid-sized bodies orbiting close to the Earth
- By the condensation of a disk of material created in a collision of the proto-Earth and a large body which had formed in the same orbit as the Earth
Theory 1 is actually dynamically impossible and Theory 2 would tend to be ruled out by the very considerable similarity in composition between rocks on Earth and on the Moon and the low likelihood of such a body approaching sufficiently close to the Earth to be captured, although it is probably the explanation for the Pluto / Charon pair, whose compositions are likely to be different (if their surface colours are anything to go by: Pluto has a red tinge whereas Charon is more neutral grey), and which could have come close together because the furthest part of Pluto's orbit strays into the fringes of the Kuiper Belt of distant Solar System objects. Theory 3 is most unlikely to happen in practice, as two large bodies so close together would tend to coalesce during their formation, and it's not clear how Theory 4 would produce such a large satellite for the Earth. Theory 5 is the currently accepted method, which in detail says that when material was blown into space 4.45 billion years ago by a relatively low-speed, glancing, impact on the proto-Earth of a Mars-sized body, usually called Theia, orbiting in almost the same orbit as the Earth, some of it would have been captured by the Earth's gravitation and rapidly (meaning, remarkably, in only some tens of years or perhaps a century) coalesced into a solid body - the Moon. [Note that this theory does not require Theia to have been formed close to the Earth but simply at about the same distance from the Sun].
There is no way of telling directly what parameters the Moon-forming collision would have left the Earth-Moon system with, but if we assume that the planets were formed by accretion from a thin disk of material lying in the Ecliptic plane, symmetry considerations would indicate that before the collision the proto-Earth would probably have been spinning more-or-less upright, as Jupiter and Mercury, the only planets whose rotation axes are thought to have led a fairly undisturbed "life" since the formation of the Solar System, still do today. The collision could not have simply "knocked the Earth over", as disturbing a massive rotating body causes its spin axis to precess (i.e. describe a conical motion, as observed with gyroscopes) rather than changing its inclination greatly. This would also be true for the material ejected by the collision - its original rotation direction would be preserved to some extent, leading to a tendency for it to continue to orbit in the plane of the Earth's equator. It is probably reasonable to guess therefore that after the collision the newly-enlarged Earth would be spinning at a small angle to the vertical rather than a large one and that the Moon would be orbiting more-or-less in the plane of the Earth's equator (which of course, because of the presumed small axial tilt, would also be not that far off the plane of the Ecliptic). In fact, numerical simulations of the collision and of scenarios that would have evolved into the present situation are consistent with the tilt of the Earth's axis being about 10deg (off vertical) shortly after the formation of the Moon, with the Moon orbiting very close to the Earth's equatorial plane (i.e. inclined at about 10deg to the Ecliptic).
Evolution of the Orbit
Immediately after its formation the Moon would have been about 20,000km distant and orbiting in about 5hrs: the Earth would have rotated with about the same period. Massive tidal effects would then have raised "bulges" on both Earth and Moon, causing dramatic changes in their separation and spin & orbital periods due to the transfer of spin angular momentum from the Earth to orbital angular momentum of the Moon. The result is that the Moon would have moved away from the Earth and increased its orbital period, and the Earth would have slowed its rotation. In addition, the spin of the Moon would have become synchronous with its rotation. These changes would initially have happened very quickly (by geological standards!) with the Moon reaching 75% of its current distance and 70% of its current orbital period in 1.5 billion years. A much steadier rate of change would then have prevailed (as the effects depend on the square and cube of distance) and of course are still going on today - the current rates are a recession of 38.247mm/yr and a slowing of the Earth's rotation by 2.3msec/century. I have explored this process in very great detail in my article "The Recession of the Moon", part of the larger article titled "Do We Really Need The Moon?".
While the recession of the Moon does not have a direct influence on its orbital inclination (though it does explain why the lunar month is currently so long), it does introduce a mechanism whereby a change of inclination could be brought about. In a similar way that conservation of angular momentum in the plane of the Ecliptic causes a link between the Earth's axial rotation and the Moon's orbital rotation, conservation in the direction orthogonal to the plane brings about a connection between the Earth's obliquity (axial inclination) and the inclination of the Moon's orbit. Tidal effects will again come into play as an agent of change, and of course the torque generated by the gravitational attraction of the relatively nearby Sun on anything not in the plane of the Ecliptic will also be important.
Following the establishment of the initial situation therefore, tidal and solar torque effects would begin to change both the mutual inclination between the Earth's axis and the Moon's orbital plane and the absolute inclination of the orbit with respect to the Ecliptic. The effects would need an asymmetry to work on, however, (in same way that the asymmetric pull of the Earth on the Moon due to the raising of "tidal bulges" on the Earth is the agent that couples the Earth's spin to the Moon's orbit) and the degree of mutual inclination implied by the assumed initial conditions is actually too small for the situation to evolve into the present position. The phenomenon which comes to our aid here is that of resonance, whereby a small force applied at exactly the same place in a cycle can produce a dramatically greater cumulative result than if it were to be applied at random intervals.
I said above that the line of nodes regresses with a period of 18.61yrs, and the line of apsides (joining the apogee and perigee points) precesses with a current period of 8.85yrs. These periods were much shorter when the Moon was much nearer the Earth, and it is thought that when the apsidal precession period became exactly equal to 1yr the Moon's orbit became seriously perturbed, greatly increasing its eccentricity (to about 0.5). A second resonance involving the nodal recession period and the Moon's orbital period kicked in very shortly afterwards, but it was quite weak and so while it increased the mutual inclination it did so by only about 3deg: not enough to permit spin/orbit coupling to take over. However, the large eccentricity would have produced a considerable difference in the Moon's distance from the Earth between apogee and perigee. The consequential variation in gravitational attraction would have caused the Moon to flex and distort as it traversed its orbit, heating it and thus causing it to soften. This would have increased the energy dissipated by tidal effects, influencing the orbit-changing processes. In particular, the eccentricity would begin to decrease and this in its turn would counter-act the increase in the Moon's separation from the Earth, eventually (but briefly) reversing it. This would set up favourable conditions for another pass through the nodal-period resonance, but this time it would be strong enough to increase the mutual inclination to around 9 to 12deg. This was now enough for the "spin/orbit coupling plus conservation of momentum plus solar torque" processes to evolve the situation towards what we find at present. The eccentricity would initially rapidly reduce (but would then slowly increase again due to the Moon's recession), the inclination would slowly decrease and the Earth's obliquity would increase fairly rapidly. The melting induced by the change in eccentricity could also provide a source of liquid rock which could seep out of cracks caused by the flexing, thus producing the lunar mare we see today (which are otherwise difficult to explain).
The detailed and extremely complex calculations necessary to arrive at the above conclusions were first undertaken in 1998 by Jihad Touma and Jack Wisdom, of the McDonald Observatory, University of Texas, and the Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, respectively. There is an abstract of their work in Ref. [2], which has a link to the full text of their paper for anyone who is feeling very (very!) brave. This work in fact builds on earlier calculations by these authors and others, which had already determined the overall picture of the evolution of the Moon's orbit without addressing the problem of how to start the whole thing off: the discovery of the resonances solved this issue. See Ref. [3] for the earlier work.
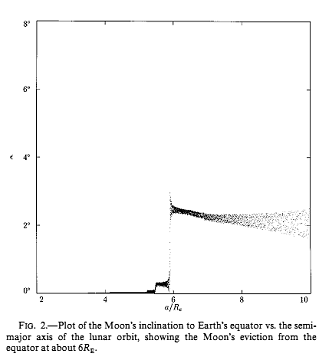
For those who believe that a picture is worth a thousand words, however, I have extracted some diagrams from each of these papers which nicely show both the effect of the resonances and the overall picture. Note that the x-axis in each of them is in units of the Earth's radius - the points marked "6" in the first three diagrams thus correspond to about 38,250km (a distance the Moon would reach in a mere 75 million years after its creation) and those marked "30" in the other diagrams to about 191,000km (reached in 784 million years).
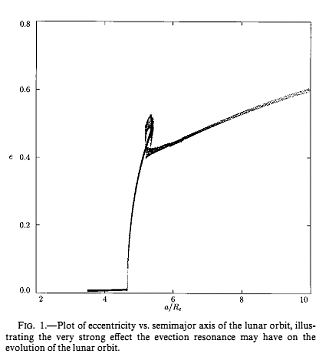 | These diagrams show the three passages through resonance mentioned above. The first (on the left) is the apsidal resonance, which causes the orbital eccentricity to suddenly increase, and the second & third (below) are the two passes through the nodal resonance, which cause jumps in the inclination of the orbit to the Earth's equatorial plane. As can be seen from the x-axis scale, the dramatic changes triggered by the resonances occur very soon after the Moon's creation, setting the scene for the subsequent more orderly development. |
 |  |
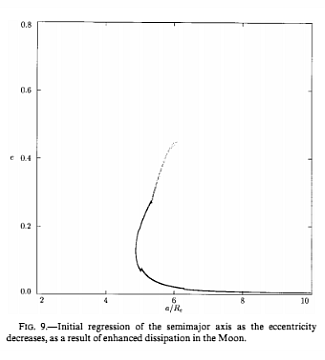 | Here we see how, as the eccentricity reduces because of the increased tidal dissipation, the steady increase in the Moon's distance from the Earth reverses for a short while, permitting the second passage through the nodal resonance seen above. |
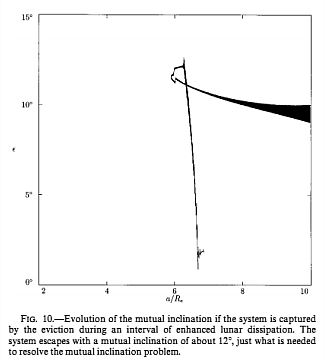
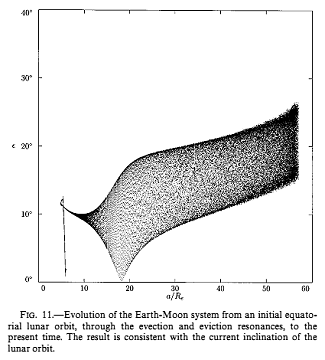 | This diagram shows how the mutual inclination changes after the resonances have set up the starting conditions: this is shown by the initial upwards spike. The diagram shows a band of values rather than a simple line because of the precession of the plane of the Moon's orbit, as mentioned above. This causes the mutual inclination to swing between O + I and O - I, where O is the obliquity of the Earth's axis and I is the inclination of the Moon's orbit. The mean value of the band is thus the obliquity and the width of the band is twice the inclination. At the far right of the diagram (representing the current situation) it can be seen that the obliquity is about 20deg and the inclination about 5deg. The former value is about 3deg too low, but this is mainly due to the initial values chosen rather than a fundamental problem with the simulation. |
 |  |
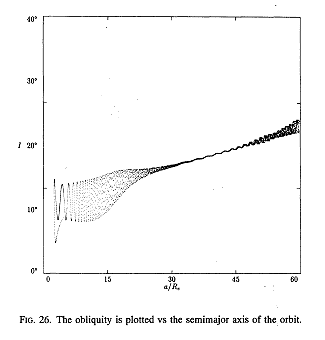 | These diagrams show the variation in the mutual inclination, the lunar orbit inclination and the obliquity of the Earth's axis as calculated in the 1994 paper (i.e. without considering resonances). It can be seen that without resonances the mutual inclination needs to start off at a totally unreasonable value. It is also notable that both the inclination & obliquity undergo a considerable period of oscillation before settling down: it is not clear whether this would be different in the "with resonances" case as no diagrams corresponding to Figs. 25 & 26 are given in the 1998 paper. |
Is the Moon actually a satellite body?
While, as I said above, the recession of the Moon does not of itself affect its orbital inclination, it does have the very important result of reducing the gravitational attraction of the Earth: this tends to bring the Moon increasingly under the control of the Sun rather than the Earth. In fact, at its current distance from the Earth (384,400km) the gravitational attraction of the Sun is 2.2 times that of the Earth (the point of equality is at 259,270km, reached after 1.25 billion yrs). It is therefore not unreasonable to claim that the Moon is now actually orbiting the Sun, rather than the Earth! In fact, because of the Moon's distance from the Earth and the extreme length of the lunar month as compared to the solar year, if one plots out the Moon's path round the Sun over an entire year it is found to be concave at all points: it certainly does not perform "loops" round the Earth, as diagrams (particularly animations) sometimes show, and even when passing between the Earth and the Sun its path is not curved towards the Sun. This characteristic of the Moon's orbit can be shown geometrically [4] and also proved mathematically [5], and is unique amongst all the other moons in the Solar System. Quite soon after its creation therefore the Moon became, effectively, a planet co-orbiting the Sun with (and perturbed by) the Earth rather than a satellite of the Earth: the tendency for its orbital plane to be gravitationally drawn onto that of the Ecliptic rather than the Celestial Equator is thus quite understandable.
All other planetary moons are so much smaller than their parent (even the Galilean moons of Jupiter, which are themselves of planetary size), and so much further from the Sun that the gravitational attraction of the Sun has little effect on them relative to the influence of their parent: one would thus expect them to orbit in the parent's equatorial plane. This is indeed generally true for all the closest moons of Jupiter, Saturn, Uranus and Neptune, with the exception of Neptune's large moon Triton. Those orbiting further out tend to be very small and have rather "odd" orbits, with high eccentricities and large inclinations, indicating they are most probably captured rather than co-created objects. Triton is almost certainly captured also, as it goes round in a retrograde orbit with a large inclination which effectively rules out co-creation. In fact, it is sufficiently close to Neptune that its orbital distance is slowly decreasing: it will thus eventually get torn apart (and probably form a ring) when it gets to the Roche Limit.
The stand-out exception to all this is, as previously mentioned, Neptune's moon Nereid whose orbital plane is at about 7deg to the Ecliptic (whereas Neptune's axial tilt is about 28deg) [6]. Nereid orbits "the right way round" and so might have been co-created, but the enormous eccentricity of its orbit (0.75) would tend to rule this out. Its most probable history is as a captured object whose orbit was subsequently disturbed by the arrival of the much larger Triton. The fact that it orbits close to the plane of the Ecliptic is thus likely to be due to chance rather than a specific causal mechanism.
Summary
So, to summarise. When the Moon was first formed it would probably have orbited nearly in the Earth's equatorial plane, but as the Earth would have had a much smaller axial tilt than now the Moon's orbit would also have been reasonably close to the Ecliptic plane. The transfer of angular momentum from the Earth's spin to the Moon's orbit due to tidal effects would have moved the Moon away from the Earth and at the same time slightly altered the relative tilt of the Earth's axis and the Moon's orbital plane. These changes then triggered two different resonance effects, the final outcome of which was to considerably increase the relative tilt. Further angular momentum changes could then work to enlarge this difference. However, because the Moon was by this time coming more under the influence of the Sun than the Earth, the pull of solar gravitational torques on the Moon's orbit caused the increase to mainly affect the Earth's axial tilt. Over time, therefore, the result was a considerable increase in axial tilt to the 23.4deg it is now but a slight decrease in the orbital inclination to the 5.145deg to the Ecliptic it is now. All these changes are still going on today, but much more slowly due to the greater distance between Earth and Moon and the slower spin and orbital periods of Earth and Moon respectively.

| References (Return to text) |
| [1] | Largest moons in the Solar System - Ian Ridpath |
| [2] | Resonances in the Early Evolution of the Earth-Moon System. The Astronomical Journal, Vol 115, No.4:1653-1663 - Touma & Wisdom |
| [3] | Evolution of the Earth-Moon System. The Astronomical Journal, Vol 108, No.5:1943-1961 - Touma & Wisdom |
| [4] | The Orbit of the Moon around the Sun is Convex! - Helmer Aslaksen, University of Singapore |
| [5] | The Moon Always Veers Toward the Sun - MathPages |
| [6] | Neptune and Triton. University of Arizona Press 1995 - edited by Dale P.Cruikshank. Footnote to page 85. |







