
Although JWS and OOS events are very and relatively uncommon respectively, the reason they happen at all is that the movements of the three inner Galileans (Io, Europa & Ganymede) are synchronised due to mutual gravitational attraction. This results in their orbital periods being almost exactly in the ratio 1:2:4 and (of more direct relevance to "events") their positions on their orbits, as seen from Jupiter, being precisely locked together. This means that they line up much more frequently than would be the case for a non-synchronised system. For example, Mercury and Earth return to almost exactly the same relative positions (as seen from the Sun) every 13yrs, and Venus and Earth do so every 8yrs. Therefore, all three planets will be simultaneously "back to where they started" every 13*8=104yrs. This period is massively greater than the orbital period of even the slowest-moving body, and the final re-alignment is not quite exact even then. Compare this to the case of the inner Galileans: due to synchronisation, their "return to position" interval is just 7.05days, barely different from the longest orbital period, and the re-alignment is precise. This means that OOS events happen much more frequently than might initially have been imagined.
The way the synchronisation of the orbit positions of the inner three Galileans operates has the following consequences:-
As well as the moons themselves transiting Jupiter, their shadows can also do so: this is the Jovian equivalent of a solar eclipse. Depending on the alignments, the moon its shadow or both objects can be in transit: one type of transit can also follow another, of course. Triple Transits involving shadows as well as moons are more common than those involving moons alone as the number of possible combinations is much greater. In the years 1981 to 2040 there are 21 such events (excluding the 10 mentioned above): 35 per century.
We can deduce from the above rules that there are just two unique ways that the three inner satellites can be non-visible: Io occulted while Europa & Ganymede are in transit and Io & Ganymede occulted while Europa is in transit (these patterns with "occulted" replaced by "in transit" and vice versa are also possible but they are simply the result of viewing the basic patterns "from the other direction" i.e. 180deg round the orbit). Analysis shows that these configurations occur alternately, 3.525 days apart i.e. exactly half of the 7.05 day re-alignment period for a given configuration.
The main thing that confuses the above analysis is that although the re-alignments of the inner three Galileans are precise, the position of each re-alignment point drifts a little relative to the previous one - by 5.8deg, in fact. In other words, if the inner moons were all exactly on the Sun-Jupiter line at a given time (i.e. were all exactly at inferior or superior conjunction) then 7.05 days later they will again all be in a line but that line will have rotated (clockwise) by 5.8deg. This will usually not be sufficient to move them far enough away from Jupiter (as seen from the Earth) to avoid being in transit or occulted, however, so another near-identical OOS event is likely to occur. This would also have been the case 7.05 days before the perfect line-up and may indeed be so for further periods of 7.05 days each way as of course one has to take into account the possibility of the moons being in eclipse rather than just occulted: the presence of Jupiter's shadow extends its "effective diameter" considerably. Eventually, however, the drift will take a moon outside even Jupiter's shadow and so the sequence of events will end. The next sequence will start when the drift moves the "line of alignment" back to where we started: the time between the mid-points of such sequences will clearly be 7.05*360/5.8=437.6 days. OOS events of a given type thus happen in groups, with 7.05 days between each member of a group and 437.6 days between the mid-points of each group. In practice, there will be from 3 to 5 events in each group.
If one had to rely on a "natural" alignment of the four Galileans then JWS events would practically never occur. However, because of the synchronisation, one is really only looking for a double alignment - Callisto with the "composite body" formed by Io, Europa and Ganymede. We found above that the three inner Galileans can be non-visible every 3.525 days and, as with the inner three, Callisto can be non-visible by being either in transit or occulted: there are thus two JWS possibilities per orbit of Callisto, not one. To find potential JWS events we must therefore look for coincidences between periods of 3.525days and 8.377days (half of Callisto's orbital period) rather than between 7.05days and the full orbital period of Callisto.
The smallest (accurate) such coincidence turns out to be 67 days (19 periods of 3.525 days and 8 "half-orbits" of Callisto) but of course this coincidence won't be aligned with the original line-up: the drift of 5.8deg per 7.05 day cycle means that after 19 "half-cycles" the alignment will be 55.1deg out. To duplicate the original line up would need a total drift of 360deg, but unfortunately this is not exactly divisible by 55.1 and so it is not actually possible to have two consecutive identical JWS events.
The precise number of half-cycles and half-orbits corresponding to 360deg is 124.138 and 52.245 respectively, each of which corresponds to 437.64 days - the same interval as discovered above. However, to get another line-up the number of half-cycles and half-orbits must both be whole numbers, and if we take 126 and 53 respectively the corresponding time periods are now very close - 444.21 and 443.97 days respectively. Because of the symmetry of the situation, a "theoretical" line-up will also occur after a total drift of 180deg rather than the whole 360deg, corresponding to a time interval of 218.82 days. However, this situation has the same problem as the previous case - 180 does not evenly divide by 55.1. The problem has the same solution though: if we take 57 half-cycles and 24 half-orbits we get periods of 200.95 and 201.04 days respectively. It should be noted that the average of these numbers, 201.00, is exactly equal to 3 times the smallest coincidence interval of 67 days.
We have thus discovered that "4-way" line-ups, which are what produce JWS events, can only actually occur at intervals of 201.0 and 444.1 days rather than the re-alignment intervals of 218.8 and 437.6 days. A full analysis of all the integer numbers of half-cycles and half-orbits shows that intervals of 134, 268, 335, 402 & 469 days are also possible. However, these are all, like 201, simply multiples of 67 and so we haven't really found anything new. There are no intervals corresponding to fractions of the 444 day period because its 53 half-cycle component is a prime number and so cannot be sub-divided.
The above analyses are correct only when considering the Jovian system in isolation, however. When viewed from the Earth, the timings are affected by the motion of the Earth relative to Jupiter between successive alignments. To avoid the need to consider the motion of both Jupiter and the Earth separately, it is useful to work with the period between oppositions of Jupiter (i.e. when the Sun, the Earth and Jupiter are in a straight line): this is almost exactly 400 days. If a JWS event happens to occur exactly at opposition, when all four Galileans re-align after 444 days the Earth will be 40deg past the previous straight line. This difference means that the view of the Galileans as seen from Earth will be somewhat different from that seen from Jupiter, and so at this instant they are unlikely to be in alignment again for a terrestrial observer.
One might think that the re-alignment period of 201 days would be very good news here, being almost exactly half the opposition period. After this time the Earth would have completed half an orbit of the Sun relative so Jupiter, and so there would be a straight line between the three bodies again, but now in the order Earth-Sun-Jupiter. Would this not mean that another JWS event would occur? But no - remember that the 201 day re-alignment period is relative to an observer on Jupiter, not to the Sun-Jupiter line. The "line of re-alignment" would have turned by only 165deg relative to the Sun-Jupiter line and so would not be pointing at the Earth again.
So, have we not proved that it is impossible to have more than the odd "chance" JWS alignment? Well no, as we only considered one particular situation in each case, but the analysis does show why they are quite rare. It also gives some clues as to situations which could produce other than random events.
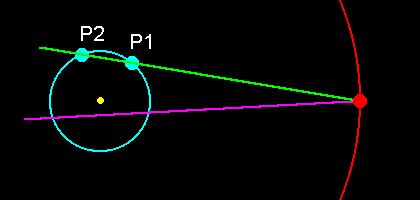
Firstly, consider the fact that a line drawn across a circle will cut it in two places. An observer on the Earth will thus be able to look along the same Earth-Jupiter line from two places on the Earth's orbit, not one. Clearly, for the Earth to move from the place which is nearer to Jupiter to that which is slightly further away it will have to traverse more than one complete orbit [or considerably less than one, of course, but we don't need to consider that option], which will take longer than one orbital period. This is exactly what we need, given that the longer re-alignment period (444 days) is greater than the opposition period (400 days). It would thus seem possible for there to be two JWS events separated by these 444 days as long as the geometry can be arranged correctly. A little thought will show that arcs spanning the points 90deg before and after the point of opposition would be the only candidates for this, as at just these places will the line-of-sight cut the orbit at two points relatively close together - remember that the Earth will have moved by just 40deg between the two events. The sight-line will also have moved slightly (as it completes one turn in 438 days rather than the 444 day re-alignment period) but not enough to upset the situation. I have illustrated all this by means of the diagram below.
 | The diagram shows part of the orbit of Jupiter (red) and the orbit of the Earth (light blue), drawn to scale. The green line is the line-of-sight from the Earth to Jupiter, showing that two positions, here P1 and P2, can share the same line. It is clear that the positions can only be close together if they are near to the 90deg before or (as shown here) 90deg after opposition points - compare the situation with that which would obtain if we took the pink line as the sight-line. For the Earth to move (anti-clockwise) from P1 all the way round the orbit and back to P2 would take longer than one opposition period, giving the possibility of matching this time with the re-alignment time of the Galileans. |
Thinking about possibilities for events separated by 201 days, note that when the Earth is close to the 90deg before and 90deg after opposition points there is a considerable Earth-Jupiter-Sun angle. This varies depending on the distances of Earth and Jupiter from the Sun, but averages just over 11deg. In other words, after the Earth has taken 200 days to traverse the 180deg required to move from close to 90deg before opposition to close to the 90deg after point (or vice-versa), the line-of-sight to Jupiter will have rotated by around 22deg. This value will decrease as the E-J-S angle reduces, as the Earth moves away from the 90deg points, and so there must be a starting position when the rotation exactly balances the shift of 165deg in the re-alignment line calculated above for successive 201 day alignments, giving rise to a further JWS event. However, given that the Earth orbits anti-clockwise and the re-alignment line moves clockwise, the geometry will only work if the Earth begins close to the 90deg after opposition point. Again, I have illustrated this by means of a diagram.
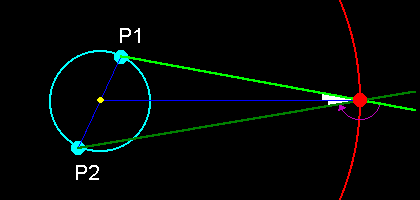 | As above, Jupiter is in red and the Earth is in light blue. We have seen that the alignment line (in light green as seen from P1) will take 201 days to rotate (clockwise) the 165deg indicated by the purple arrow, to lie as shown in dark green. During this time, the Earth has moved a fraction over 180deg (anti-clockwise) from P1 to P2. Because the Earth-Jupiter-Sun angles (shown in white) change according to the Earth's position on its orbit but can can be almost 12deg, there must be a situation when the shift in the line-of-sight as seen from the Earth is equal to 15deg (180-165), exactly compensating for the angle turned by the alignment line. It is clear that this will not work if the Earth starts off at P2 however, as a rotation of the dark green line by 165deg will leave it pointing nowhere near the Earth. |
The analysis therefore predicts that if a pair of JWS events should occur, the events will be separated by either 444 days or 201 days. Furthermore, in the case of successive JWS events separated by 444 days the Earth will be close to 90deg before opposition or 90deg after it at the time of the first member of the pair, and for events separated by 201 days the Earth will be close to the 90deg after opposition point. There is also the possibility of events separated by multiples of 67 days, but it is not clear how this might work out in practice.
There are a couple of consequences of the above predictions which can also be tested. As pairs of 444-day events must both begin and end close to the 90deg points and pairs of 201-day events must start close to the 90deg after opposition point and end close to the 90deg before point, it should be possible (providing all other alignment circumstances are correct) for there to be a further 444-day JWS event following either a first 444-day pair or a 201-day pair, and a 201-day event following a 444-day pair. It should not be possible to have consecutive 201-day pairs though.
But do these predictions agree with what actually happens?
To compare theory with practice, I calculated the time difference between those pairs of JWS events from 1900-2100 (as tabulated by Meeus) which occurred relatively close together in time. I was encouraged to find that, with very few exceptions, every difference was either 201 or 444 days, as predicted. There was one occurrence of 469 days, one of 226 days, and one of just 25 days. It should be noted that the value 469 arose in the earlier calculation of re-alignment intervals and is also 444 plus 25, and of course 226 is 201 plus 25. I'm sure it is significant that there were no instances of any of the multiples of 67 days other than 201 and 469 - it would seem that the correct geometry cannot be achieved for these intervals. Interestingly, when I extended the calculation to include all JWS events, not just those in pairs, I found that the difference from the previous event (however much earlier in time that was) could always be expressed as a sum of multiples of 444, 201 and 25 days. We have not come across 25 days so far, but it is the smallest period to be (almost) a re-alignment interval, being (approximately) 7 times the 3.525day alignment period (24.68) and 3 times the half-orbit time of Callisto (25.13).
I also calculated the number of days from opposition at which the first event of each pair happened, as this is a crucial element of my predictions. Of the seven 444-day pairs, six fell into the range 84deg before opposition to 99deg after it and the seventh was way outside this range (168deg before opposition) and so was probably a "random" alignment. However, the distribution of the values was not even - they tended to cluster around 55deg before and after opposition, with a gap at opposition itself (though this tendency was rather weakly defined, due to the small number of events in the dataset). Of the nine 201-day pairs, eight fell within the range 58 to 152deg after opposition, with a fairly even distribution and a mean of 101deg. The ninth pair was way outside this range (137days before opposition) and so was again probably a "random" alignment. It can thus be seen that "real life" does provide positive support for my theoretical analysis - quite strongly in the case of 201-day events but somewhat less so for 444-day events.
I then considered "triples" of events rather than just pairs, to test the "one interval followed by another" predictions. There were just three of these, two which were 444+201 and one which was 201+444. The small number of examples makes it hard to draw firm conclusions of course, but the existence of any triples at all is clearly strong support for the "one begins where the other ends" principle and the fact that none of the triples were 201+201 does tend to confirm my analysis of 201-day alignments.
All in all then, I feel that the list of events as presented by Meeus does tend to confirm my analyses of JWS intervals and alignments, at least as far as the most common event-types are concerned. As we have seen, there will always be a small number of "non-standard" alignments whose occurrence is difficult to predict, but I am happy that I was able to find plausible explanations for the majority of JWS events.
And just to wrap things up, here's a few comments on some topics I haven't considered so far.
It is noticeable that there is quite a large spread in the before/after opposition values. This can be explained by considering the "leeway" that exists in all line-ups i.e. the fact that a JWS event can occur in practice even though the line-up situation is not perfect. As mentioned in connection with OOS events, there are two main reasons for this. Firstly, because Jupiter is not a "point object", there is a small but definite range of positions where a Galilean can be non-visible (either occulted or in transit) despite not being perfectly aligned with the centre of Jupiter as seen from the Earth. Secondly, when Jupiter moves away from opposition it casts a shadow into space due to the angle that develops between the direction of illumination (Sun-Jupiter) and the direction of view (Earth-Jupiter). This angle can be almost 12deg (as previously mentioned), and so the shadow can extend a long way to the side of Jupiter and thus provide a considerable opportunity for a moon to be non-visible by being in eclipse. This is particularly important in the case of Callisto - of the 45 JWS events from 1900 to 2100, it is in eclipse for 27 of them. In addition, one or more of the inner Galileans is in eclipse on 16 occasions. In fact, if eclipses were not possible there would only have been 8 JWS events in this period.
Note that the leeway does not affect the alignments themselves. The re-alignments after 3.525 and 7.05days are geometrically precise but, as we have found, the line of alignment will only rarely be directed exactly at the Earth. Leeway provides scope for approximate alignments to cause JWS events (as seen from the Earth) at times slightly before or after those at which the precise alignments occurred. It also provides a "time window" for the event rather than a single instant (as each moon has its own range of positions, and thus times, when it is non-visible), thus potentially giving scope for a number of approximate alignments to come together. The situation is analogous to that which happens with solar eclipses. In very few cases does the centre-line of the Moon's shadow pass exactly through the centre of the Earth, but because the Earth is a physically large body it does not have to - somewhere on its surface will do. The Sun-Moon-Earth alignment thus does not have to be precise: a considerable mis-alignment will still produce an eclipse.
Given that the mis-alignment can be expressed as a difference in time from the "perfect" position, it follows that the time between events will not be exactly constant. For example, when I said that the time between JWS events was almost always 201 or 444 days, I did not mean that number of days exactly: in the case of 444 day events the variation is as much as +/-7hrs. In a similar way, although the time between solar eclipses is usually said to be either 29, 148 or 177 days, each interval has a considerable variation about these values: the range for 177 is actually +1.3/-0.9.
The 25 day interval probably appears for two different reasons. Firstly, given that there are only a few actual JWS intervals which are 25 days longer than the norm, one might put these down as "random" events, in the same way that I called periods before or after opposition which are way out of agreement with their peers random. However, I don't mean "random" in a mathematical sense but rather that these are alignments whose particular, very precise, circumstances it would be difficult to predict using the same sort of simple geometric considerations as I employed for the 201 and 444 day periods. The reason that 25 days appears in the sum comprising the difference between well-separated events is probably more to do with its own inaccuracy as a re-alignment period correcting for the small errors in the 201 and (particularly) 444 day periods. The "half period" and "half-orbit" versions of the (nominally) 201 and 444 day periods differ by +0.091 and -0.239 days respectively and so things would eventually get out of step were it not for the 25 day periods, which have an error of +0.452: note that this is positive, enabling it to balance the negative error of the 444 day periods. There is again an exact analogy here with eclipses: the usual (nominal) 177 day interval between them has a positive difference in its "new moon" and "node crossing" derivations which is compensated by the negative difference of 148 day intervals.
But enough of this theoretical analysis - let's get back to the actual observations!