Started in 1998 and continuously occupied since November 2000, the ISS is currently the largest space station ever constructed, at 120 yards by 80 yards - larger than a soccer pitch - and weighing around 415 tons. For further facts about the ISS, click here.
The orbit of the ISS has a height of about 250 miles and an inclination of 51.6 degrees to the equator. As a consequence of this inclination, locations with a latitude greater than this (i.e. most of the UK) can never see it pass directly overhead as it will always cross the sky somewhat to the south. As it orbits in the same direction as the Earth rotates, it tends to rise in the west, attain maximum height in the south and then set in the east.
The ISS's large flat solar-cell arrays are excellent reflectors of sunlight, with the result that it can appear as a very bright object in the sky. The brightness depends on the angle at which it is "flying" relative to the observer and to the sun (as this determines how reflective it is) and on the distance from the observer. The angles vary quite a lot because its attitude is actively controlled by on-board systems to, amongst other things, maximise power generation by ensuring the solar cells are pointing towards the sun. Also, because each orbit passes over an observer on a slightly different track, even if the ISS itself didn't move it would be presented to the observer (and the sun) at a different angle each time. The straight-line distance at the point of closest approach varies from about 250 to over 800 miles but when just rising or setting it can be as much as 1350 miles away. All this means that its maximum brightness on a pass over my location (Eastern England) ranges from about magnitude -0.2 to -3.8: a variation by a factor of over twenty-seven times! Passes which are easily visible (i.e. quite high in the sky) are very much towards the top end of the range, however. The other thing which is affected by distance is the speed at which the ISS appears to move. When it is low down (and thus far away) it moves really slowly but as it gets nearer and nearer its speed across the sky increases considerably so that at maximum elevation it can be quite difficult to track with a camera or through binoculars.
The ISS does of course need to be illuminated by the sun to be visible at all though, and this clearly can't be during daylight hours as the sun will be too bright to permit an observation, so in practice what is required is for the sun to have set (or not yet risen) as seen by the observer but still be visible from the ISS. This constraint means that there will tend be two distinct "windows of opportunity" for observation, one just after sunset and one before sunrise, though these can merge together in summer as the sun is then never far below the horizon. The Station will not necessarily be visible for the entire length of its track across the sky though, because it may be in sunlight for only a portion of its pass and so may move into the Earth's shadow before it goes out of view below the horizon. As with the same phenomenon when it involves the Earth's natural satellite the Moon, this is called "going into eclipse".
The ISS will not be visible every night because it takes about 93 minutes to orbit the Earth and so after 24 hours, when the Earth has revolved exactly once, the ISS will have made 151/2 orbits. In the 47 minutes the ISS needs to complete the last half orbit the Earth (and therefore the observer) will move 113/4 degrees further east, which will eventually take the observer out of the visual range of the orbit track. This will take a while though, as the "circle of visibility" has a radius of well over 1000 miles - this means you can see the ISS in the UK when it is actually passing south of the Alps! However, while this shift may take the ISS out of range for a late evening pass, for example, it may well be taking it back into range for an early morning pass. There will thus be distinct "seasons" of visibility: a run of days when it can be seen before midnight and then a sequence after midnight, separated by a period of no visibility when the orbit track is just too far away.
During a "season" it may be possible to see the ISS more than once on a given night. If the first pass is early in the evening for example, 93 minutes later there may still be enough sunlight to illuminate it a second time. Indeed, more than two consecutive passes may be visible in the summer as the sun isn't very far below the horizon then and so will be more able to illuminate the station. The theoretical maximum number of consecutively visible passes in a day is five because firstly there isn't much more than 6 hours (93mins times 4) of darkness in summer anyway and secondly the geometry of the circle of visibility dictates that if the first pass just clips the circle to the south-east it will take three futher passes before the fifth will just clip it to the south-west i.e. five consecutive passes (and no more) may all just have some portion of the track visible. For a visual proof of this, see the image below.
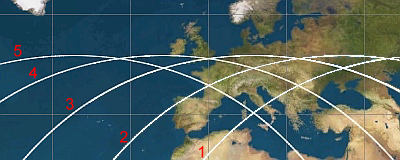
Here we have the UK in the centre of the image, with the ground tracks of five consecutive orbits shown. These move steadily to the west relative to an observer because in the 93 minutes it takes for the ISS to complete one orbit the Earth has rotated by 231/4 degrees to the east. Click or tap on the image to overlay a circle of the correct scale size to represent the area within which the ISS can be seen as long as it is at least 10 degrees above the horizon (based on the ground track diagrams given on the satellite tracking website Heavens Above). The circle has within it parts of all five ground tracks and it is clear that no further tracks would fit in, showing that five visible passes in one night is indeed the maximum number possible.
Simplistically, if the maximum number of consecutively visible passes in one day is 5 (which take 4 orbits from first to last) and each pass is offset by 231/4 degrees from the one before, the total offset between the first track and the fifth must be 93 degrees. So, as the track of the ISS moves by 113/4 degrees from day to day, it will take 7.91 days to move this amount, which should be the duration of a visibility season. In fact, a typical observation "season" is about 16 or 17 days because the situation is not so straightforward as detailed above.
Higher up the page I assumed that the observer's position on successive days would consistently move east because of the extra 47 minutes needed for the ISS to complete a whole number of orbits. However, instead of taking extra time to complete 16 orbits it is equally possible for the ISS to complete just 15 orbits and thus arrive 46 minutes "early". The observer's position would then be to the west of the ISS. Also, as we found above, it might be possible for more than one pass to be visible per day and we know that in those 93 minutes the observer's position will move considerably to the east. These variations give scope for more complex scenarios than just the simple "always to the east" situation previously assumed.
To investigate this matter further I transferred the timings of successive visible passes during the "visibility season" running from 19th October to 4th November 2024, as given by the Heavens Above site, into a spreadsheet and calculated the interval between them in terms of both time and orbits. The result was interesting, and not at all regular! The most obvious finding was that there were many instances where the time of the first or only pass in a day jumped back, sometimes by several hours, relative to the time of the first pass the day before rather than being later. This would seem to be a consequence of there being a relatively short window when the sun is able to illuminate the ISS, and thus make the pass visible, without having risen above the horizon and thus make the sky too bright to see anything. The extra 47 minutes between corresponding passes from one day to the next can thus take the pass into the dawn period at one end of the window, making it not visible, while moving the pass one or more orbits earlier into the "able to be illuminated" end at the other and thus take over as the first visible pass of the day but much earlier in time.
The most common way this happened was to have a 15 orbit gap between the days rather than 16 as mentioned above, though there were three cases of only 14 orbits and even one of just 13. A 15 orbit gap will mean the ISS arrives 46 minutes "early" rather than 47 minutes "late", moving the whole sequence back by a full orbit-time of 93 minutes. This will then usually leave enough time for a further pass one orbit later but this is then so close to the "sunrise" end of the window that it triggers an even greater jump back the next day, achieved by the 14 (and 13) orbit intervals just mentioned, after which a single extra pass will again be possible. Interestingly, the sequence 15,1,14,1 contains 31 orbits, which in total take just a fraction more than one minute longer than 48 hours. This means that, embedded in the apparently random sequence of pass timings, there will be passes multiples of two days apart which occur at almost exactly the same time on each occasion. The times I tabulated have several examples of four passes each two days apart which happen at the same time, before the sequence is disrupted by "jump backs". Note also that if more than two consecutive passes are visible on a given day (as mentioned above) the orbits they represent must be deducted from the number which will occur between this observation window and the equivalent one on the next day. In other words, if three passes are visible after the first set of 15 orbits in the sequence above rather than just the one, the sequence becomes 15,3,12,1 rather than 15,3,14,1. This is so because these orbits would clearly happen anyway, whether or not the ISS was illuminated during the pass. Also, these extra visible passes would not affect the movement of the ground track of passes through the circle of visibility, and thus alter the length of a visibility season, for the same reason.
We know from the analyses above that the ISS being late results in the observer being towards the east relative to the ground track of the ISS during that pass. An equivalent way of saying this is that the ground track of the pass sits to the west of the observer. Clearly, the converse is also true - if the ISS is early the track of the pass will be to the east of observer. The practical result of the variations in timing mentioned above is therefore that instead of the ground tracks of successive passes moving steadily to the west, and thus moving outside the circle of visibility reasonably quickly (as assumed by the simplistic analysis), because of all the backward jumps their progress is sort of "two steps forward, one step back" which considerably increases the number of passes it takes before the ground track finally leaves the circle of visibility, lengthening the duration of a season of observable passes, as found.
The other effect of the pass times getting steadily, if erratically, earlier is that eventually the time falls outside the period when the sun is able to illuminate the ISS and so the passes cease to be visible. Eventually though, the times regress sufficiently that the passes enter the "illumination window" around sunset and so a further observation season begins, this time in the evening. In like manner, this season will also develop and end and then another morning season will begin, and so on.
So there we have it. Not so simple as stated on the previous page but that is often the case with apparently straightforward observations - there's a lot of complexity once you start digging into the details!
