Iridium Satellites - the maths!

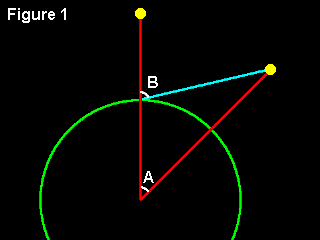
Before starting the full discussion I shall have to consider the concept I call "Parallactic Displacement": probably not the right term but it'll have to do for now! I mean by this the shift in observed elevation of a satellite due to a rotation of the plane of its orbit around a north-south axis. This can be an actual movement of the plane, due to variations in its orbit, or a relative movement, due to the Earth turning under it: the effect is the same. Figure 1 shows the geometry involved. It (and subsequent Figures) should be interpreted as a slice through the Earth at the level of the equator, viewed from above the North Pole: the Earth will thus rotate in an anti-clockwise direction. Placing the observer on the equator like this, and requiring all observations to be made directly east or west, makes the maths very much easier (3D trigonometry not being my strong suit!). Actual cases will differ in degree from this particular case but not in the principles involved.

Although the Figure is not to scale (the orbit height is actually about ¹/10 of the Earth's radius) it is clear that angle B [the parallactic displacement] will be much greater than angle A [the orbit rotation]. It is also clear that the magnitude of angle B depends on the orbit height: the lower the height the greater is B.

Close-in-direction flares

Successive flares produced by operational satellites can never be very close together in the sky because the rotation of the Earth during the (approx) 9 minute time interval between them causes the observed position of the orbit tracks to move across the sky. In-orbit spares provide a mechanism by which this shift can be compensated for, however - their lower orbit height means their observed elevation will always be lower than that of an operational satellite in the same plane. Consider, for example, flares seen to the west. Successive "9 minute" flares will get lower and lower in the sky due to the Earth rotating away from their orbital plane. If we add in a flare from an in-orbit spare, this will already be lower so the possibility exists that the next 9 minute flare will occur very close to it (how close will depend on the position of the Sun as well, of course, but I shall not take this into account here). There are two cases to consider:-

Relative to the Stars

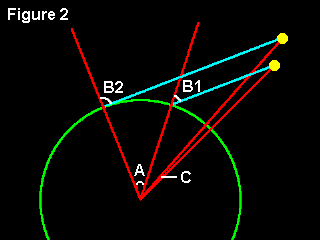For two flares to be close together relative to the stars the difference in the elevations of the two satellites at the times of the flares must equal the movement of the stars across the sky in the same period. It is, however, easier to work with the parallactic displacements, which are equal to (90deg-elevation). By reference to Figure 2, trigonometry shows that because the sight-lines must be parallel for the flares to be seen in the same place against the stars, the difference in the displacements (B2 minus B1) is equal to the angle A. This angle is just the amount that the Earth has turned between the flares (at 4mins per degree). To see what else this angle represents, imagine the observer is exactly on the Greenwich meridian (which of course moves with the Earth). Angle A is now the difference in longitude between the points where each satellite crosses the equator, plus or minus any slight difference in their orbital planes (angle C). Angle C will generally be small, but can't be ignored.

Relative to the Compass

The above analysis proceeded on the basis that the sight-lines must be parallel. However, it is clear by examining Figure 2 that solutions to the geometry may also exist when they are not parallel. In the case where B1=B2 (when the sight-lines will diverge somewhat) the flares will be seen in the same position in the sky as their elevations will be the same. I haven't done a detailed calculation for this case (more difficult!) but it is clear that a variation in the orbit height and/or equator-crossing times (i.e. angle A) and/or orbital plane difference will allow the geometry to be satisfied again. This seems to be true in practice, as examples of near-in-time flares at the same altitude and azimuth can occasionally be found on the HeavensAbove listings.

While it would in principle be possible for two satellites at the same height to satisfy the above criteria, in practice this cannot happen for the Iridium constellation because the time gap between successive satellites in the same plane would require a much larger orbital difference (angle C) to compensate for it. With satellites at different heights, however, the geometry can be satisfied by the much smaller differences that actually occur. Also, as the lower (spare) satellites do not have a fixed time relationship with the higher (operational) ones a solution to the geometry will be possible for a larger range of orbital parameters (and so is more likely to happen).

Daily Periodicity

The 24hrs minus 6mins periodicity happens in the following way. Iridium satellites do about 14.34 orbits a day so after 24hrs a given satellite will have 0.66 orbits to go to get back to its original position: this corresponds to 66.27 minutes (at 100.4mins/orbit). However, because satellites in a plane are separated in time by 9.13mins, the satellite 8 places forward will have "overshot" the correct position by 6.77mins [ 66.27 - 9.13 x 8 ]. Moving things back by 6 or 7 mins, therefore, will result in an exact re-alignment - re-calculating with the precise numbers gives us a period of 24hrs minus 6.98mins. However, this calculation assumes an ideal case. In practice the actual orbital parameters are a little bit different, mainly because the Earth is not a perfect sphere, and of course the flare cannot happen in exactly the same point in space as the Earth has moved round the Sun a little after a day and so the Sun-satellite-observer geometry will have changed slightly. These refinements change the re-alignment period to the 24hrs minus 6mins figure stated (plus or minus a few seconds).

Repetition of Ground Track

At the 24hrs minus 6mins point the Earth would still have to turn the final 1.5deg necessary to complete its daily rotation. This would cause the ground track to shift to the east by the same amount were it not for the fact that the Earth moves almost 1deg round the Sun daily (which would cause a westward shift, as the orbits are fixed relative to the stars not the Earth) and the orbit planes of the satellites themselves also shift westwards by almost 0.42deg due to the non-spherical shape of the Earth (a phenomenon called precession). Once again, the "real-world" figures are slightly different and mean that the ground track actually moves west by just a very small amount each day. Note however that a small change in ground track will produce a much larger change in observed position because of the satellites' relatively low orbits. Even so, the position of the flares will only differ by 1 or 2 (compass) degrees from day to day.

Movement against the Stars

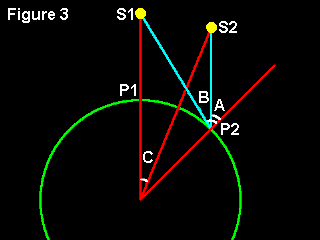The flares will move very much less relative to the stars than relative to the compass. Because the passage of the Earth round the Sun effectively turns it by about an extra 1deg per day, an angle it itself takes 4min to accomplish, a star directly overhead on one day [observer at point P1] will be overhead again after just 24hrs minus 4mins, not the full (solar) day. Thus 2min previously, i.e. at the 24hrs minus 6mins point calculated above [P2], the star will be 0.5deg [angle A] away from the overhead point (to the east, as the Earth rotates from west to east). A satellite aligned with this star on the first day [S1] will be seen far more than 0.5deg away from overhead on the second day though, as it is much nearer to us: this is the phenomenon of parallax, as illustrated at the top of this page. A little trigonometry shows that for an Iridium satellite the parallactic displacement for an observer at the equator [angle B] is almost 4.8deg. However, the magnifying properties of parallax also mean that to regain alignment with the star the satellite does not have to move the plane of its orbit by this amount - in fact it needs to move just 0.46deg (to the west) relative to the centre of the Earth [angle C, i.e. move from S1 to S2]. As stated above, the orbital plane actually precesses by about 0.42deg westwards daily so in fact the alignment is almost exactly re-established. [ Doing things more accurately does not change this conclusion ].