Solar Eclipse Durations: the tricky stuff!
As I said on the previous page, the duration of an eclipse is determined by shadow size and shadow speed. I shall consider the size factor first. Because neither the Earth's orbit round the Sun nor the Moon's orbit round the Earth are perfectly circular the distance of each from the others varies. In addition, the orbits are not exactly constant and so the distances of maximum and minimum approach also vary. The apparent sizes of Sun and Moon as seen from the Earth thus change quite a lot: this results in a considerable variation in the shadow width and hence the duration of eclipses. The size of the Moon has the greater influence as it varies by about 13% whereas the Sun varies by only 3.5%. This variation has a slightly asymmetric effect, however, because when both the Sun and Moon are at their average [apparent] size, the Moon is slightly smaller than the Sun. This is why there are somewhat more annular eclipses than totals and is also the first reason why annular eclipses tend to be longer than totals: on average, the Moon has to move further to clear the Sun's disc during an annular eclipse than during a total. The place on the Earth's surface where the eclipse occurs also has a bearing because as the poles are slightly further from the Moon than the equator an observer there will see a slightly smaller Moon. This will decrease the duration of a total eclipse but increase that of an annular. [The reduction in apparent size of the Sun has an opposite, but much smaller, effect].
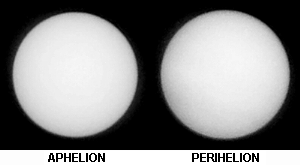
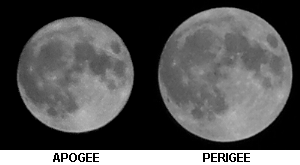
These pairs of images show the variation in size well: they are genuine images taken at the actual circumstances noted, not just scaled up and down from a standard template. The change in size of the Sun is almost undetectable but that of the Moon is quite dramatic.
This pair are composites of the largest Sun plus the smallest Moon (left) and the smallest Sun plus the largest Moon (right) - the Sun has been coloured pink to contrast it with the Moon. I think it is clear that the margin round the Moon on the left (a maximum annular eclipse) is just slightly greater than that around the Sun on the right (a maximum total eclipse).
The speed factor is affected by the Moon's orbital speed and the Earth's rotational speed. Due to the fact that its orbit is not a perfect circle, the Moon does not go round the Earth at a constant speed: in accordance with Kepler's Second Law it moves more slowly when further away. The consequence of this is the second reason why, on average, annular eclipses (which occur when the Moon is furthest away from the Earth) are longer than totals - the shadow moves more slowly. The Earth's rotation is constant but the effective speed of a point on its surface changes according to its latitude: on the equator it is about 1000mph but at the poles it is zero. To understand this, consider the fact that the farther you go away from the equator the smaller is the Earth's circumference at your latitude. This lesser distance still takes one day to traverse though, so the speed must be lower. This is important for eclipses because, as the shadow speed is the difference between the Moon's speed and that of the Earth, if one observes from a higher latitude the slower effective speed of the Earth means the shadow moves faster and so the eclipse will be shorter. Hope that's clear!
The influence of the solstices
To say that the shadow speed is the difference between the Moon's speed and that of the Earth is only literally true if the two effects are in exactly the same direction. However, the Moon's orbit is slightly tilted with respect to the plane of the Earth's rotation round the Sun and of course the Earth's axis of rotation is itself tilted: this is why we get seasons. Thus the angle between the track of the Moon's shadow and the line of the equator can vary a great deal (by +/- 28.75deg in fact), which has a dramatic effect on eclipse durations - in fact more so than the variations of distance. The best situation is when the relative angle is zero, and this can be achieved if the eclipse happens when Earth is just past or just before the solstice position so that its small tilt at that time matches that of the Moon's orbit. Because of the slightly different speed of the Earth at perihelion and aphelion, for maximal totals (which occur near aphelion, when it is moving slower) the critical difference is 13.45days and for maximal annulars (which occur near perihelion, when it is moving faster) it is 11.77days.
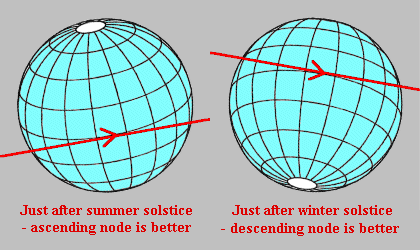As the diagrams on the right illustrate, the tilt of the Earth's north pole just after summer solstice is (when viewed from the Sun) slightly to the left i.e. the equator will slope up from left to right. This will compensate for a lunar orbit which is similarly inclined [shown in red]. Given that the Moon orbits in an anti-clockwise direction when viewed from the north (i.e. left-to-right when viewed from the Sun), the Moon will thus be moving in an upwards direction during the eclipse: this is called an "ascending node" event. Just before the same solstice the tilt is to the right, so the optimum situation now occurs at a "descending node" event. Clearly, a descending node eclipse just after summer solstice (or a ascending node eclipse just before) would have the tilts considerably mis-aligned, resulting in a shorter eclipse. Exactly the reverse is true just after winter solstice, as the Earth's tilt is to the right at this time. An ascending node event is now better before the solstice and a descending node event after it. Because it is equally likely that an eclipse will be ascending node or descending node and the "tilt matching" effect has such a great influence on durations, it is usual to calculate maxima for each type of eclipse separately.
Long-term cycles
Concentrating for a while on total eclipses, one would think that the longest possible total eclipse would simply occur when the Moon is at its largest (i.e. nearest to Earth) and the Sun is at its smallest (i.e. farthest away from Earth). These two conditions would be met if the Moon was at perigee exactly when the Earth was at aphelion (currently in early July). However, as described above, proximity to a solstice also has an effect: the overall optimum moment is thus a balance between the two factors, and so depends on the difference in date between summer solstice and aphelion. However, this slowly changes. Why? Well, the Earth's axis is not fixed in space but, like a wobbling top, describes a circle in 25,771yrs (a phenomenon known as precession): this causes the date of the solstices to get earlier by 1day every 70.56yrs. The Earth's orbit is not quite constant either (due to the perturbing effects of the Sun and planets) and so the point of aphelion is also moving, but in the opposite direction and more slowly. The two effects combine to give a shift of 1day about every 57.5yrs which, given that they were just over 13days apart in 2000AD, means that about 755yrs before then the summer solstice and aphelion actually coincided. At this date (1246AD, in fact), the optimum time was a fraction more than 7days after the solstice/aphelion point for ascending node events and the same period before it for descending node events. An eclipse exactly at the solstice would have had the same duration for both ascending and descending node events, but this would be shorter than at the optimum time as the tilts would be more mis-aligned.
As the centuries passed, aphelion slowly shifted later and later after the summer solstice, giving a period when ascending node events gave longer eclipses. The optimum eclipse date also moved, getting closer and closer to the date of aphelion: this meant that the maximum possible duration also increased. In 2000, it was just over 14days after the solstice, just over a day after the aphelion point. Eventually, in 2019 in fact, the interval between aphelion and solstice will equal the critical value quoted above (13.45days), when the tilts will automatically exactly cancel out [for annular eclipses the corresponding date is/was 1922]. At this point, a "maximally optimum" total eclipse could occur at the aphelion date, with the shadow moving parallel to the equator and the Earth as far as possible from the Sun. To read about another interesting sidetrack thrown up by my investigations of this situation, click here. In the future, aphelion and the solstice will move further and further apart thus making even a near match between the Earth's tilt and that of the Moon's orbit impossible: eclipses in general will thus get shorter. This trend will only cease when aphelion has gained 3months on the solstice, aligning it with the autumn equinox. At this point the tilt of the equator is just over 23deg, meaning that the minimum tilt mis-match is a whopping 18deg - this worst-case scenario will happen in 6429AD.
Things will then get better and better for another 5000yrs as aphelion shifts to 6months after the summer solstice. At this point it will move towards alignment with a solstice again, it's just that it's the winter one! This doesn't affect the "tilt cancelling" effect but does determine which hemisphere the maximum eclipse would occur in: northern for alignment with the summer solstice, southern for the winter one. It also means that the duration of maximum eclipses will be shorter than at the corresponding alignment with the summer solstice, as the Sun will be nearer at winter solstice and hence larger. Note also that after passing the equinox we are not so much after the summer solstice as before the winter one but, as shown above, it will still be the ascending node that produces the longer eclipses during this period. The point of exact alignment with the winter solstice produces a "1246AD" effect again (for the same reasons) before we enter a second phase of worsening maxima, but with the descending node dominant as we are now in the "after the winter solstice" position. The maxima will then steadily improve as we pass through the spring equinox and head back towards alignment with the summer solstice again to complete the entire 21,000yr cycle.
With "perihelion" substituted for "aphelion", "winter" for "summer", "autumn" for "spring" etc., the situation for annular eclipses is exactly similar, as the tilt mis-match influences the shadow speed but not its size. It remains true that maximum eclipses will be shorter at the mid-cycle (summer) solstice alignment, as the Sun is now further away than at winter solstice which makes annular eclipses shorter. However, because the critical number of days between perihelion and solstice for a maximally optimum annular eclipse (11.77) is smaller than that between aphelion and solstice for a maximally optimum total, the important date for annulars in our part of the current cycle is/was earlier - 1922 in fact, as mentioned above.
Very long-term variations
Superimposed on the above pattern is a general trend to shorter eclipses because the decreasing eccentricity of the Earth's orbit is making its aphelion smaller and its perihelion larger. Historically speaking, we're not in a good period for long eclipses at the moment, as the eccentricity is currently well below average and has been falling almost continuously for the last 100,000yrs. It will continue to decrease until it reaches a 2million-year low in about 30,000AD before beginning to rise again. Not really an issue for mere mortals, however!
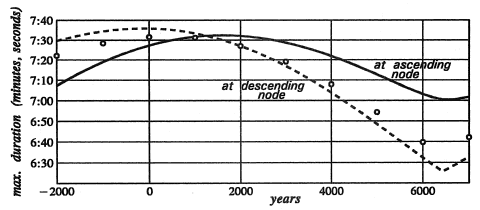Almost all the points made so far are illustrated by this diagram (taken from Meeus). The two curves show the different behaviour of ascending node and descending node total eclipses: they cross at 1246AD, as detailed above, when aphelion coincides with the summer solstice. The open circles show the effect of the decreasing eccentricity: they represent what the value for the descending node would have been at constant eccentricity (the value in 2000AD). The upturn in the curves just after 6000AD is the begining of the phase where aphelion is moving from alignment with the autumn equinox (at the minima in the curves) to alignment with the winter solstice. It is just about clear that the slope of the descending node curve is greater than that of the ascending node curve at this point, showing that they will eventually cross over again in a repeat of the pattern of the left-hand part of the diagram around the time of winter solstice, but with lesser maximum durations (as described above). The graphs for annular eclipses are very similar - although their shape is different in detail the overall behaviour is exactly the same. In particular, they also cross over in 1246AD but of course it is the descending node that becomes dominant after that time, not the ascending node, as it is perihelion coinciding with the winter solstice in that year that determines the development of annular eclipses.
Incidentally, at face value the date when aphelion and summer solstice coincided in 1246AD should have been 1st July. However, our current calendar uses a year (the vernal tropical year) that is just a little shorter than the time taken by the Earth to orbit the Sun (the sidereal year), which results in the equinoctial precession being "cancelled out". This is mainly for practical reasons, so the seasons don't drift round the months, but was initially set up so that the date of Easter could be strictly defined! It does also mean that the solstices remain fixed in the calendar and so it is just aphelion and perihelion that move: aphelion and summer solstice thus actually coincided on the calendar date 21st June 1246. [Further nerdy comment - These dates actually refer to our current (Gregorian) calendar: the one in force in 1246 (the less accurate Julian one) steadily got out-of-step with "real time" so 21st June (Gregorian) would actually have been 15th June (Julian) at the time. Click here for a very full description of calendar adjustment!].
An unexpected northern preference
The final factor that must be taken into account for any eclipse is a geometrical one. As mentioned right at the top of the page, the contribution the Earth's rotation makes to reducing the shadow speed is greatest for a point exactly on the equator. In general, though, the equator is not the nearest point to the Sun - at the summer solstice (when the longest totals happen) the north pole is tilted towards the Sun and so the near-point is the tropic of cancer. However, if you move away from the equator towards the tropic (i.e. north) in order to get nearer the Sun and thus enlarge the shadow (so making the eclipse longer), the shadow speed will also increase (because of the reduction in the Earth's rotation speed away from the equator) which will have the opposite effect: there is thus a trade-off. It turns out that the optimum northerly latitude shift is about 4.9deg, but the difference this adjustment makes is actually quite small - about 1.5sec. At the winter solstice, when the longest annulars happen, the south pole is towards the Sun and so the tropic of capricorn is the near-point. However, because the shadow for annulars gets larger as you move away from the near point, to increase the shadow width you must again go north of the equator, which leads to the same trade-off. These observations taken together mean there is a definite bias for long eclipses to be in the northern hemisphere. In fact, of the "long" eclipses of both types listed on the NASA website (i.e. totals greater than 7min, annulars greater than 11min), 63% are in the northern hemisphere. The mean latitude averaged over all 124 events is 3.3deg north.
