The Recession of the Moon
Introduction
It is a well-established observational fact that the Moon is moving away from the Earth at a current rate of about 38mm per year. This value is now known very accurately because of work done to monitor the Earth-Moon distance using a laser beam bounced back from reflectors left on the surface of the Moon by the Apollo astronauts, but the recession was noticed by early astronomers because of the effect the increasing distance has on the orbital speed of the Moon, resulting in it not being in the "correct" position in the sky. It is also the case that the length of the day is increasing, currently by 2.3 milli-seconds per century. This has been determined from the comparison of the time indicated by the position of the Sun with the time recorded on very accurate atomic clocks, but again was first noticed because of discrepancies between the recorded and theoretical times of historical solar and lunar eclipses. Finding a reason for these facts has attracted the attention of mathematical astronomers for several centuries!
Basic Principles
 Although those who have read my article on The Tides[1] will know that this terminology is not strictly accurate, the Moon-distance increase is normally explained via the agency of the tidal bulges (both in the oceans and in the solid body of the Earth) which, as shown by this diagram, are pulled forward of the Moon by frictional drag as the Earth rotates in the direction of the yellow arrow. The gravitational attraction of the nearer bulge for the Moon, shown by the green arrow, is therefore in front of the centre-to-centre line and so would be in such a direction as to have a component along the Moon's orbit. This would speed it up, leading to an increase in the size of its orbit [If you are not clear why this should be so, my article on Orbital Dynamics explains the physics of this situation]. The energy required to achieve this speed-up is taken from the rotational energy of the Earth, thus accounting for the slow-down in its spin rate. In addition, dissipation of additional energy by the tides enables sufficient angular momentum to be transferred to the orbit of the Moon from the spin of the Earth as this gets steadily slower. In principle, therefore, one ought to be able to calculate the rates of recession and slow-down due to the transfer of energy and momentum by working out the torque exerted on the Moon by the bulges.
Although those who have read my article on The Tides[1] will know that this terminology is not strictly accurate, the Moon-distance increase is normally explained via the agency of the tidal bulges (both in the oceans and in the solid body of the Earth) which, as shown by this diagram, are pulled forward of the Moon by frictional drag as the Earth rotates in the direction of the yellow arrow. The gravitational attraction of the nearer bulge for the Moon, shown by the green arrow, is therefore in front of the centre-to-centre line and so would be in such a direction as to have a component along the Moon's orbit. This would speed it up, leading to an increase in the size of its orbit [If you are not clear why this should be so, my article on Orbital Dynamics explains the physics of this situation]. The energy required to achieve this speed-up is taken from the rotational energy of the Earth, thus accounting for the slow-down in its spin rate. In addition, dissipation of additional energy by the tides enables sufficient angular momentum to be transferred to the orbit of the Moon from the spin of the Earth as this gets steadily slower. In principle, therefore, one ought to be able to calculate the rates of recession and slow-down due to the transfer of energy and momentum by working out the torque exerted on the Moon by the bulges.
However, this requires an accurate knowledge of the size, shape and position of the bulges to be able to calculate their gravitational attraction. While this should not be too difficult to determine in the case of the bulges in the solid body of the Earth (as they approximate the theoretical case very closely), it would be almost impossible to do the same for the oceanic tidal bulges as their size and distribution is very different from that which simple theory would predict (as shown in my article on The Tides). It is therefore necessary to approach the problem from a different direction, the most obvious of which is to determine the tidal dissipation and use this to calculate the amount of transferred angular momentum. However, the dissipation figure is not known from direct measurement as there is no practical way this could be achieved: early estimates were thus considerably in error, both above and below the currently-accepted value. Improvements in tidal theory and the advent of computers have now allowed the dissipation to be calculated from mathematical models which are constrained by measurements taken from ocean-observation satellites such as TOPEX/Poseidon [2]. The dissipation can of course also be deduced from the slow-down in the Earth's rotational speed it causes, so that is the first thing I shall now consider. [Note that, in all the calculations below, because the effects described are relatively slight, even over the one million-year timespan used, I have felt it necessary to quote what would in other circumstances be an unreasonable number of significant figures. This should not be interpreted as meaning that the values are accurate to this level though: the base parameters are usually not known to more than about 5 significant figures.]
Tidal Dissipation
Careful measurements with atomic clocks show that the day is apparently getting longer, which is the observable consequence of the slowing spin rate of the Earth. The loss of rotational energy this implies is caused by tidal frictional effects between the oceans and the landmasses and in the flexing of the Earth's solid structure. The lost energy is almost all dissipated as heat - the amount of energy transferred to the Moon to cause its orbit to change is relatively small by comparison (as we shall see below). The calculation required to work out the rate of energy loss needed to cause the observed slow-down is quite straightforward, but it is actually easier to "work backwards from the answer", so I shall reveal that the rate of loss is 3.614 x 1012 Watts. This is greater than the figure quoted in the Tide Heights page in my article on The Tides because it is the total figure taking into account all the tidal components, both oceanic and in the solid body of the Earth. The tide height calculations made use of the major lunar oceanic component only, which contributes about 2/3 of the total.
One Watt is one Joule of energy per second, and so in one million years the amount of loss stated above will reduce the Earth's rotational energy by (3.614 x 1012) x (60 x 60 x 24 x 365.2425 x 106) Joules = 1.140562 x 1026 J. The Earth's rotational kinetic energy is currently 2.137279 x 1029 Joules (calculated as 1/2 times its Moment of Inertia times the square of its rotational speed), so after one million years the tidal dissipation will have reduced it to 2.136139 x 1029 Joules. Assuming the Moment of Inertia remains unchanged, this equates to a rotation rate of 7.2902 x 10-5 radians per second or a rotational period of 86187.1 seconds. Subtracting the current [sidereal] rotation period (86164.1sec) gives the slow-down in seconds per million years due to tidal friction. The result is 23.0 (or 2.3 milliseconds per century), which is the accepted value.
Note that the other commonly-quoted figure, 1.7 milliseconds per century, is the actual current net rate of increase in the length of the day after taking into account such factors as the slight decrease in the Earth's moment of inertia due to its change in shape caused by the removal of the ice burden after the last Ice Age, which will cause the Earth to spin slightly faster. I shall discuss this and other related issues much later in this article.
If we now compare the calculated number with that quoted in Ref.2 for the total oceanic dissipation only (3.508 x 1012) [3] we see a difference of 0.106 x 1012 Watts. This is the amount of dissipation in the solid body of the Earth, exactly in accordance with the value quoted in the Tide Heights page. The calculation thus shows that the solid tides alone could not be responsible for the observed rate of slow-down as the dissipation they cause is far too small to achieve a sufficient effect. It also shows that the calculations of tide heights were done using a value for the dissipation which is consistent with the measured amount of slow-down of the Earth's rotation. The only very slight discrepancy is in the value quoted for the major lunar oceanic component: 2.421 x 1012 Watts in the reference quoted in the Tide Heights page and 2.435 x 1012 Watts in Ref.3. This small difference is probably due to the different methods use to estimate the two values and is, in any case, only of the same order as some of the stated uncertainties in the estimates. It should also be noted that there is a very small amount of dissipation caused by tides in the Earth's atmosphere - this only amounts to around 0.010 x 1012 Watts though.
Angular Momentum
I said above that the reason the Moon's orbit changes as the Earth's spin rate decreases is a transfer of angular momentum from the Earth to the Moon. I shall now calculate the effect this transfer will have.
The spin angular momentum of Earth is equal to its Moment of Inertia (8.04 x 1037 Kg m2) times its rotational speed in radians per second. Its [sidereal] rotation speed is currently 2 x pi /86164.1, and so its momentum is 5.861892 x 1033 Kg m2/sec. Due to the increase in day-length of 2.3msec/century, as calculated above, one million years ago its rotational speed was 2 x pi / (86164.1 - 23) and so its angular momentum was 5.863457 x 1033 Kg m2/sec. The difference is 1.565147 x 1030 Kg m2/sec, which is the amount that has been transferred to the Moon over this period.
The orbital angular momentum of the Moon is equal to its mass times its orbit speed times the orbit radius. To reduce this expression to a dependence on the orbit radius only, we note that in a circular orbit the square of the orbit speed is equal to the gravitational constant (G) times the mass of the Earth divided by the radius [The derivation of this result proceeds via the centripetal force being equal to the mass of the Moon times its orbital velocity squared divided by the orbit radius, and the gravitational attraction which provides this force being equal to G times the mass of both Moon and Earth, divided by the radius squared. I shall leave the algebraic manipulation as an exercise for the student!]. With a little further re-arrangement we find that the angular momentum is equal to the mass of the Moon times the square root of {G x mass of Earth x orbit radius}. Currently, the mean orbit radius is 3.844 x 108 meters so the angular momentum is 2.876908 x 1034 Kg m2/sec. One million years ago it must have been this value minus the difference in the spin angular momentum of the Earth i.e. 2.876751 x 1034 Kg m2/sec.
Now, Kepler's Third Law tells us that the orbital period squared is proportional to the orbit radius cubed and of course the orbital period is proportional to the radius and inversely proportional to the orbit speed. Given that angular momentum is proportional to orbit speed times orbit radius, a further heavy burst of algebraic manipulation tells us that angular momentum is proportional to the square root of the orbit radius. Another way of putting this is that the square of the ratio of two values of angular momentum is equal to the ratio of the orbit radii coresponding to these values. In the case being considered, the square of the ratio is 1.0001086 and so the orbit radius one million years ago was 3.844 x 108 / 1.0001086 = 384,358,175 metres. The difference is 41,824.5 metres, corresponding to an increase of 41.8245mm/yr over the one million year period. This should be compared to the value derived from laser-ranging experiments of 38.247mm/yr. One possible reason for the slight difference is the fact that the orbit radius did not suddenly jump from one value to another but had to undergo a continuous process of change as the orbital parameters were slowly altered. As my article on Orbital Dynamics illustrates, this causes the size and eccentricity of the orbit to change substantially as first the apogee and then the perigee of the orbit is affected. The above equations are only exactly true for circular orbits and so the eccentricity will cause a slight discrepancy. Another possible reason is that the Moon does not orbit in the plane of the Earth's equator and so any forces linking the spin angular momentum of the Earth and the orbital angular momentum of the Moon will be somewhat "off-centre", leading to a loss of efficiency in the transfer of energy and momentum: I consider this idea further in my article 'The Stability of the Earth's Obliquity'. However, whatever the reason for the discrepancy, the calculated and actual values are clearly sufficiently close to prove the assertion that the recession of the Moon is caused by the conversion of spin angular momentum of the Earth into orbital angular momentum of the Moon.
Energy
The transfer of angular momentum from the Earth's spin to the Moon's orbit is only one half of the equation, however, as an input of energy is required to actually effect the change in orbit radius (just as it is in the case of a satellite or spacecraft). There are two sorts of energy to take in account: kinetic energy, due to the Moon's orbital speed, and potential energy, due to the Moon's position in the Earth's gravitational field.
The orbital kinetic energy of the Moon is equal to half of its mass times its orbit speed squared. But, as we found above, orbit speed squared is equal to G times the mass of the Earth divided by the orbit radius. Thus, orbital kinetic energy equals 1/2 times G times the mass of both Moon and Earth divided by the orbit radius. Currently, this comes out to 3.810893 x 1028 Joules. One million yrs ago the orbit radius was one million times 38.247mm smaller and so the kinetic energy was larger, at 3.811273 x 1028 Joules. The difference is 3.792137 x 1024 Joules.
Note that the kinetic energy decreases as the orbit radius increases, which is rather contrary to what one might expect from the usual description of how the gravitational attraction of the tidal bulges for the Moon speeds it up and so increases its orbit radius. The resolution of the paradox requires a further reference to my Orbital Dynamics article, which says that an increase in speed at one part of the orbit increases the radius of the diametrically-opposite part, not the part where the speed increase occurs. This means that, starting from an initially circular orbit, the orbit becomes elliptical with the perigee at the point at which the speed increase occurs and the apogee at the diametrically-opposite point. The apogee is the point at which the orbit speed is least though, and so as the orbiting body moves away from the point at which the speed-up occured its orbit speed will decrease, resulting in a decrease in kinetic energy. However, because the apogee point is further away from the orbited body than it was previously, the potential energy of the orbiting body increases as it moves towards it. The initial increase in kinetic energy is thus "traded off" for an increase in potential energy due to the increase in mean orbit radius.
The above process is of course a continuous one in the case of tidal acceleration, as the force on the Moon is present all along its orbit rather than as a result of a single rocket-firing in the case of a satellite. This means that the Moon slowly spirals outwards, changing its orbital parameters all the time. The basic principle still applies though - the local increase in kinetic energy caused by the pull of the tidal bulges is continuously traded off for a global increase in potential energy and thus mean orbit radius.
The trade-off is definitely a winning one, because potential energy is equal to G times the mass of both Moon and Earth divided by the Moon-Earth distance. It can thus be seen that the potential energy gained is exactly equal to twice the kinetic energy lost! In the case being considered there is thus a net gain of 3.792137 x 1024 Joules in the million years, meaning that energy is being transferred from Earth to Moon at a rate of 0.1202 TW. Thus, of the total tidal dissipation of 3.614 TW calculated above, just 0.120 TW is taken by the Moon as it moves away while 3.494 TW is dissipated as heat.
Note that the "Moon's share" of the total dissipation is very nearly the same as the dissipation in the Earth's body and atmospheric tides (0.106 TW plus 0.010 TW). It could thus be tempting to say that it's the dissipation due to the oceanic tides that provides the transfer of angular momentum and that due to the solid and atmospheric tides which transfers the orbital energy. This would be an unphysical interpretation though, as of course the Earth doesn't "know" how its spin energy is being dissipated and the Moon doesn't "know" where its (temporary) increase in kinetic energy is coming from. The fact that the numbers are nearly the same is just a numerical coincidence, not evidence of a causal link.
Interim Summary
The recession of the Moon is caused by the following set of processes:-
- The fact that the gravitational field of the Moon varies across the diameter of the Earth causes tidal bulges to be raised in the oceans of the Earth and in its solid body (and also in its atmosphere, though this effect is negligible by comparison).
- The tidal bulges are "held in place" by the gravitational attraction of the Moon and so the Earth is forced to rotate under and through them. The friction between the Earth and the bulges as it does so has two consequences: the bulges are moved slightly forward and energy is dissipated.
- The fact that the bulges are slightly ahead of the Moon produces a force on the Moon acting along the direction of its orbit. This increases its speed, giving it more kinetic energy. This energy is taken from the overall energy dissipated in the tides - the remainder of the dissipated energy appears as heat.
- The total energy dissipated by tidal friction is taken from the rotational energy of the Earth, causing its spin to gradually slow. This decreases its spin angular momentum.
- The angular momentum tied up in the Earth's rotation at its original speed cannot simply be lost (as it is a conserved quantity) and so the excess is transferred to the orbital rotation of the Moon. The force exerted by the tidal bulges, which transfers energy to the Moon, is also the mechanism by which the angular momentum is transferred from the Earth's spin to the Moon's orbit.
- As a result of the transfer of both energy and angular momentum to the Moon, its mean orbit radius increases. Its mean orbit speed thus actually decreases, but the loss of kinetic energy in its motion is compensated for by the gain of twice as much potential energy in its orbit as the size of the orbit increases.
- Tides are also raised by the Sun but, since the lunar tides are more than twice as strong as the solar tides, the solar tides have more effect on the height of the bulges than on their position relative to the Earth. The net influence of the solar tides is, in any case, zero because the times when they add to the magnitude of the lunar tides (at Spring tides) are balanced by the times when they subtract (at Neap tides) and the times when they pull the tidal bulges further forward, when the solar tide-generating force is aiding the effect of oceanic tidal friction, are exactly compensated by those times when they try to pull them backward, when the solar force works against tidal friction.
Although it is necessary to describe them sequentially, the above processes actually happen simultaneously and continuously. The overall result is that the spin of the Earth slows down (by 2.3 milli-seconds per century), the Moon recedes from the Earth (by 38.247mm per year), and the oceans warm up ever so slightly.
Evolution of the lunar orbit
Taken at face value, the above calculations could be taken to indicate that because the Moon is receding at 38.247mm/yr it would have been touching the Earth (i.e. its orbit radius would be 8108.1km, the sum of their radii) 3.844 x 108 - 8.1081 x 106 divided by 3.8247 x 10-2 years ago. This comes to 9.84 billion years, which is over twice the accepted age of the Earth-Moon system. Something is clearly wrong, and that something is the fact that the recession rate depends on the distance. That this is reasonable can be seen by considering the fact that a given amount of angular momentum transferred from Earth to Moon has a proportionately greater effect when the existing angular momentum to which it is being added is small i.e. when the orbit radius is small. In addition, it is also reasonable to assume that the amount of tidal dissipation, and thus the amount of angular momentum to be transferred, will depend on orbit distance (because the tide-generating force is, as I show in my article on The Tides, dependent on the inverse cube of the distance) and also on the difference between the spin speed of the Earth and the orbit speed of the Moon (because this is what determines how often a given point on the Earth passes through the tidal bulges, causing frictional loss). Unfortunately, the spin speed of the Earth depends on the orbit distance (as it is the change in spin speed which is causing the change in distance) as does the orbit speed of the Moon. We thus have a sort of "circular argument" problem: the recession rate depends on the distance but the distance depends on what the recession rate has been thus far. These inter-relationships have turned the problem from one that is solvable by simple arithmetic into one that needs to be tackled by a process of integration i.e. one in which the overall result of moving a large distance is found by performing calculations at each of a series of small distance-steps and summing the resultant values. This ensures that the linkages between the parameters only have a very small (and hopefully negligible) effect each time.
Conservation of Angular Momentum
Part of the problem can be tackled by a full analysis of the conservation of angular momentum in the Earth-Moon system. I have said previously that the spin angular momentum of the Earth is transferred to the orbital momentum of the Moon, but this is only an approximation because there are two other components to consider: the spin angular momentum of the Moon and the orbital momentum of the Earth. If at this point you exclaim that the Earth isn't orbiting anything then you clearly haven't read my article on The Tides! (or weren't paying attention). I show in that article that although it is normally stated that the Moon is orbiting the Earth, in fact they are both orbiting their common centre-of-gravity, called the barycentre. This means that the Earth does indeed possess orbital angular momentum - round the barycentre.
We know that the total angular momentum of the system must be constant, and this value can be calculated by summing the four components. The only variables involved in the sum are the distances of the centres of the Earth and the Moon from the barycentre and the spin and orbit periods of Earth and Moon. However, because the Moon's orbit is synchronous, its spin and orbit periods are the same and of course the Earth's orbit period round the barycentre must be the same as that of the Moon. Finally, the orbit period of the Moon depends only on its distance from the barycentre, and the barycentre distances depend only on the overall Earth-Moon distance (and the masses of both Earth and Moon, but these are constant). The expression for the total angular momentum thus has only two independent variables: the Earth-Moon distance and the spin speed of the Earth. By algebraically summing the expressions for each of the components and simplifying the resultant expression it is thus possible to derive an exact relationship between the spin speed of the Earth and the Earth-Moon distance.
Actually carrying out this process is exceedingly tedious, however, so I'm not going to detail all the steps here - definitely something to only be attempted with a large sheet of paper and plenty of time! The final answer is pleasingly simple though - the spin speed is equal to a constant, minus another constant times the square root of the distance, minus another constant divided by the square root of the cube of the distance. Calculation of the constants involves knowing just the mass & moment of inertia of both Earth & Moon and the gravitational constant (G). Once this is done, if one inserts current-day values for the spin speed and orbital distance one finds that the total angular momentum is 3.4415 x 1034 Kg m2/sec. Knowing this constant total value, we can now calculate the spin speed of the Earth for any Earth-Moon distance. Considering each component individually, we find that 81.96% of the total is contained in the orbit of the Moon and 17.03% in the spin of the Earth. The orbit of the Earth contributes almost all the final 1.01%, as the spin angular momentum of the Moon is negligible by comparison (just 0.000676% of the total) due to its relatively small mass and very slow rotation rate. These numbers show why the approximate treatment of the momentum transfer gives acceptable answers: the complication introduced by the orbital momentum of the Earth is quite small.
Tidal dissipation
We now need to determine the relationship between tidal dissipation and orbital distance. This is by no means as easy as it sounds, because of the way the tidal dissipation comes about. The dissipation is caused by viscous drag between the moving Earth and the almost-stationary tidal bulges and (in the case of the oceanic tides) friction between the tidal currents and the Earth's surface. Note that I said "almost stationary", because of course the bulges move round the Earth at the same speed as the Moon orbits. Note also that it is only the "form" of the bulges which is static, as the water or rock particles that constitute them at any given moment are constantly changing as the particles rotate with the Earth. It is this constant inter-change that causes the viscous drag.
The dissipation thus depends on the difference between the rotational speed of the Earth and the orbital speed of the Moon, as that is the effective speed at which objects on the Earth's surface interact with the bulges. This relationship can be represented by calculating the number of "tidal cycles" per year (where one cycle is high-low-high-low i.e. one "day's worth" of semi-diurnal tides). If Se is the rotational speed of the Earth and Sm is the orbital speed of the Moon [both in radians/sec] then the duration of a tidal cycle is 2 x pi / ( [Se - Sm] * 60 * 60) hrs and the number of tidal cycles in a year is given by dividing the duration into (365.2425 x 24). Currently, the duration is 24.84hrs and the number of cycles per year is 352.87. Both Se and Sm will change as the orbital distance changes, and so the number of tidal cycles per year will change also. We have already seen how the amount of energy transferred per year from the spin of the Earth to the orbit of the Moon can be calculated, so if we divide the current amount by the current number of tidal cycles per year this will give us the current energy transfer per tidal cycle. This is the starting point for further calculations - let's call this amount E0.
We now need to consider the fact that the size of the bulges (and thus the amount of dissipation per tidal cycle) will change as the Moon's orbital distance changes. This is a fairly straightforward relationship though - in the section "Evolution of the lunar orbit", above, I said that the magnitude of the tide-generating force depends on the inverse cube of the orbital distance. So, if E0 is the energy dissipated per cycle at the current distance, R0, the energy dissipated per cycle at another distance will be E = E0 x (R0/R)3. The total energy transfer per year is the amount per cycle times the number of cycles, which from the above expressions is [ (365.2425 x 24 x 60 x 60) / (2 x pi) ] x [Se - Sm] x E0 x (R0/R)3.
Conservation of Energy
The final brick in the wall is the calculation of how much the Moon's orbit will increase for a given amount of added energy. We already know that orbital kinetic energy equals 1/2 times G times the mass of both Moon and Earth divided by the orbit radius. Expressing this in symbolic form, E = 1/2 x G x Me x Mm / R. To find the change in E corresponding to a change in R (i.e. dE/dR, in mathematical terminology) we must differentiate this expression, which gives -1/2 x G x Me x Mm / R2. The change in orbital radius per Joule of energy is just the inverse of this, so dR/dE = 2 x R2 / (G x Me x Mm). [The minus sign just indicates that we are working in an environment where the bodies are attracting one another, so can be ignored for our purposes.]
The total energy transfer per year previously calculated can be written as dE/dT, so if we multiply this by dR/dE we will get dR/dT, which is the increase in orbital radius per year due to the given tidal dissipation: this is what we were originally trying to find (several paragraphs ago!). The full expression is rather long, so I shall combine all the constant factors such as G, Me, pi, R03, E0 etc. into one constant, which I shall call K. This gives the remarkably simple result that dR/dT = K x (Se - Sm) / R, an expression which nicely illustrates the "circular argument" point I made at the start of this section - the rate of change of radius is dependent on the value of the radius. It should not be forgotten, of course, that both Se and Sm are themselves also dependent on R, thus further complicating the issue.
If all this "energy loss per tidal cycle" and "proportional to R3" business seems a bit like I'm making it up as I'm going along, then all I can say is that the final result is (astonishingly!) precisely the expression given in the only Internet reference I could find that deals with this topic [4]. This reference gives no derivation though so I was unsure of its correctness. I did, however, find several references to tidal energy transfer calculations which included the (Se - Sm) term, which was encouraging and led me in the right direction. The "tidal cycles" treatment came from a reference I shall not give here, as it is full of errors such as forgetting that the number of cycles per year is affected by the Moon's speed as well as the Earth's. However, I worked through the method given there and, having corrected these errors, was astonished to find that the resultant answers were precisely as given by the expression in Ref.4. I thus carried out the algebraic analysis given above, to find that the two methods were exactly equivalent. I am thus happy that my analysis is correct.
The two methods do vary in one respect though: Ref.4 explicitly includes a term in the expression for dR/dT which accounts for the amount of tidal lag (the extent to which the tidal bulges are "ahead of" the Moon) but the tidal-cycles treatment does not. It's still there implicitly though, as part of the value of E0 - this means of course that it is assumed to be constant. In fact, Ref.4 also assumes it is constant and says as much in the description of the expression given. This assumption is, however, very unlikely to be true in practice. It is much more likely that the faster the Earth rotates the greater will be the amount that the tidal bulge is moved forward. This is supported by Stokes' Theorem which says that, in a non-turbulent situation, the drag force experienced by a body moving through a viscous medium is proportional to its speed. Whether this results in the bulge being dragged further forward or the tidal dissipation increasing (or some combination of the two), in each case the faster the Earth is rotating the greater will be the amount of energy and momentum transferred to the Moon. Taking my cue from the expression used to calculate the tidal dissipation (as mentioned in the page on Tide Heights), which uses the sine of the tidal phase lag, I have thus included a term which increases E0 by the ratio of the sine of the assumed lag at the given distance to the sine of the current tidal lag (the first element being found by multiplying the current lag by the ratio of the speed at the given distance to the current speed).
Graphical results
Having derived my final expression for dR/dT I was now ready to apply it to determine how the Moon's orbit would evolve. Using a spreadsheet, I calculated dR/dT for a series of orbital distances, each increasing by a small amount from the previous one. I then used each value to determine how long it would take the Moon to move between two successive orbital distances if it increased its orbit at the rate given by the value of dR/dT appropriate for this distance. These times were then summed, to give the time taken to move from the smallest to the largest orbital distance. The result is shown by this graph:-
 The x-axis is time in years from the present, with "now" at the zero point (shown by the yellow line): the past is to the left, the future to the right. The y-axis is orbital radius in metres: the current radius (3.844 x 108m) is where the graph crosses the yellow line. Each point on the line shows the time the corresponding radius would be achieved. One can thus see that the orbital radius would have been very small just less than 2 x 109yrs ago (1.936 x 109, in fact). Unfortunately, this is not what geological and paleontological studies of the Earth tell us, nor does it agree with the ages of the Moon-rocks brought back by the Apollo astronauts: the studies and the rocks all give an age for the Moon of about 4.5 x 109yrs. So what's gone wrong?
The x-axis is time in years from the present, with "now" at the zero point (shown by the yellow line): the past is to the left, the future to the right. The y-axis is orbital radius in metres: the current radius (3.844 x 108m) is where the graph crosses the yellow line. Each point on the line shows the time the corresponding radius would be achieved. One can thus see that the orbital radius would have been very small just less than 2 x 109yrs ago (1.936 x 109, in fact). Unfortunately, this is not what geological and paleontological studies of the Earth tell us, nor does it agree with the ages of the Moon-rocks brought back by the Apollo astronauts: the studies and the rocks all give an age for the Moon of about 4.5 x 109yrs. So what's gone wrong?
One could of course say "nothing" - it just shows that the Moon is much younger than scientists say it is and so there must be some error in the dating methods. However, the dates given by the geological and paleontological studies rely on fundamental physical processes such as radioactive decay, which are very unlikely to change with time, and are remarkably self-consistent. Furthermore, the theory I have explained in great detail above simply relies on basic physical laws - conservation of energy and conservation of momentum - and so is not likely to be seriously in error in a mathematical sense. However, the numerical results a theory gives depend on the parameters one supplies and herein lies the possibility of a "wrong" result.
Many of the parameters used in this theory are fixed quantities about which there can be no dispute (such as the mass of the Earth and the Gravitational Constant) but the amount of energy dissipated by tidal action is a "free" parameter i.e. its value is not determined by other inputs to the theory and so it can be chosen at will. I didn't use any old value of course, but one which was consistent with the current increase in the length of the day. Given that the ultimate answer is not in accord with observation however, we must conclude that the tidal dissipation (or, equivalently, the rate of slow-down of the Earth's spin) has not been constant throughout the life of the Earth-Moon system. This is not a "fudge" to get the theory to align with a result we would like to be true but rather an important result that tells us much about the Earth's history. If the tidal dissipation has changed over geological time then we must look for a reason: I shall do so later in this article.
Variable tidal dissipation
So, we may reasonably conclude that the reason why theory and observation do not agree lies in the value of the increase in the length of the day due to tidal dissipation which I used to calibrate the whole calculation. This determines the current value of dR/dT, which then determines the current amount of energy transferred per tidal cycle. The graph was generated using a constant value of 2.3milliseconds/century. If we set the increase to a constant 1.0milliseconds/century instead, we get a rather different situation - click/tap on the graph below to see it. The "very small radius" time has now increased to 4.443 x 109yrs, much closer to the usually accepted age of the Moon. However, the current value is definitely not 1.0msec/cy: this suggests that we need to find a way of reducing the overall value while retaining its well-accepted value in the current epoch i.e. we need to consider the possibility of changing the "constancy" of the slow-down rate rather than the value.
 The first observation concerning constancy is that until it had cooled sufficiently for it to retain liquid water, the Earth could not have had any oceans - and if there are no oceans there can be no oceanic tidal dissipation. Evidence gleaned from the ages of rock types which would have needed water for them to form indicates that there were certainly extensive bodies of water at about 3.8 x 109yrs before the current epoch, and probably as early as 4.0 x 109yrs. Before this time however, there can have been no oceanic tidal dissipation. Tides in the solid body of the Earth would still have been present of course but these are 22 times less effective in dissipating energy than oceanic tides. This would clearly result in a much slower increase in length of day due to the much lower loss of rotational energy. Secondly, as I showed in my article on The Tides, we are currently in a time when the presence of the continents inhibits the "standing-wave" type of tides described by the Dynamic Theory of tides and also when the natural circulation periods of the oceans are almost perfectly matched to the frequency of the tide-generating force. The resonances that this produces result in a much greater dissipation of energy than if there was a mis-match or if standing-wave tides were possible. It is thus reasonable to assume that the current increase in the length of the day is considerably higher than the typical value over geological time.
The first observation concerning constancy is that until it had cooled sufficiently for it to retain liquid water, the Earth could not have had any oceans - and if there are no oceans there can be no oceanic tidal dissipation. Evidence gleaned from the ages of rock types which would have needed water for them to form indicates that there were certainly extensive bodies of water at about 3.8 x 109yrs before the current epoch, and probably as early as 4.0 x 109yrs. Before this time however, there can have been no oceanic tidal dissipation. Tides in the solid body of the Earth would still have been present of course but these are 22 times less effective in dissipating energy than oceanic tides. This would clearly result in a much slower increase in length of day due to the much lower loss of rotational energy. Secondly, as I showed in my article on The Tides, we are currently in a time when the presence of the continents inhibits the "standing-wave" type of tides described by the Dynamic Theory of tides and also when the natural circulation periods of the oceans are almost perfectly matched to the frequency of the tide-generating force. The resonances that this produces result in a much greater dissipation of energy than if there was a mis-match or if standing-wave tides were possible. It is thus reasonable to assume that the current increase in the length of the day is considerably higher than the typical value over geological time.
I thus further modified my model to include explicit allowance for the lag angle and the effectiveness of the tides. This latter is given by the k2 Love Number which I mentioned in the Tide Heights page of my article on The Tides: it is a measure of the height of the tidal bulge. While not mentioned in Ref.4, the references I found to calculations involving the (Se - Sm) term in the context of tidal energy transfer (as mentioned above) did indeed incorporate k2 as one of the factors in their constant term. I thus felt entirely justified in including it as part of my E0 term.
Having set up the new expressions, in the period from the distant past up to 4.1 x 109yrs before the present I used the lag and k2 values relevant to the solid Earth rather than those relating to an Earth with oceans. I smoothly increased these values to those used for the majority of the graph over the period from 4.1 x 109 to 3.75 x 109yrs before the present to simulate the appearance of the oceans. I set the lag angle for the majority of geological time to a constant value (which I could then change), with the Love Number set to that for "Earth plus oceans". Finally, I set the lag angle for the period around the current epoch to the current value and smoothed the change to and from the "majority" lag angle value to the "current" value to simulate the changes in the continents and oceans. I set the calibration value for the current length-of-day increase at 2.3msec/cy, its correct value. I then determined the value of the tidal lag used for the majority of geological time which would produce a graph whose "very small orbital radius" date was the same as that given by the graph using constant parameters and a value of 1.0msec/cy for the increase in day-length.
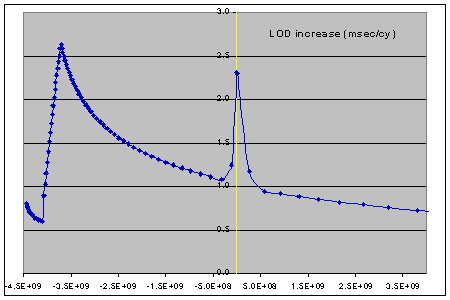
 | The result of all these modifications can be seen by clicking/tapping on the graph to the left, which is the one above repeated for convenience. The new blue graph is clearly a much better match to the "constant 1.0msec/yr" graph than the old one: in particular, the consequence of there being no oceans early on is quite obvious (the slight variation due to the current continental situation is not so apparent however). I thus feel confident in saying that the types of modification I have introduced to the theory are highly likely to reflect actual processes which occured in the early development of the Earth. |
The majority tidal lag value turned out to be 1.28deg (compared with the current value of 2.9deg). This is the value before taking into account the change in rotation speed, however. I thus calculated the same scaling factor as before (the one involving sines) at each calculated point but, as it seemed most instructive to show the result as a "length-of-day increase" value rather than as a lag value, I applied it to the 2.3msec/cy number corresponding to a lag of 2.9deg rather than the lag itself. This is valid because we are using the lag (and k2) to calculate energy dissipated and the change in length-of-day is proportional to the energy dissipated. The result is shown by the next graph:-
 | The five phases of the evolution of the Moon's orbit can be clearly seen. Starting at the far left, there are no oceans on the Earth and so little dissipation (despite the high spin-speed) and so the increase in length-of-day is minimal. The oceans then begin to form and the dissipation increases markedly: the maximum length-of-day increase actually happens at this point (2.63msec/cy). The value falls away as the spin-speed decreases but then moves up again for a while as the resonant effects I have assumed to be peculiar to the current epoch kick in. Finally, as the continents re-arrange themselves again, the increase reverts to its slowly-decreasing long term behaviour. If we consider only those points representing the period from the formation of the Moon to the present epoch, the average length-of-day increase (averaged by orbital radius) is 1.60msec/cy. Averaged by time it is 1.52msec/cy, which is consistent with the value of 1.55msec/cy needed to decrease the Earth's rotational period from its value 4.443 x 109yrs ago to its value now. |
One might raise the objection here that the distinct peak at the current epoch looks rather artificial - it is surely unlikely that the length-of-day increase changed in exactly this way. I thought so too, so I carried out further investigations into the reasons why tidal dissipation might change over time.
Further complications
As mentioned almost at the beginning of this page, the other commonly-quoted figure for the increase in the length of the day, 1.7 milliseconds per century, is the actual current net rate of increase in the length of the day. This is less than the 2.3msec/cy produced by tidal dissipation because of such factors as the slight decrease in the Earth's moment of inertia caused by its change in shape due to the removal of the ice burden after the last Ice Age, which will cause the Earth to spin slightly faster. The trade-off between moment of intertia and spin speed is a non-dissipative process though, as it depends on conservation of energy, and so it does not directly affect the Earth/Moon distance. Any second-order effects (due to the decrease in moment of inertia also affecting the dissipative part of the situation and the increase in spin speed affecting the tidal friction) will be extremely small because of the very small time interval (geologically speaking) over which they have occurred - of the order of just 10,000yrs. Even if we say that the interval is a full million years, so the difference between the tide-induced and net figures is 6 seconds, the change in moment of inertia necessary to produce this increase in spin period is just -0.014% and the change in spin speed itself is a mere +0.007%. Safe to ignore effects of this magnitude, I think. On the other hand, it is generally accepted that Ice Ages have happened at intervals of something like 100,000yrs for at least the last million years, due to periodicities in the variation of the eccentricity, obliquity & precession of the Earth's orbit. If this behaviour is typical of the majority of the history of the Earth/Moon system then we must consider whether the second-order effects could make a noticeable cumulative difference.
The most likely answer is that, because Ice Age cycles are indeed cycles, their total net effect is very small. The decrease in moment of inertia plus increase in spin speed we are currently experiencing is simply compensating for the reverse effects that happened when the Earth went into the most recent Ice Age. There will thus be periodic, but extremely small, fluctuations in the Moon's recession caused by Ice Ages but no secular change. The changes in sea-level brought about by the freezing and melting of the oceans during Ice Age cycles may have a more significant influence however, as this has the potential to change the tidal friction, which is a dissipative effect and so could produce a secular change. Tidal friction is greatest in shallow seas but of course shallow seas will produce smaller tidal bulges, which exert a lesser torque on the Moon, making the overall outcome very hard to model.
About the only friction-varying effect about which anything definite can be said is the change in position of the Earth's landmasses due to continental drift. The presumption that we are currently in a high-friction conformation seems fairly well established (based on the anomalously high value for the length-of-day increase). Current theories of continental drift indicate that the several large and well-spaced continents we have today were formed from the break-up of a super-continent called Pangea about 225 million years ago. Before the breakup, however, the "super-continent" was in fact the usual conformation. The following animation (courtesy of University of California Museum of Paleontology) shows this well - click or tap on it to start or restart, hit "Escape" to stop. The number at bottom right of the map indicates millions of years before now. The scale shows the geological age this corresponds to.
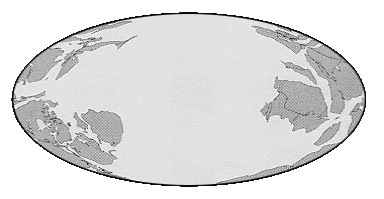

When interpreting the map, don't forget that it is an "unwrapped" representation of the Earth's surface i.e. the left and right edges are in fact adjoining. The first frame thus shows one large (but somewhat fragmented) landmass, not two smaller ones.
Large landmasses affect the tidal dissipation in two main ways. Firstly, because one large continent has much less coastline than two smaller ones covering the same area, it will produce much less tidal dissipation than them (because dissipation mainly occurs in shallow water). Secondly, the large areas of ocean that lie between concentrated landmasses allow tidal currents to flow with little obstruction, and therefore little dissipation. It is thus reasonable to assume that "Pangea-style" conformations produce far less tidal dissipation than the "multi-continent" arrangement we have at present, and therefore have lower values of length-of-day increase and thus lunar recession. The animation only covers 20% of the history of an Earth with oceans though, so we cannot be sure what happened before then. However, as long as the current situation is not simply unique, we might guess that multiple continents are a conformation that happens periodically. We could thus perhaps postulate a cyclical switch from low to high dissipation conformations with an interval of about 0.75 x 109years (i.e. the time-span of the animation) between low and high. To see what effect this might have, I modified my model to incorporate this scheme by adding an amount to the tidal lag angle for even multiples of 0.75 x 109years before the present and subtracting for odd multiples. Some of the "in-between" points were also increased/decreased by fractions of the set amount, to avoid abrupt changes. The result is shown on the next graph:-
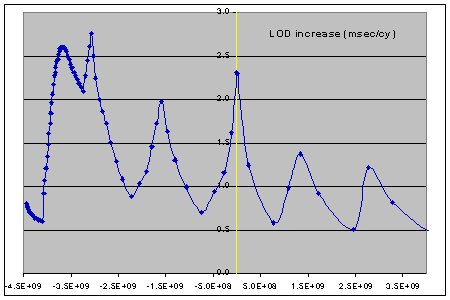 | The 1.5 x 109yr periodicity is obvious, as is the fact that the amount I added/subtracted was rather less than the difference between the mean value and the current value. In fact, I used a value of 0.6 as this gave a good "visual" impression of the effect. What the real value might be is impossible to tell, of course, as is what would happen at the peak of the original graph. Here the maximum calculated dissipation comes exactly at a time when the continents should be in a low-dissipation conformation, but it is also the time when the oceans have only just formed and when the effect of the very large tides crashing against whatever continents did exist would have been pretty huge anyway. I have thus just added in a small effect, which acts to "smooth off" the peak. Under these assumptions, the average length-of-day increase from the formation of the Moon up to the present day (averaged by orbital radius) is 1.71msec/cy and the majority tidal lag angle is 1.38deg. The length-of-day increase averaged by time stays the same, at 1.52msec/cy, as one might have expected. |
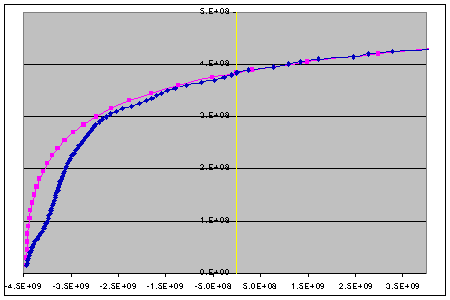 | Thus, while the new graph gives some idea of what might happen (and is certainly more plausible than the "single peak" version given earlier), it's not really possible to show other than a reasonably informed guess. Fortunately, detailed work has been done on this problem [5] and the conclusion is that the effects of continental drift do not cause a problem with the modelled 4.5 x 109yr timescale for the evolution of the Earth/Moon system. The lack of dramatic change in the radius vs. time graph (left) would seem to support this view. Rather surprisingly, despite the huge oscillations in the length-of-day graph this one just rises up a bit in the middle (corresponding to the peak at 3 x 109yrs) and acquires a few minor "wiggles": click or tap the image to compare the two cases. |
Conclusions
So, far from simply applying a "fudge" to get things to fit, we have derived significant new information from the fact that the original graph did not accord with actual observational evidence. The need to build in the effect of the period when the Earth had no oceans is seen to be important, as is the realisation that dissipation will be high initially but will then reduce considerably as the Earth's spin-speed slowly decreases. Finally, the contribution to the variation in tidal dissipation from changing continental land-mass dispositions becomes the critical factor in achieving a lower average dissipation while allowing high values at certain epochs (such as the present).
And now a couple of topics associated with the Recession of the Moon, before we get to the References.

The Extinction of Total Solar Eclipses
Having derived a reasonable model for the lunar recession, it can be used to help answer an often-asked question - when will total solar eclipses become impossible? A calculation of this sort was attempted by the famous mathematical astronomer Jean Meeus in his book 'More Mathematical Astronomy Morsels', using the current value of lunar recession - 3.8cm/yr. He came up with the answer "in 1210 million years", but did concede that constant recession at today's value was "doubtful". Given that my studies indicated that this assumption was not just doubtful but definitely false, I decided to see what answer my model would give. Unfortunately, as with so many analyses of this sort, things soon became more complicated so I've moved the discussion to a subsidiary page - click here to read it.
Summary
Taking all factors into account, we can say that for the first 2.8 billion years of the Moon's existence all eclipses would have been total, due to the large apparent size of the Moon caused by its close proximity to the Earth. The duration of these eclipses would have been much longer than equivalent ones now because the Moon's increased size and the Earth's quicker rotation will more than compensate for the Moon's faster orbital speed. For example, a "maximum-length" eclipse (i.e. one occurring exactly at perigee and aphelion), which would last 7mins 32sec in the current epoch, would have lasted 13min 12sec at a time 2.5 billion years before the present. Early eclipses would also have been visible over a much greater area - the path width in the example would have been almost 3 times that of the "modern" eclipse. Eventually though, the decrease in apparent size of the Moon due to its recession from the Earth would have allowed for the possibility of annular eclipses, beginning at around 1.69 billion years before the present and becoming possible at any value of the Earth's orbital eccentricity around 1.20 billion years ago.
Looking into the future, the increasing size of the Sun quickly becomes the dominant factor, maybe resulting in total eclipses starting to become impossible in just 650 million years. It is however certain that after about 1.17 billion years only annular eclipses will be possible, even at favourable values of orbital eccentricity, though the total number of eclipses overall will slightly increase [I must make it clear at this point that the close agreement between this figure and Meeus' estimate is purely coincidental, as his calculation embodied a number of incorrect assumptions - go back and read my full discussion if you're not convinced!]. Eclipses will steadily get less and less dramatic as the Sun continues to expand, until the inner planets of the Solar System meet a fiery end as the Sun turns into a Red Giant star. Sic transit gloria mundi, one might say.

Rotational and Orbital periods
I have said that the Earth's period of rotation on its axis and the Moon's orbital period round the Earth will both change as the Moon recedes, so I thought it would be interesting to show a graph of this behaviour:-
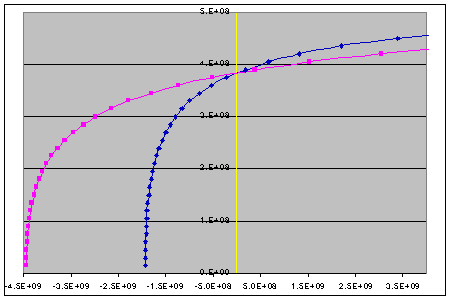
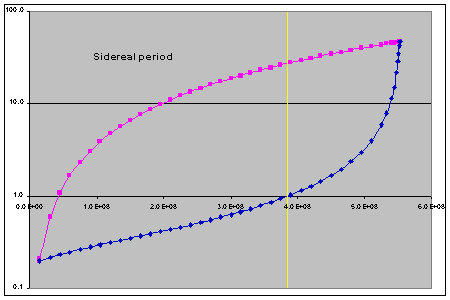 The blue line gives the Earth's period, the pink one the Moon's (both read from the y-axis), for values of Earth-Moon distance on the x-axis. Both periods are in sidereal days i.e. relative to the fixed stars. The yellow vertical line indicates "now". Note that the y-axis scale is logarithmic, by the way. Note also that this graph can't be compared to the length-of-day increase graph shown earlier as this one simply plots period against orbital radius without taking into account how and at what rate the radius increases. In other words it is basically just a representation of the effect of conservation of angular momentum taken together with Kepler's Third Law and Newton's Law of Gravitation.
The blue line gives the Earth's period, the pink one the Moon's (both read from the y-axis), for values of Earth-Moon distance on the x-axis. Both periods are in sidereal days i.e. relative to the fixed stars. The yellow vertical line indicates "now". Note that the y-axis scale is logarithmic, by the way. Note also that this graph can't be compared to the length-of-day increase graph shown earlier as this one simply plots period against orbital radius without taking into account how and at what rate the radius increases. In other words it is basically just a representation of the effect of conservation of angular momentum taken together with Kepler's Third Law and Newton's Law of Gravitation.
It can be seen that there are two points at which the periods are the same i.e. where the Earth and Moon are rotating synchronously. At the bottom-left point the Moon's orbital radius is 14,561.1 kilometres and the period is 4hrs 50mins, and at the top-right point the values are 552,852.7km and 47days 3hrs. The first synchronous point is somewhat theoretical, therefore, as it is inside the Roche Limit for Earth (the orbit radius within which an orbiting body will be destroyed by tidal forces) - 18,470km. This is just as well of course, because there can be no tidal acceleration on the Moon if it and the Earth are rotating/orbiting at the same speed [because (Se - Sm) will then be zero] so the whole recession process would never have got under way! The existence of this point is therefore simply telling us that around this period the Moon was very close to the Earth. Current theories of lunar formation say that the Moon came into being when a planet about the size of Mars (usually called Theia) which had formed in the same orbit as the Earth collided with it. Some material was lost to space, some accreted onto the Earth and the rest gathered together to form the Moon - at a distance greater than the Roche Limit, of course. I think this would count as being "very close to the Earth" however!
The other synchronous point is also of theoretical interest only, but for a rather different reason. Extending the radius/time calculations forward we find that it will take another 4.27 x 1010yrs for the Moon's orbit radius to exceed 500,000km. To reach the full 552,852.7km would take a theoretically infinite amount of time because the limit is approached more and more slowly for each additional kilometre. However, even 4.27 x 1010yrs is almost 10 times the present age of the Solar System. We may thus say that, in practice, the Earth and Moon will never achieve synchronous orbit.

| References (Return to text) |
| [1] | This reference is to another of my Astronomical Theory articles, in which I give a comprehensive description of the physical mechanisms which produce tides on co-orbiting bodies and then extend this to the particular case of the tides induced on the Earth by the Moon and Sun. Within this, I calculate the theoretical height of such tides. Given the close connection between tidal processes on the Earth and the recession of the Moon, I have need to refer to this other article on a number of occasions. |
| [2] | Semi-diurnal and diurnal tidal dissipation from TOPEX/POSEIDON altimetry - G.Egbert & R.Ray. Geophysical Research Letters Vol 30 No.17. [Warning - was slow to download when I did so!] |
| [3] | Ibid. Table 1, page 2. |
| [4] | Astronomy Answers: Evolution of the Lunar Orbit - Dr Louis Strous |
| [5] | A Stochastic Model of the Earth-Moon Tidal Evolution Accounting for Cyclic Variations of Resonant Properties of the Ocean: an Asymptotic Solution - Kagan, B. A. & Maslova, N. B. Earth, Moon, and Planets Journal, Volume 66, Issue 2, pp.173-188 |
 Although those who have read my article on The Tides[1] will know that this terminology is not strictly accurate, the Moon-distance increase is normally explained via the agency of the tidal bulges (both in the oceans and in the solid body of the Earth) which, as shown by this diagram, are pulled forward of the Moon by frictional drag as the Earth rotates in the direction of the yellow arrow. The gravitational attraction of the nearer bulge for the Moon, shown by the green arrow, is therefore in front of the centre-to-centre line and so would be in such a direction as to have a component along the Moon's orbit. This would speed it up, leading to an increase in the size of its orbit [If you are not clear why this should be so, my article on Orbital Dynamics explains the physics of this situation]. The energy required to achieve this speed-up is taken from the rotational energy of the Earth, thus accounting for the slow-down in its spin rate. In addition, dissipation of additional energy by the tides enables sufficient angular momentum to be transferred to the orbit of the Moon from the spin of the Earth as this gets steadily slower. In principle, therefore, one ought to be able to calculate the rates of recession and slow-down due to the transfer of energy and momentum by working out the torque exerted on the Moon by the bulges.
Although those who have read my article on The Tides[1] will know that this terminology is not strictly accurate, the Moon-distance increase is normally explained via the agency of the tidal bulges (both in the oceans and in the solid body of the Earth) which, as shown by this diagram, are pulled forward of the Moon by frictional drag as the Earth rotates in the direction of the yellow arrow. The gravitational attraction of the nearer bulge for the Moon, shown by the green arrow, is therefore in front of the centre-to-centre line and so would be in such a direction as to have a component along the Moon's orbit. This would speed it up, leading to an increase in the size of its orbit [If you are not clear why this should be so, my article on Orbital Dynamics explains the physics of this situation]. The energy required to achieve this speed-up is taken from the rotational energy of the Earth, thus accounting for the slow-down in its spin rate. In addition, dissipation of additional energy by the tides enables sufficient angular momentum to be transferred to the orbit of the Moon from the spin of the Earth as this gets steadily slower. In principle, therefore, one ought to be able to calculate the rates of recession and slow-down due to the transfer of energy and momentum by working out the torque exerted on the Moon by the bulges. The x-axis is time in years from the present, with "now" at the zero point (shown by the yellow line): the past is to the left, the future to the right. The y-axis is orbital radius in metres: the current radius (3.844 x 10
The x-axis is time in years from the present, with "now" at the zero point (shown by the yellow line): the past is to the left, the future to the right. The y-axis is orbital radius in metres: the current radius (3.844 x 10





 The blue line gives the Earth's period, the pink one the Moon's (both read from the y-axis), for values of Earth-Moon distance on the x-axis. Both periods are in sidereal days i.e. relative to the fixed stars. The yellow vertical line indicates "now". Note that the y-axis scale is logarithmic, by the way. Note also that this graph can't be compared to the length-of-day increase graph shown earlier as this one simply plots period against orbital radius without taking into account how and at what rate the radius increases. In other words it is basically just a representation of the effect of conservation of angular momentum taken together with Kepler's Third Law and Newton's Law of Gravitation.
The blue line gives the Earth's period, the pink one the Moon's (both read from the y-axis), for values of Earth-Moon distance on the x-axis. Both periods are in sidereal days i.e. relative to the fixed stars. The yellow vertical line indicates "now". Note that the y-axis scale is logarithmic, by the way. Note also that this graph can't be compared to the length-of-day increase graph shown earlier as this one simply plots period against orbital radius without taking into account how and at what rate the radius increases. In other words it is basically just a representation of the effect of conservation of angular momentum taken together with Kepler's Third Law and Newton's Law of Gravitation.