is the angle between them, the first definition gives us (AxBx) + (AyBy) + (AzBz) and the second gives us |A| |B| cos. By combining the two forms we get our result:-On this page I will explore in more detail how one may calculate the angle between two arbitrary vectors, in order to find the angle between the Earth-Moon line and the Earth's spin angular velocity vector. Having found this angle, the calculation of the Potential Energy of the system may resume.
The definition of a vector is a quantity with both magnitude and direction. In graphical terms, if the vector is represented by an arrow of definite length pointing in a definite direction, the magnitude of the vector is the length of the arrow and the direction of the vector is of course the pointing direction of the arrow. The magnitude and direction can be broken down into components in the x, y & z-directions of a set of Cartesian co-ordinates, and one can represent the components by listing the expressions for them in sequence within brackets, thus - A = (Ax, Ay, Az) - which means that the vector A can be constructed from the components Ax, Ay & Az in the x, y & z-directions respectively. This form of representation enables vectors to be manipulated according to sets of rules to produce useful results, such as the one we are looking for.
To find the angle between two arbitrary vectors we can use the two definitions of the "scalar product" of two vectors. The scalar product is found on the one hand by adding together the results of multiplying the corresponding components of each vector together and on the other by multiplying the cosine of the angle between them by the magnitudes of each vector. Thus, if A and B are both vectors and is the angle between them, the first definition gives us (AxBx) + (AyBy) + (AzBz) and the second gives us |A| |B| cos. By combining the two forms we get our result:-
cos = { (AxBx) + (AyBy) + (AzBz) } / { |A| |B| }
In the case of the Earth-Sun line, the spin angular velocity has no dependence on 
, which results in there being a zero x-component. Also, the line is always in the global x-y plane and so has no component in the z-direction. Simple trigonometry will thus show us that the velocity and radius vectors are:-
We can thus see that when we apply the scalar product equation, the x and z components will produce a zero result and so the angle between the vectors will be formed only from the y-components of the two, resulting in the simple result cos 
= sinsin 
, as stated on the main page.
The tilt of the Moon's orbit means the Earth-Moon line has a z-component and, likewise, the dependence on means the spin angular velocity has a non-zero x-component.
To find the z-component of the Earth-Moon line, we must invoke a theorem of spherical geometry known as Napier's Second Rule, which can be illustrated by the next diagram.
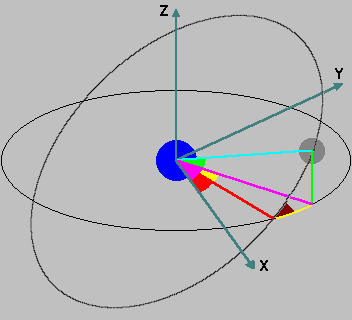The diagram is similar to the one showing the Earth-Sun situation on the main page, but with the Sun removed and the Moon, together with its inclined orbit, added. If we refer to the small [curved] triangle formed by the yellow, green and black lines just below the Moon, the Rule says that the sine of the angle corresponding to the yellow arc (i.e. the yellow angle) is equal to the tangent of the angle corresponding to the green arc (i.e. the green angle) divided by the tangent of the angle in brown (which is the inclination of the Moon's orbit). Clearly, the yellow angle is equal to the purple angle minus the red angle. The purple angle is the counterpart of in the Earth-Sun case, so we can call it 
. The red angle is the angle between the axis of the Moon's orbit and the co-ordinate x-axis - we will call it 
[Note that, because the Moon's orbital precession is in the opposite direction to its orbit rotation, decreases with time]. Napier's Rule thus says that sin( - ) = tan(green angle) / tan(inclination).
Now, simple trigonometry tells us that the tangent of the green angle is [very nearly] equal to the length of the green line divided by the length of the light blue line. The light blue line is just the Moon's orbital radius, 
, and the green line is the length we have been trying to find - the z-component of the Earth-Moon line. So, re-arranging the expression a bit,
Z = { tan(inclination) * sin( - ) }.
We can make a final simplification by noting that, as long as an angle is expressed in radians and is quite small, its tangent is very nearly equal to its own value i.e. in our case tan(inclination) = inclination: we shall call this value 
. The final expression is therefore Z = { * sin( - ) }. Given that the x and y-components will be unchanged by the orbit inclination, the component representation of the Earth-Moon line is:-
[ A note on my use of "very nearly" in the above derivation would seem to be in order here. The first usage hinges round the fact that "the length of the green line" has a number of possible interpretations, three of which are of relevance to the current situation. Firstly, its true length is found by recognising that it is, in fact, an arc not a straight line and that the light blue and purple lines are actually the same length (because all points on either of the orbit ellipses actually sit on the surface of a sphere that has the Earth at its centre). The true length is therefore given by 2 * pi * * (green angle) / 360. Given that there are 2 * pi radians in 360 degrees, this expression reduces to the value of the green angle in radians times . The next interpretion is to assume that the angle between the light blue line and the green line is 90deg, as I did above. This allows us to involve the tangent of the green angle, which appears in Napier's Rule. The final interpretation of use is to assume that the green line is perpendicular to the x-y plane - this will give us the true value of the z-component of the Earth-Moon line, and it's equal to the sine of the green angle times .
We thus have three possible lengths for the green line, which are (ignoring the factor) the green angle expressed in radians, the tangent of the green angle and the sine of the green angle. It is clear from the geometry of the situation that the green angle can never be greater that the inclination of the Moon's orbit (the brown angle), the average value of which is 5.16deg. The maximum relative lengths of the green line under the three interpretations are thus 0.09006 [the true length of the line]; 0.09030 [the value which allows Napier's Rule to be used], and 0.08994 [the true length of the z-component] respectively. We thus see that the Napier's Rule version differs from the true length by just +0.27%, the true z-component version differs by a mere -0.13% and the Napier's Rule and true z-component versions differ by only 0.4% from each other. It is thus clear that whichever version we use the value is going to be "good enough", bearing in mind the other approximations made during the derivation.
The above example has already shown that, in the small angle regime, the tangent of the angle is very close to the value of the angle in radians, which covers my second use of "very nearly". ]
We must now turn our attention to the components of the spin angular velocity. The tilt of the Moon's orbit means that both the x and y-components have a dependence on , which means the x-component of the spin angular velocity is non-zero.
If we ignore the 
factor, with = 0deg (i.e. when the velocity vector points in the +y direction), simple trigonometry tells us that the x-component will be 0, the y-component will be sin and the z-component will be cos. With = 90deg (i.e. when the vector points in the -x direction), the x-component will be -sin, the y-component will be 0 and the z-component will still be cos. Continuing this logic for equal to 180deg and 270deg might lead one to conclude that the x-component had a dependency on sin, the y-component had a dependency on cos and the z-component had no dependency on - this conclusion would, in fact, be correct. The component representation of the spin angular velocity vector is therefore:-
In our case, the magnitudes of the two vectors are (by definition) simply and . After performing the multiplications of the components, and using the identity sin(A-B) = sinA cosB - cosA sinB to sort out the result, we eventually find that:-
It can be seen that with = 0 and no dependency on this expression reduces to the form used in the Earth-Sun case.
So, now that an expression for cos 
has been found we can return to the main page to continue the construction of the Potential Energy part of the Lagrangian for the Earth-Moon system.
